12 câu hỏi
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
\(\left( { - \infty ;2} \right)\).
\(\left( { - 2;\, + \infty } \right)\).
\[\left( {0;\, + \infty } \right)\].
\[\left( { - 2;\,0} \right)\].
Giá trị cực tiểu của hàm số đã cho là
\[ - 2\].
\[0\].
\[2\].
\[6\].
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \(\left[ { - 1;\,3} \right]\) và có đồ thị như hình dưới đây.
![Cho hàm số y = f(x) liên tục trên đoạn [-1; 3] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid289-1727780211.png)
Phát biểu nào sau đây là đúng?
Hàm số đã cho không có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn \(\left[ { - 1;\,3} \right]\).
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 1;\,3} \right]\) bằng \[3\].
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 1;\,3} \right]\) bằng \[2\].
Hàm số đã cho đạt giá trị lớn nhất tại \(x = 0\).
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
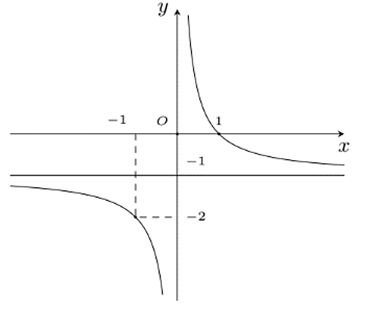
Phát biểu nào sau đây là đúng?
Đồ thị hàm số đã cho có đường tiệm cận đứng \(x = - 1\), đường tiệm cận ngang \(y = 0\).
Đồ thị hàm số đã cho có đường tiệm cận đứng \(x = - 1\), đường tiệm cận ngang \(y = - 1\).
Đồ thị hàm số đã cho có đường tiệm cận đứng \(x = 0\), đường tiệm cận ngang\(y = 0\).
Đồ thị hàm số đã cho có đường tiệm cận đứng \(x = 0\), đường tiệm cận ngang \(y = - 1\).
Tiệm cận xiên của đồ thị hàm số \(y = x + 4 - \frac{{10}}{{x + 2}}\) là đường thẳng
\(y = x + 4\).
\(y = x + 2\).
\(y = - x - 4\).
\(y = - x - 2\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây.

Tâm đối xứng của đồ thị hàm số có tọa độ là
\(\left( {2;\,2} \right)\).
\(\left( { - 2;\, - 2} \right)\).
\(\left( { - 2;\,2} \right)\).
\(\left( {2;\, - 2} \right)\).
Cho hình hộp \(ABCD.A'B'C'D'\).
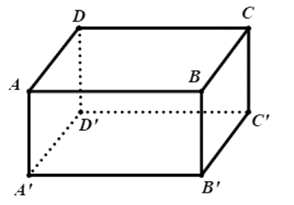
Tổng \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) bằng vectơ nào sau đây?
\(\overrightarrow {AC} \).
\(\overrightarrow {AC'} \).
\(\overrightarrow {A'C'} \).
\(\overrightarrow {A'C} \).
Cho hàm số \(y = x - \frac{1}{x}\). Phát biểu nào sau đây là sai?
Hàm số đã cho có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\).
Hàm số đã cho nghịch biến trên \(\mathbb{R}\).
Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).
Hàm số đã cho đồng biến trên khoảng \(\left( {0;\, + \infty } \right)\).
Giá trị nhỏ nhất của hàm số \[y = \frac{{{x^2} + 3}}{{x - 1}}\] trên đoạn \(\left[ {2;\,\,4} \right]\) bằng
\(3\).
\(\frac{{19}}{3}\).
\(6\).
\(7\).
Đường cong trong hình dưới là đồ thị của hàm số nào trong bốn hàm số sau đây?
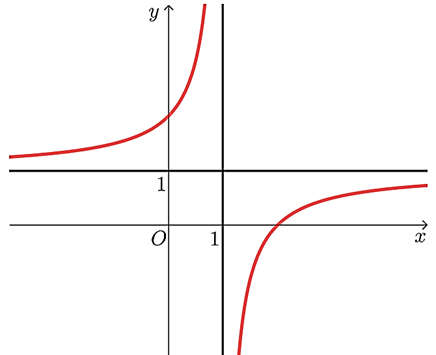
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = \frac{{x - 2}}{{x - 1}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{x - 3}}{{x - 2}}\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ dưới đây.
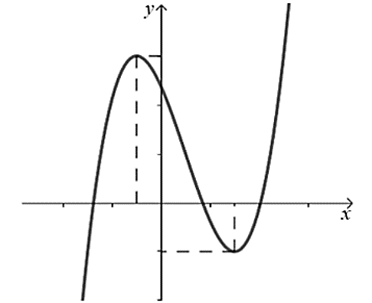
Khẳng định nào sau đây là đúng?
\(a > 0,\,b > 0,\,c > 0,\,d > 0\).
\(a > 0,\,b < 0,\,c > 0,\,d < 0\).
\(a > 0,\,b > 0,\,c < 0,\,d > 0\).
\(a > 0,\,b < 0,\,c < 0,\,d > 0\).
Cho hai vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) thỏa mãn: \(\left| {\overrightarrow a } \right| = 4;\,\,\left| {\overrightarrow b } \right| = 3;\,\,\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi \(\alpha \) là góc giữa hai vectơ \(\overrightarrow a ,\,\,\overrightarrow b \). Chọn khẳng định đúng trong các khẳng định sau.
\(\cos \alpha = \frac{3}{8}\).
\(\alpha = 30^\circ \).
\(\cos \alpha = \frac{1}{3}\).
\(\alpha = 60^\circ \).
