11 câu hỏi
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\[3{x^2} + y = 1\].
\[3x + y--z = 0\].
\(\frac{1}{x} + 3y = 2.\)
\[3x--\frac{1}{2}y = 0.\]
Phương trình \[4y - 3x = 5\] nhận cặp số nào sau đây làm nghiệm?
\[\left( {1\,;\,\,2} \right)\].
\[\left( {2\,;\,\,1} \right)\].
\[\left( {2\,;\,\,2} \right)\].
\(\left( {1\,;\,\,1} \right).\)
Trên mặt phẳng tọa độ \[Oxy,\] cho các điểm \[A\left( {3\,;\,\, - 1} \right)\], \[B\left( {0; - 2} \right)\], \[C\left( {6;0\,} \right)\], \[D\left( { - 1\,;\,\,2} \right).\] Điểm nào không thuộc đường thẳng \(\frac{1}{2}x - \frac{3}{2}y = 3\)?
Điểm \[A\].
Điểm \[B\].
Điểm \[C\].
Điểm \[D\].
Hệ phương trình nào có cùng cặp nghiệm với hệ phương trình \[\left\{ \begin{array}{l}5x + 4y = 1\\3x - 2y = 5\end{array} \right.\] ?
\[\left\{ \begin{array}{l}3x + 2y = 1\\x + y = 0\end{array} \right.\].
\[\left\{ \begin{array}{l}3x + 2y = 1\\x - y = 0\end{array} \right.\].
\[\left\{ \begin{array}{l}3x - 2y = 1\\x + y = 0\end{array} \right.\].
\[\left\{ \begin{array}{l}3x - 2y = 1\\x - y = 0\end{array} \right..\]
Điều kiện xác định của phương trình \(\frac{1}{{x + 2}} - 3 = \frac{2}{{x - 2}}\) là
\[x \ne - 2;{\rm{ }}x \ne 2\].
\[x \ne 2;{\rm{ }}x \ne 1\].
\[x \ne 1;{\rm{ }}x \ne --2\].
\[x \ne 1;{\rm{ }}x \ne \pm 3\].
Phát biểu “\(a\) không nhỏ hơn \(b\)” được biểu diễn bằng bất đẳng thức nào dưới đây?
\(a < b.\)
\(a \ge b.\)
\(a \le b.\)
\(a > b.\)
Với \(a > b\), chọn khẳng định sai trong các khẳng định dưới đây ?
\(a - 2 > b - 2.\)
\( - 5a > - 5b.\)
\(2a + 3 > 2b + 3.\)
\(10 - 4a < 10 - 4b.\)
Bất phương trình nào sau đây không phải là bất phương trình bậc nhất một ẩn?
\[\frac{1}{2}x + 2 < 0\].
>
\[2x + 1 - 2\left( {x + 3} \right) > 0\].
\[3x - 1 \ge 1\].
\[x + \frac{1}{3} \le 0\].
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha \). Tỉ số \(\frac{{HA}}{{HB}}\) bằng
\(\sin \alpha \).
\[\cos \alpha \].
\(\tan \alpha \).
\(\cot \alpha \).
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH.\) Biết \(AB = 2,5\), \(BH = 1,5.\) Số đo góc \(\widehat B\) là
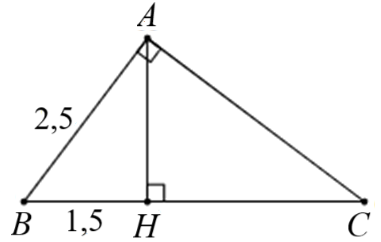
\(\widehat B = 30^\circ .\)
\(\widehat B = 53^\circ 1'.\)
\(\widehat B = 35^\circ 1'.\)
\(\widehat B = 50^\circ .\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 2,5,\,\,\widehat B = 60^\circ .\) Cạnh \(AC\) có độ dài gần nhất với kết quả nào dưới đây?
\(4,33\).
\({\rm{3,4}}{\rm{.}}\)
\({\rm{1,44}}{\rm{.}}\)
\(1,3.\)
