11 câu hỏi
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\[\frac{5}{x} + 8y = 1\].
\[5xy + 8y = 0\].
\(5x - 8y = 0.\)
\[5\frac{x}{y}--\frac{1}{8}y = 0.\]
Phương trình \[4x - 3y = 2\] nhận cặp số nào sau đây làm nghiệm?
\[\left( {1\,;\,\, - 2} \right)\].
\[\left( {1\,;\,\, - 1} \right)\].
\[\left( {2\,;\,\,2} \right)\].
\(\left( {1\,;\,\,1} \right).\)
Trên mặt phẳng tọa độ \[Oxy,\] cho các điểm \[A\left( { - 1\,;\,\, - 1} \right),{\rm{ }}B\left( {2;3} \right),{\rm{ }}C\left( {5;6\,} \right),{\rm{ }}D\left( {1\,;\,\,2} \right).\] Đường thẳng \[ - 4x + 3y = 1\] đi qua hai điểm nào trong các điểm đã cho?
\[A\] và \[B\].
\[B\] và \[C\].
\[C\] và \[D\].
\[D\] và \[A\].
Cặp số nào sau đây là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}5x + 4y = 1\\3x - 2y = 5\end{array} \right.\]?
\[\left( { - 3\,;\,\,2} \right)\].
\[\left( {1\,;\,\, - 1} \right)\].
\[\left( {3\,;\,\, - 2} \right)\].
\[\left( { - 3\,;\,\, - 2} \right).\]
Điều kiện xác định của phương trình \(\frac{1}{{x + 2}} + 1 = \frac{2}{{x - 1}}\) là
\[x \ne - 2;{\rm{ }}x \ne 1\].
\[x \ne 2;{\rm{ }}x \ne 1\].
\[x \ne - 3;{\rm{ }}x \ne --2\].
\[x \ne 1;{\rm{ }}x \ne - 3\].
Cho \(a + 3 > b + 3\), khi đó ta có:
\(a < b.\)
\( - 3a - 3 > - 3b - 3.\)
\(4a < 4b.\)
\(3a + 1 > 3b.\)
Với ba số \(a,b\) và \(c < 0\), các khẳng định sau khẳng định nào đúng?
Nếu \[a > b\] thì \(ac > bc.\)
Nếu \(a > b\) thì \(\frac{a}{c} > \frac{b}{c}.\)
Nếu \(a > b\) thì \(ac < bc.\)
Nếu \(a > b\) thì \(a + c < b + c.\)
Vế trái của bất phương trình \[ - 15x + 4 \le 0\] là
\[ - 15x + 4\].
\[ - 15x\].
\[ - 15x - 4\].
0.
Cho \(\Delta ABC\) vuông tại \[A,\] có \[AB = 3{\rm{ cm}},{\rm{ }}AC = 4{\rm{ cm}},{\rm{ }}BC = 5{\rm{ cm}}.\] Khi đó \(\sin C\) bằng
\(\frac{3}{5}\).
\(\frac{4}{5}\).
\(\frac{5}{4}\).
\(\frac{5}{3}\).
Tính chiều cao \(AH\) với các số liệu cho trên hình sau. Kết quả nào sau đây là đúng?
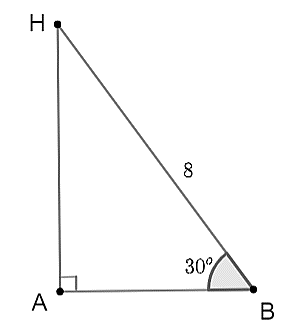
\(AH = 4.\)
\(AH = 2.\)
\(AH = 8.\)
\(AH = 3.\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 10\,\,{\rm{cm}},\,\,\widehat C = 40^\circ .\) Cạnh \(BC\) có độ dài gần nhất với kết quả nào dưới đây?
\(12,45\)cm.
\(15,56\,\,{\rm{cm}}{\rm{.}}\)
\(6,43\,\,{\rm{cm}}{\rm{.}}\)
\(8\)cm.
Gợi ý cho bạn
Xem tất cảĐề thi giữa kì 1 môn Toán lớp 9 Kết nối tri thức có đáp án (Đề 8)
Đề thi giữa kì 1 môn Toán lớp 9 Kết nối tri thức có đáp án (Đề 6)
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 09
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 08