12 câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
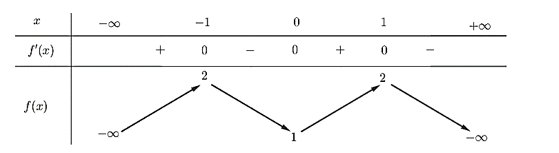
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( {1; + \infty } \right)\).
\(\left( { - 1;0} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\).
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là
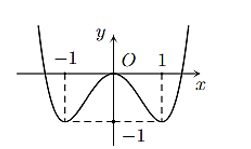
\(\mathop {\min }\limits_D y = - 1\).
\(\mathop {\min }\limits_D y = 1\).
\(\mathop {\min }\limits_D y = 0\).
\(\mathop {\min }\limits_D y = - 2.\)
Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) có bảng biến thiên như sau:
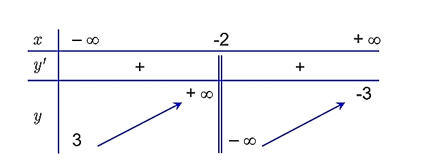
Đồ thị hàm số có bao nhiêu đường tiệm cận
2.
3.
4.
1.
Đồ thị như hình vẽ là của hàm số
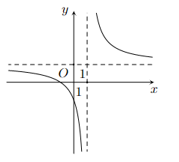
\(y = \frac{{x - 1}}{{ - x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{ - x + 1}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
Hàm số \(y = {x^4} - 2{x^2} + 1\) nghịch biến trên các khoảng nào sau đây?
\(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
\(\left( { - \infty ; - 1} \right)\) và \(\left( {0; + \infty } \right)\).
\(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right)\).
\(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nào sau đây có một đường tiệm cận?
\(y = \frac{{x + 3}}{{2x - 1}}\).
\(y = \frac{{{x^2} + 3x - 2}}{{x + 3}}\).
\(y = \frac{{2x}}{{{x^2} + 1}}\).
\(y = \frac{4}{{x - 1}}\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Khi đó, vectơ bằng vectơ \(\overrightarrow {AB} \) là vectơ nào dưới đây?
\(\overrightarrow {D'C'} \).
\(\overrightarrow {BA} \).
\(\overrightarrow {CD} \).
\(\overrightarrow {B'A'} \).
Trong không gian \(Oxyz\), cho điểm \(M\left( {1; - 2;3} \right)\). Chọn khẳng định đúng trong các khẳng định sau.
\(\overrightarrow {OM} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \).
\(\overrightarrow {MO} = \overrightarrow i - 2\overrightarrow j + 3\overrightarrow k \).
\(\overrightarrow {OM} = \overrightarrow k - 2\overrightarrow j + 3\overrightarrow i \).
\(\overrightarrow {OM} = \overrightarrow j - 2\overrightarrow i + 3\overrightarrow k \).
Gọi \(G\) là trọng tâm của tứ diện \(ABCD\). Trong các khẳng định sau, khẳng định nào sai?
\(\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
\(\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\).
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow u = \left( {1;0; - 1} \right)\) và \(\overrightarrow v = \left( {2;1; - 2} \right)\). Tích vô hướng \(\overrightarrow u .\overrightarrow v \) bằng
0.
1.
4.
2.
Cho mẫu số liệu ghép nhóm cho bởi bảng như hình sau

Khoảng biến thiên của mẫu số liệu là
3.
9.
8.
15.
Cho mẫu số liệu ghép nhóm sau

Gọi \(\overline x \) là số trung bình cộng của mẫu số liệu trên.
\({s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_m}{{\left( {{x_m} - \overline x } \right)}^2}}}{n}\).
Công thức trên dùng để tính
Phương sai.
Độ lệch chuẩn.
Giá trị trung bình.
Độ phân tá
