Đề ôn luyện Toán Chương 8. Một số yếu tố thống kê, xác suất và lý thuyết đồ thị (đề số 3)
22 câu hỏi
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu | \(\left[ {5;7} \right)\) | \(\left[ {7;9} \right)\) | \(\left[ {9;11} \right)\) | \(\left[ {11;13} \right)\) | \(\left[ {13;15} \right)\) |
Số ngày | 2 | 7 | 7 | 3 | 1 |
Khoảng biến thiên của mẫu số liệu trên là giá trị nào trong các giá trị sau?
10.
6.
7.
15.
Kết quả thống kê chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12A ở bảng sau:
Chiều cao (cm) | \(\left[ {155;160} \right)\) | \(\left[ {160;165} \right)\) | \(\left[ {165;170} \right)\) | \(\left[ {170;175} \right)\) | \(\left[ {175;180} \right)\) |
Số học sinh | 5 | 9 | 8 | 2 | 1 |
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm về chiều cao của học sinh nữ lớp 12A (làm tròn đến chữ số thập phân thứ 2) bằng:
160,69.
168,59.
166,24.
167,97.
Khảo sát thời gian sử dụng điện thoại một ngày của học sinh lớp 12A thu được mẫu số liệu ghép nhóm sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên thuộc khoảng nào dưới đây?
\(\left( {22;\,24} \right)\).
\(\left( {20;\,22} \right)\).
\(\left( {18;\,20} \right)\).
\(\left( {24;\,26} \right)\).
Theo thống kê điểm trung bình môn Toán của một số học sinh đã trúng tuyển vào lớp 10 năm học 2024 – 2025 của một trường THPT được kết quả như bảng sau:
Khoảng điểm | \(\left[ {6,5;7} \right)\) | \(\left[ {7;7,5} \right)\) | \(\left[ {7,5;8} \right)\) | \(\left[ {8;8,5} \right)\) | \(\left[ {8,5;9} \right)\) | \(\left[ {9;9,5} \right)\) | \(\left[ {9,5;10} \right)\) |
Tần số | 7 | 10 | 17 | 24 | 13 | 8 | 5 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
\({\rm{\Delta }}Q = 1,1\).
\({\rm{\Delta }}Q = \frac{{228}}{{221}}\).
\({\rm{\Delta }}Q = 1,2\).
\({\rm{\Delta }}Q = \frac{{282}}{{221}}\).
Cho mẫu số liệu ghép nhóm có bảng tần số như sau:
Nhóm | \(\left[ {16;21} \right)\) | \(\left[ {21;26} \right)\) | \(\left[ {26;31} \right)\) | \(\left[ {31;36} \right)\) | \(\left[ {36;41} \right)\) |
Tần số | 4 | 6 | 8 | 18 | 4 |
Tính số trung bình của mẫu số liệu trên.
31.
\(32\).
\(30\).
29.
Khảo sát thời gian tập thể dục của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) | \(\left[ {0;20} \right)\) | \(\left[ {20;40} \right)\) | \(\left[ {40;60} \right)\) | \(\left[ {60;80} \right)\) | \(\left[ {80;100} \right)\) |
Số học sinh | 5 | 9 | 12 | 10 | 6 |
Nhóm chứa trung vị của mẫu số liệu trên là
\(\left[ {20;40} \right)\).
\(\left[ {40;60} \right)\).
\(\left[ {60;80} \right)\).
\(\left[ {80;100} \right)\).
Một tổ học sinh gồm có \(5\) học sinh nữ và \(7\)học sinh nam, chọn ngẫu nhiên \(2\) học sinh. Tính xác suất để \(2\) học sinh được chọn có cả học sinh nam và học sinh nữ.
\[\frac{1}{2}\].
\(\frac{1}{6}\).
\[\frac{{35}}{{66}}\].
\(\frac{3}{{55}}\).
Mỗi bạn Hưng và Nga chọn ngẫu nhiên ba số trong tập \(\left\{ {0;1;2;3;4;5;6;7;8;9} \right\}.\) Xác suất để trong hai bộ số của Hưng và Nga chọn ra có đúng một số giống nhau bằng
\(\frac{{21}}{{40}}.\)
\(\frac{{203}}{{480}}.\)
\(\frac{{49}}{{60}}.\)
\(\frac{{17}}{{24}}.\)
Khảo sát thời gian chạy bộ trong một ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) | \(\left[ {0;20} \right)\) | \(\left[ {20;40} \right)\) | \(\left[ {40;60} \right)\) | \(\left[ {60;80} \right)\) | \(\left[ {80;100} \right)\) |
Số học sinh | \[7\] | \[11\] | \[15\] | \[6\] | \[3\] |
Nhóm chứa mốt của mẫu số liệu này là
\(\left[ {40;60} \right)\).
\(\left[ {60;80} \right)\).
\(\left[ {80;100} \right)\).
\(\left[ {20;40} \right)\).
Thống kê điểm trung bình môn Toán của các học sinh lớp 11A được cho ở bảng sau

Phương sai của mẫu số liệu là
6.
8,5.
0,7.
0,15.
Trong tuần lễ bảo vệ môi trường, các học sinh khối 12 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 12 ở bảng sau:
Số vỏ chai nhựa | \(\left[ {10,5;15,5} \right]\) | \(\left[ {15,5;20,5} \right]\) | \(\left[ {20,5;25,5} \right]\) | \(\left[ {25,5;30,5} \right]\) | \(\left[ {30,5;35,5} \right]\) |
Số học sinh | 53 | 82 | 48 | 39 | 18 |
Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?
19,51.
19,59.
20,1
18,3.
Cho hai biến cố độc lập \(A,B\). Biết \(P\left( A \right) = \frac{1}{5},P\left( B \right) = \frac{2}{3}\). Tính \(P\left( {AB} \right)\).
\(\frac{{11}}{{15}}\).
\(\frac{{13}}{{15}}\).
\(\frac{3}{5}\).
\(\frac{2}{{15}}\).
Trong một hộp đựng \[5\] quả cầu chứa phiếu có thưởng và \[10\] quả cầu chứa phiếu không có thưởng (các quả cầu cùng hình dạng, kích thước và khối lượng). Hai bạn Bình, An lần lượt lấy ngẫu nhiên (không hoàn lại) mỗi bạn một quả. Bạn Bình lấy trước, bạn An lấy sau.
a)Xác suất bạn Bình lấy được quả cầu chứa phiếu có thưởng là \[\frac{1}{2}\].
b)Biết bạn Bình đã lấy được quả cầu chứa phiếu có thưởng, xác suất để bạn An lấy được quả cầu chứa phiếu có thưởng là \[\frac{2}{7}\].
c)Xác suất để hai bạn cùng lấy được quả cầu chứa phiếu có thưởng là \[\frac{2}{{21}}\].
d)Biết An lấy được quả cầu có phiếu có thưởng, xác suất để Bình lấy được quả cầu có phiếu có thưởng là \[\frac{2}{7}\].
Một nhà mạng viễn thông đang triển khai hệ thống phát hiện và chặn các số điện thoại thực hiện cuộc gọi lừa đảo. Tuy nhiên, do hệ thống chưa hoàn hảo, nó có thể chặn nhầm một số điện thoại hợp lệ hoặc bỏ sót một số điện thoại lừa đảo. Hệ thống hoạt động với các thông số sau:
+ Tỷ lệ số điện thoại lừa đảo trong hệ thống: \(5\% \) (tức là \(5\% \) tổng số thuê bao là số lừa đảo).
+ Xác suất hệ thống phát hiện đúng và chặn một số điện thoại lừa đảo: \(94\% \).
+ Xác suất hệ thống chặn nhầm một số điện thoại hợp lệ (tức là số điện thoại không lừa đảo): \(3\% \).
Chọn ngẫu nhiên một số điện thoại đã được thử nghiệm hệ thống.
a) Biết rằng số điện thoại đó là số lừa đảo, xác suất để số điện thoại đó bị chặn là 0,94.
b) Xác suất để một số điện thoại bất kỳ bị chặn là \(\frac{{151}}{{2000}}\).
c) Biết rằng một số điện thoại bị chặn, xác suất để số điện thoại đó là số lừa đảo bằng \(\frac{{90}}{{151}}\).
d) Biết rằng một số điện thoại không bị chặn, xác suất để số điện thoại đó là số hợp lệ bằng \(\frac{{1813}}{{1849}}\).
Một xạ thủ bắn bia, trên bia có các vòng tròn tính điểm (từ 5 đến 10) như hình vẽ.
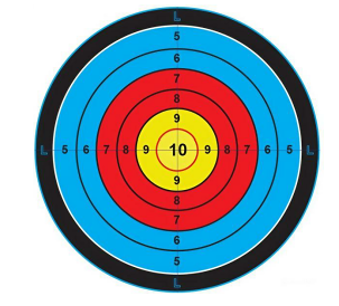
Mỗi lần bắn, xác suất xạ thủ đó bắn trúng vòng 8 là \(0,25\); trúng vòng dưới 8 (kẻ cả bắn trượt) là \(0,4\). Gọi \({P_1},{P_2}\) lần lượt là xác suất xạ thủ đó bắn trúng vòng 10 và vòng 9 trong mỗi lần bắn. Biết rằng nếu xạ thủ đó bắn ba phát vào bia thì xác suất cả ba lần bắn trúng vòng 10 là \(0,003375\).
a)\({P_1} = 0,15\).
b)\({P_2} = 0,18\).
c) Nếu xạ thủ đó bắn ba phát thì xác suất đạt 29 điểm là \(0,0045\).
d) Nếu xạ thủ đó bắn ba phát thì xác suất đạt ít nhất 28 điểm là \(0,05175\).
Trong một giờ ôn tập môn Toán, thầy giáo có chuẩn bị các phiếu học tập gồm hai chủ đề là Thống kê và Xác suất để giao cho 40 bạn học sinh của lớp 12T. Sau khi hết giờ học, thầy giáo thu phiếu và nhận thấy rằng: Có 35 học sinh làm tốt chủ đề Thống kê, có 30 học sinh làm tốt chủ đề Xác suất, có 4 học sinh làm hai chủ đề đều không tốt. Chọn ngẫu nhiên 1 học sinh trong lớp. Gọi các biến cố:
\(A\): “Học sinh được chọn làm tốt chủ đề Thống kê”;
\(B\): “Học sinh được chọn làm tốt chủ đề Xác suất”.
a) \[P\left( A \right) = 0,875\].
b) \(P\left( B \right) = 0,75\).
c) \(P\left( {A \cup B} \right) = 0,8125\).
d) \(P\left( {AB} \right) = 0,725\).
Trên mỗi cạnh của hình bên dưới, có ghi số phút để đi từ điểm này đến điểm kế tiếp.
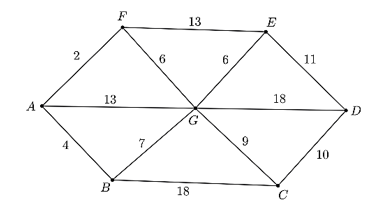
Tìm tổng thời gian ngắn nhất để di chuyển từ điểm A đến điểm D trên hình.
Một cơ quan hành chính nhà nước thực hiện việc tinh giản biên chế thông qua phỏng vấn. Tỷ lệ nhân viên của cơ quan này thuộc hai nhóm trình độ: đại học, cao đẳng lần lượt là \[65\% \] và \[35\% \]. Qua phỏng vấn thì tỷ lệ nhân viên bị tinh giản của nhóm đại học là \[10\% \], nhóm cao đẳng là \[15\% \]. Chọn một nhân viên bất kỳ đã bị tinh giản thì hãy tính xác suất để người này có trình độ đại học (kết quả là một số thập phân nhỏ hơn 1 đã làm tròn đến hàng phần trăm).
Công ty X có một kho hàng trung tâm tại điểm A và cần giao hàng đến 3 điểm giao hàng khác nhau B, C, D trong thành phố, sau khi giao hàng xong thì xe quay về điểm A. Biết rằng khoảng cách giữa các điểm giao hàng cho bởi bảng sau (đơn vị tính km).
Điểm đến Điểm đi | A | B | C | D |
A | 0 | 9 | 11 | 14 |
B | 9 | 0 | 7 | 8 |
C | 11 | 7 | 0 | 5 |
D | 14 | 8 | 5 | 0 |
Thời gian giao hàng tại mỗi điểm giao hàng 30 phút/điểm. Tốc độ trung bình của xe vận chuyển hàng là 40km/h. Tính tổng thời gian ít nhất để hoàn thành việc giao hàng nói trên (đơn vị đo: phút, làm tròn đến hàng đơn vị).
Một nhà đầu tư đang xem xét đầu tư vào hai loại tài sản: Cổ phiếu và trái phiếu. Qua nghiên cứu thị trường có hai kịch bản sau có thể xảy ra:
- Kịch bản kinh tế tăng trưởng: Xác suất xảy ra kịch bản kinh tế tăng trưởng trong năm tới là \[60\% \]. Trong kịch bản này, xác suất cổ phiếu mang lại lợi nhuận cao là \[80\% \] và xác suất trái phiếu mang lại lợi nhuận cao là \[30\% \].
- Kịch bản kinh tế suy thoái: Xác suất xảy ra kịch bản kinh tế suy thoái trong năm tới là \[40\% \]. Trong kịch bản này, xác suất cổ phiếu mang lại lợi nhuận cao là \[10\% \] và xác suất trái phiếu mang lại lợi nhuận cao là \[70\% \].
Vào cuối năm, nhà đầu tư nhận thấy rằng trái phiếu đã mang lại lợi nhuận cao. Tính xác suất để kịch bản kinh tế trong năm đó là suy thoái (làm tròn kết quả đến hàng phần trăm).
Trong cuộc gặp mặt dặn dò trước khi lên đường tham gia kì thi học sinh giỏi, có 10 bạn trong đội tuyển gồm 2 bạn đến từ lớp 12A, 3 bạn đến từ lớp 12B, 5 bạn còn lại đến từ 5 lớp khác (mỗi lớp 1 bạn). Thầy giáo xếp ngẫu nhiên các bạn kể trên vào một bàn dài có 10 ghế mà mỗi bên có 5 ghế đối diện nhau. Tính xác suất để không có học sinh nào cùng lớp ngồi đối diện nhau (làm tròn kết quả đến hàng phần chục).
Thống kê thời gian tự học môn Toán của 400 học sinh lớp 12 trong một ngày ta được kết quả trong bảng ghép nhóm sau:

Biết rằng \(x,y\) là các số nguyên dương và khoảng tứ phân vị của mẫu số liệu bằng \(\frac{{845}}{{21}}\). Khi đó, thời gian tự học trung bình của 400 học sinh (tính theo mẫu số liệu ghép nhóm trên) là bao nhiêu phút?