Đề ôn luyện Toán Chương 8. Một số yếu tố thống kê, xác suất và lý thuyết đồ thị (đề số 2)
22 câu hỏi
Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng 3 thì có phương sai bằng:
\({s^2} = 3\).
\({s^2} = 6\).
\({s^2} = 9\).
\({s^2} = \sqrt 3 \).
Cho bảng thống kê doanh số bán hàng của 100 nhân viên ở một trung tâm thương mại trong một tuần như sau:
Doanh số (triệu đồng) | \(\left[ {20\,;\,30} \right)\) | \(\left[ {30\,;\,40} \right)\) | \(\left[ {40\,;\,50} \right)\) | \(\left[ {50\,;\,60} \right)\) | \(\left[ {60\,;\,70} \right)\) | \(\left[ {70\,;\,80} \right)\) |
Số nhân viên | 25 | 20 | 20 | 15 | 14 | 6 |
Trung tâm thương mại dự định chọn 25% số nhân viên có doanh số bán hàng cao nhất để trao thưởng. Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán hàng ít nhất là bao nhiêu triệu đồng (kết quả làm tròn đến hàng phần chục)?
30,0 triệu đồng.
42,5 triệu đồng.
56,7 triệu đồng.
53,7 triệu đồng.
Khảo sát trọng lượng của một số quả mít được trồng trong một nông trường ta có mẫu số liệu sau:
Cân nặng (kg) | \(\left[ {4;6} \right)\) | \(\left[ {6;8} \right)\) | \(\left[ {8;10} \right)\) | \(\left[ {10;12} \right)\) | \(\left[ {12;14} \right)\) |
Số quả mít | 6 | 12 | 19 | 9 | 4 |
Tìm độ lệch tiêu chuẩn của mẫu số liệu trên (kết quả làm tròn đến hàng phần trăm).
\(2,19\).
\(8,72\).
\(4,80\).
\(2,20\).
Thời gian (đơn vị: phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Thời gian (phút) | \(\left[ {9,5;12,5} \right)\) | \(\left[ {12,5;15,5} \right)\) | \(\left[ {15,5;18,5} \right)\) | \(\left[ {18,5;21,5} \right)\) | \(\left[ {21,5;24,5} \right)\) |
Số học sinh | 3 | 12 | 15 | 24 | 2 |
Khoảng tứ phân vị của mẫu số liệu trên là
10,75.
4,75.
4,63.
4,38
Bảng thống kê dưới đây cho biết thu nhập bình quân đầu người/tháng của người dân Hà Nội (tính theo triệu đồng) trong giai đoạn từ năm 2018 đến năm 2024:
Năm | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 |
Thu nhập (triệu đồng/ tháng) | 5,901 | 6,403 | 6,203 | 6,002 | 6,423 | 6,869 | 7,546 |
Mẫu số liệu thống kê trên có khoảng biến thiên bằng bao nhiêu (tính theo triệu đồng)?
2,660.
1,645.
0,867.
2,290
Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một nhóm học sinh thu được kết quả sau:
Thời gian (phút) | \(\left[ {0;4} \right)\) | \(\left[ {4;8} \right)\) | \(\left[ {8;12} \right)\) | \(\left[ {12;16} \right)\) | \(\left[ {16;20} \right)\) |
Số học sinh | \(2\) | \(4\) | \(7\) | \(4\) | \(3\) |
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
\(10,4\).
\(7\).
\(11,3\).
\(12,5\).
Bảng số liệu ghép nhóm về chiều cao đo được (đơn vị: cm) của 30 học sinh nam lớp 12A2 đầu năm học 2024 – 2025 của một trường THPT được cho như sau:
Chiều cao | \(\left[ {150;155} \right)\) | \(\left[ {155;160} \right)\) | \(\left[ {160;165} \right)\) | \(\left[ {165;170} \right)\) | \(\left[ {170;175} \right)\) |
Tần số | 3 | 7 | 10 | 7 | 3 |
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là
\(\frac{{\sqrt {285} }}{3}\).
\(\frac{{\sqrt {287} }}{3}\).
\(4\sqrt 2 \).
\(\sqrt {71} \).
Khảo sát thời gian tập thể dục của họ sinh khối 12 tại một trường THPT thu được mẫu số liệu ghép nhóm sau đây
Thời gian (phút) | \[\left[ {0;20} \right)\] | \[\left[ {20;40} \right)\] | \[\left[ {40;60} \right)\] | \[\left[ {60;80} \right)\] | \[\left[ {80;100} \right)\] |
Số học sinh | 5 | 9 | 12 | 10 | 6 |
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là
\[\left[ {40;60} \right)\].
\[\left[ {60;80} \right)\].
\[\left[ {20;40} \right)\].
\[\left[ {80;100} \right)\].
Bạn Trí rất thích nhảy dân vũ. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Trí được thống kê lại ở bảng sau:
Thời gian (phút) | \(\left[ {20;\,25} \right)\) | \(\left[ {25;\,30} \right)\) | \(\left[ {30;\,35} \right)\) | \(\left[ {35;\,40} \right)\) | \(\left[ {40;\;45} \right)\) |
Số ngày | 6 | 6 | 4 | 1 | 1 |
Phương sai của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là
31,77.
31,25.
31,44.
32,25
An và Bình không quen biết nhau và học ở hai nơi khác nhau. Xác suất để An và Bình đạt điểm giỏi về môn Toán trong kì thi cuối năm tương ứng là \[0,92\] và \[0,88\]. Tính xác suất để cả An và Bình đều không đạt điểm giỏi.
\[0,0096\].
\[0,3597\].
\[0,8096\].
\[0,3649\].
Cho mẫu số liệu điểm môn Toán của một nhóm học sinh như sau:
Điểm | \(\left[ {6 ; 7} \right)\) | \(\left[ {7 ; 8} \right)\) | \(\left[ {8 ; 9} \right)\) | \(\left[ {9 ; 10} \right]\) |
Số học sinh | \(8\) | \(7\) | \(10\) | \(5\) |
Mốt của mẫu số liệu trên (kết quả làm tròn đến hàng phần trăm) là:
\(7,91\).
\(8,38\).
\(8,37\).
\(7,95\).
Từ một hộp chứa \(11\) quả cầu màu đỏ và \(4\) quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được \(3\) quả cầu màu xanh là
\(\frac{{33}}{{91}}\).
\(\frac{4}{{455}}\).
\(\frac{4}{{165}}\).
\(\frac{{24}}{{455}}\).
Một nhà máy có hai phân xưởng \(A\) và \(B\) tương ứng làm ra \(60\% \)và \(40\% \) sản phẩm của nhà máy. Tỉ lệ phế phẩm của hai phân xưởng \(A\) và \(B\)lần lượt là \(1\% \)và \(2\% \). Chọn ngẫu nhiên một sản phẩm của nhà máy.
a) Nếu sản phẩm chọn ra thuộc phân xưởng \(A\) thì xác suất để nó không là phế phẩm là \(0,98\).
b) Xác suất để sản phẩm chọn ra là phế phẩm và thuộc phân xưởng \(A\) là \(0,006\).
c) Xác suất để sản phẩm chọn ra là phế phẩm là \(0,014\).
d) Nếu sản phẩm chọn ra là phế phẩm thì xác suất để nó thuộc phân xưởng \(A\) là \(\frac{4}{7}\).
Các thí sinh tham dự một cuộc thi hoa khôi phải trải qua ba vòng thi: vòng sơ khảo, vòng bán kết và vòng chung kết. Biết rằng, ban tổ chức sẽ chọn ra \(50{\rm{\% }}\) thí sinh đã đăng kí để vào vòng sơ khảo. Khi kết thúc vòng sơ khảo, ban tổ chức sẽ chọn ra \(30{\rm{\% }}\) thí sinh của vòng sơ khảo để vào vòng bán kết. Khi kết thúc vòng bán kết, ban tổ chức sẽ chọn ra \(20{\rm{\% }}\) thí sinh của vòng bán kết để vào vòng chung kết. Chọn ngẫu nhiên 1 thí sinh đăng kí tham dự cuộc thi hoa khôi.
a) Xác suất để thí sinh được chọn lọt vào vòng sơ khảo là \(0,5\).
b) Xác suất để thí sinh được chọn lọt vào vòng bán kết là \(0,3\).
c) Xác suất thí sinh được chọn lọt vào vòng chung kết là \(0,03\).
d) Biết rằng thí sinh được chọn không lọt vào vòng chung kết, xác suất thí sinh đó lọt vào vòng sơ khảo nhỏ hơn \(0,49\).
Có hai phác đồ điều trị \(A\) và \(B\) cho một loại bệnh. Phác đồ \(A\) có xác suất chữa khỏi bệnh là \(60\% \) và xác suất gây tác dụng phụ nghiêm trọng là \(5\% .\) Phác đồ \(B\) có xác suất chữa khỏi bệnh là \(70\% \) và xác suất gây tác dụng phụ nghiêm trọng là \(10\% .\) Một bệnh nhân được điều trị ngẫu nhiên bằng một trong hai phác đồ (xác suất chọn mỗi phác đồ là \(50\% \)).
a) Xác suất bệnh nhân điều trị bằng phác đồ \(A\) và được chữa khỏi bệnh là \(0,6.\)
b) Xác suất để bệnh nhân bị tác dụng phụ nghiêm trọng là \(0,075.\)
c) Nếu biết bệnh nhân này gặp tác dụng phụ nghiêm trọng thì xác suất bệnh nhân đã được điều trị bằng phác đồ \(B\) lớn hơn \(0,65.\)
d) Biết rằng trong mỗi phác đồ điều trị thì biến cố “bệnh nhân được chữa khỏi bệnh” và biến cố “bệnh nhân không bị tác dụng phụ nghiêm trọng” là độc lập với nhau. Xác suất bệnh nhân khỏi bệnh và không bị tác dụng phụ nghiêm trọng là \(0,6\).
Một hộp có chứa \(5\)viên bi đỏ, \(3\)viên bi xanh và \(n\) viên bi vàng (các viên bi kích thước như nhau, \(n\) là số nguyên dương). Lấy ngẫu nhiên \(3\) viên bi từ hộp. Biết xác suất để trong ba viên bi lấy được có đủ \(3\) màu là \(\frac{{45}}{{182}}\).
a) Số cách lấy \(3\) viên bi có đủ \(3\) màu là \(C_5^1 + C_3^1 + C_n^1\).
b) Số bi vàng là \(n = 8\).
c) Xác suất để \(3\) bi lấy ra chỉ có \(1\) màu là \(\frac{{31}}{{364}}\).
d) Xác suất để trong \(3\) viên bi lấy được có nhiều nhất hai viên bi đỏ là \(\frac{{135}}{{364}}\).
Người ta ghi chép lại trọng lượng (gam) một loại cá rô được nuôi trong ao theo một chế độ đặc biệt sau 6 tháng, họ có bảng tần số ghép nhóm sau:
Trọng lượng | \(\left[ {60;70} \right)\) | \(\left[ {70;80} \right)\) | \(\left[ {80;90} \right)\) | \(\left[ {90;100} \right)\) | \(\left[ {100;110} \right)\) | \(\left[ {110;120} \right)\) |
Số cá | 13 | 24 | 55 | 61 | 31 | 16 |
Tìm trung vị của mẫu số liệu (làm tròn kết quả đến hàng phần chục)
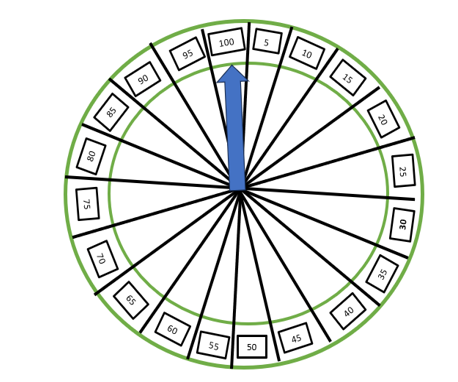
Hai bạn Hùng và Cường chơi trò quay bánh xe số. Bánh xe số có \(20\) nấc điểm là \(5,10,15,.....,100\)với các vạch chia đều nhau (giả sử rằng khả năng chuyển từ nấc điểm đã có tới các nấc điểm còn lại là như nhau). Trong mỗi lượt chơi, mỗi người được quyền chọn quay \(1\) hoặc \(2\)lần và điểm số của người chơi được tính như sau:
(1) Nếu người chơi chọn quay một lần thì điểm của người chơi là điểm quay được.
(2) Nếu người chơi chọn quay \(2\) lần và tổng điểm quay được không lớn hơn \(100\) thì điểm của người chơi là tổng điểm quay được.
(3) Nếu người chơi chọn quay \(2\) lần và tổng điểm quay được lớn hơn \(100\)thì điểm người chơi là tổng điểm quay được trừ đi \(100\).
Luật chơi quy định, trong mỗi lượt chơi người nào có điểm số cao hơn sẽ thắng cuộc, hòa nhau sẽ chơi lại lượt khác. Hùng chơi trước và có điểm số là \(75\). Tính xác suất để Cường thắng cuộc ngay ở lượt chơi này (lấy kết quả đến hàng phần trăm).
Một chiếc hộp có 50 viên bi, trong đó có 30 viên bi màu xanh và 20 viên bi màu đỏ, các viên bi có kích thước và khối lượng giống nhau. Sau khi kiểm tra, người ta thấy có 70% số viên bi màu xanh được đánh số và 60% số viên bi màu đỏ được đánh số, những viên bi còn lại không đánh số. Lấy ngẫu nhiên một viên bi từ hộp đó. Biết rằng, viên bi lấy ra được đánh số, xác suất để viên bi đó có màu xanh bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Trong chuyện cổ tích “Cây tre trăm đốt”, khi không vác được cây tre dài đến \[100\] đốt về nhà, anh Khoai ngồi khóc. Bụt hiện lên, bày cho anh một cách hay: “Con hãy đọc câu thần chú “khắc xuất, khắc xuất” thì cây tre sẽ phân tách ra nhiều thanh nhỏ để con có thể mang được về nhà. Biết rằng sau mỗi câu thần chú như thế thì cây tre \[100\] đốt được tách ra một cách ngẫu nhiên thành các đoạn ngắn có chiều dài \[2\] đốt và \[5\] đốt (có thể chỉ có một loại). Tính xác suất để số đoạn \[2\] đốt nhiều hơn số đoạn \[5\] đốt đúng \[1\] đơn vị (làm tròn kết quả đến hàng phần trăm).
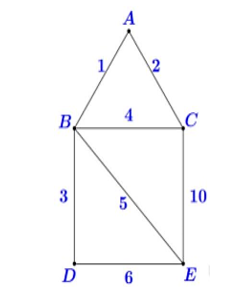
Một người đưa thư xuất phát từ bưu điện (vị trí C), các điểm cần phát thư nằm dọc các con đường cần đi qua. Biết rằng người này phải đi trên mỗi con đường ít nhất một tần (để phát được thư cho tất cả các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Sơ đồ các con đường cần đi qua và độ dài của chúng (tính theo kilomet) được biểu diễn ở hình vẽ. Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể là bao nhiêu kilomet?
Một đoàn tình nguyện đến một trường tiểu học miền núi để trao tặng 20 suất quà cho 10 em học sinh nghèo học giỏi. Trong 20 suất quà đó gồm 7 chiếc áo mùa đông, 9 thùng sữa tươi và 4 chiếc cặp sách. Tất cả các suất quà đều có giá trị tương đương nhau. Biết rằng mỗi em nhận 2 suất quà khác loại (ví dụ một chiếc áo và một thùng sữa tươi). Trong số các em nhận quà có hai em Hà và Vương. Tính xác suất để hai em đó nhận được suất quà giống nhau.