Đề ôn luyện Toán Chương 8. Một số yếu tố thống kê, xác suất và lý thuyết đồ thị (đề số 1)
22 câu hỏi
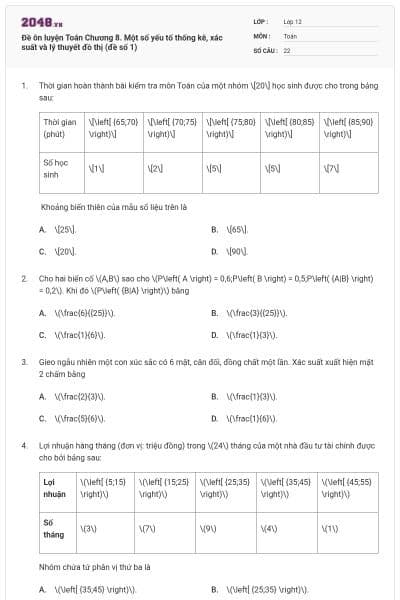
Thời gian hoàn thành bài kiểm tra môn Toán của một nhóm \[20\] học sinh được cho trong bảng sau:
Thời gian (phút) | \[\left[ {65;70} \right)\] | \[\left[ {70;75} \right)\] | \[\left[ {75;80} \right)\] | \[\left[ {80;85} \right)\] | \[\left[ {85;90} \right)\] |
Số học sinh | \[1\] | \[2\] | \[5\] | \[5\] | \[7\] |
Khoảng biến thiên của mẫu số liệu trên là
\[25\].
\[65\].
\[20\].
\[90\].
Cho hai biến cố \(A,B\) sao cho \(P\left( A \right) = 0,6;P\left( B \right) = 0,5;P\left( {A|B} \right) = 0,2\). Khi đó \(P\left( {B|A} \right)\) bằng
\(\frac{6}{{25}}\).
\(\frac{3}{{25}}\).
\(\frac{1}{6}\).
\(\frac{1}{3}\).
Gieo ngẫu nhiên một con xúc sắc có 6 mặt, cân đối, đồng chất một lần. Xác suất xuất hiện mặt 2 chấm bằng
\(\frac{2}{3}\).
\(\frac{1}{3}\).
\(\frac{5}{6}\).
\(\frac{1}{6}\).
Lợi nhuận hàng tháng (đơn vị: triệu đồng) trong \(24\) tháng của một nhà đầu tư tài chính được cho bởi bảng sau:
Lợi nhuận | \(\left[ {5;15} \right)\) | \(\left[ {15;25} \right)\) | \(\left[ {25;35} \right)\) | \(\left[ {35;45} \right)\) | \(\left[ {45;55} \right)\) |
Số tháng | \(3\) | \(7\) | \(9\) | \(4\) | \(1\) |
Nhóm chứa tứ phân vị thứ ba là
\(\left[ {35;45} \right)\).
\(\left[ {25;35} \right)\).
\(\left[ {15;25} \right)\).
\(\left[ {45;55} \right)\).
Cho \(A\) và \(B\) là hai biến cố độc lập thoả mãn \(P\left( A \right) = 0,5\) và \(P\left( B \right) = 0,3\). Khi đó, \(P\left( {A \cap B} \right)\) bằng:
0,8.
0,2.
0,6.
0,15.
Một hộp chứa 7 viên bi đỏ, 8 viên bi trắng, 6 viên bi vàng. Lấy ngẫu nhiên trong hộp ra 4 viên bi. Tính xác suất để chọn được 4 viên bi trong đó có nhiều nhất 2 viên bi vàng.
\(\frac{{12}}{{13}}\).
\(\frac{{15}}{{16}}\).
\(\frac{{13}}{{14}}\).
\(\frac{{18}}{{19}}\).
Cho mẫu số liệu ghép nhóm về khoảng tuổi và số người như bảng sau:
Khoảng tuổi | \(\left[ {22\,;\,31} \right)\) | \(\left[ {31\,;\,40} \right)\) | \(\left[ {40\,;\,49} \right)\) | \(\left[ {49\,;\,58} \right)\) | \(\left[ {58\,;\,67} \right)\) | \(\left[ {67\,;\,76} \right)\) |
Số người | \(33\) | \(23\) | \(23\) | \(16\) | \(16\) | \(9\) |
Khoảng tứ phân vị (làm tròn kết quả đến hàng phần trăm) của mẫu số liệu ghép nhóm đã cho bằng
\(13,62.\)
\(25,01.\)
\(11,38.\)
\(32,18.\)
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Mốt của mẫu số liệu trên là
\[52\].
\[42\].
\[53\].
\[54\].
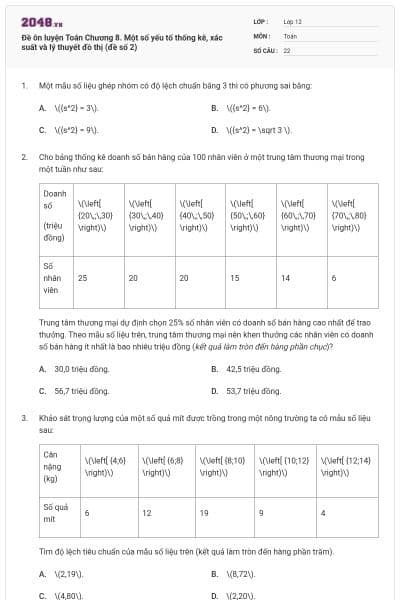
Cho mẫu số liệu ghép nhóm về lương (triệu đồng) và số nhân viên như sau:
Lương (triệu đồng) | \(\left[ {5\,;11} \right)\) | \(\left[ {11\,;17} \right)\) | \(\left[ {17;23} \right)\) | \(\left[ {23;29} \right)\) | \(\left[ {29\,;35} \right)\) |
Số nhân viên | 15 | 14 | 7 | 12 | 10 |
Độ lệch chuẩn (làm tròn kết quả đến hàng phần trăm) của mẫu số liệu ghép nhóm trên bằng
\[8,87\].
\[8,76\].
\[8,74\].
\[2,29\].
Khối lượng các gói kẹo được đóng gói (đơn vị là kg) được thống kê ở bảng sau:
Khối lượng (kg) | \(\left[ {1,5;1,7} \right)\) | \(\left[ {1,7;1,9} \right)\) | \(\left[ {1,9;2,1} \right)\) | \(\left[ {2,1;2,3} \right)\) | \(\left[ {2,3;2,5} \right)\) |
Số gói kẹo | 3 | 5 | 23 | 5 | 4 |
Phương sai của mẫu số liệu ghép nhóm trên gần nhất với kết quả nào sau đây?
0,08.
0,07.
0,09.
0,04.
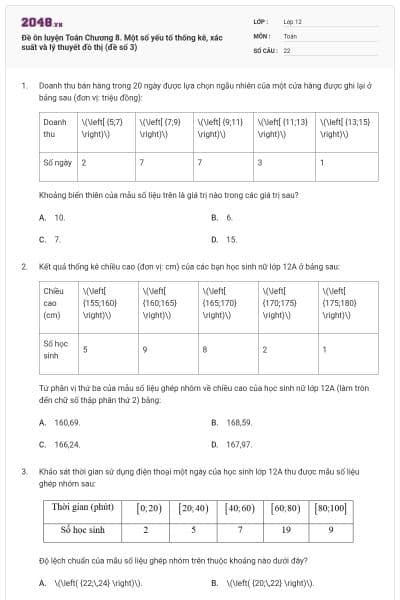
Để chuẩn bị cho tiết học “Mạng xã hội: lợi và hại”, giáo viên đã khảo sát thời gian sử dụng mạng xã hội trong một ngày của học sinh trong lớp 10A1 mình dạy và thu được mẫu số liệu như sau:
Thời gian sử dụng mạng xã hội (phút) | \(\left[ {10;20} \right)\) | \(\left[ {20;30} \right)\) | \(\left[ {30;40} \right)\) | \(\left[ {40;50} \right)\) | \(\left[ {50;60} \right)\) | \(\left[ {60;70} \right)\) |
Số học sinh | 5 | 10 | 15 | 7 | 5 | 3 |
Thời gian trung bình (phút) sử dụng mạng xã hội của học sinh lớp 10A1 xấp xỉ bằng
\(35\).
\(36,3\).
\(33,6\).
\(30,5\,\).
Cho hai biến cố độc lập \(A\) và \(B\). Biết \(P\left( A \right) = \frac{1}{4},P\left( {A \cup B} \right) = \frac{1}{2}\). Tính \(P\left( B \right)\).
\(\frac{3}{4}\).
\(\frac{1}{4}\).
\(\frac{1}{8}\).
\(\frac{1}{3}\).
Có hai hộp chứa các tấm thẻ. Hộp I chứa 8 tấm thẻ màu vàng được đánh số từ 1 đến 8, hộp II chứa 9 tấm thẻ màu đỏ được đánh số từ 1 đến 9. Lấy ngẫu nhiên từ mỗi hộp một tấm thẻ.
a) Số phần tử của không gian mẫu là \(72\).
b) Sau khi 2 tấm thẻ được lấy ra ta ghép hai chữ số trên hai tấm thẻ với nhau để được một số có hai chữ số (chữ số hàng chục là số trên tấm thẻ màu vàng và chữ số hàng đơn vị là số trên tấm thẻ màu đỏ). Xác suất để thu được số chia hết cho 3 bằng \(\frac{3}{{10}}\).
c) Xác suất chọn được hai tấm thẻ có số giống nhau bằng \(\frac{1}{9}\).
d) Xác suất để tích các số trên hai tấm thẻ lấy được là một số chẵn bằng \(\frac{5}{{18}}\).
Một nhà máy có hai phân xưởng cùng sản xuất một loại sản phẩm. Phân xưởng thứ nhất sản xuất \(60{\rm{\% }}\) và phân xưởng thứ hai sản xuất \(40{\rm{\% }}\) tổng số sản phẩm của cả nhà máy. Tỉ lệ phế phẩm của từng phân xưởng lần lượt là \(16{\rm{\% }}\) và \(20{\rm{\% }}\). Lấy ngẫu nhiên một sản phẩm trong kho hàng của nhà máy.
a) Xác suất để sản phẩm đó do phân xưởng thứ nhất sản xuất là 0,6.
b) Xác suất để lấy được phế phẩm bằng 0,176.
c) Giả sử đã lấy được phế phẩm, xác suất phế phẩm đó do phân xưởng thứ nhất sản xuất bằng 0,55 (kết quả làm tròn đến hàng phần trăm).
d) Nếu lấy được sản phẩm tốt, khả năng sản phẩm đó do phân xưởng thứ hai sản xuất là cao hơn khả năng sản phẩm đó do phân xưởng thứ nhất sản xuất.
Khảo sát những người xem bộ phim hoạt hình vừa được phát hành cho thấy \(70\% \) người xem là trẻ em và \(30\% \) là người lớn. Trong số các trẻ em đến xem phim có \(50\% \) yêu thích bộ phim và khẳng định sẽ đi xem tiếp phần 2, \(30\% \) yêu thích bộ phim nhưng sẽ không xem tiếp phần 2; \(20\% \) còn lại không thích bộ phim và không xem tiếp phần 2. Trong số những người lớn đi xem phim có \(20\% \) yêu thích bộ phim và khẳng định sẽ xem tiếp phần 2, \(10\% \) yêu thích bộ phim nhưng sẽ không xem tiếp phần 2; \(70\% \) còn lại không thích bộ phim và không xem tiếp phần 2. Chọn ngẫu nhiên 1 người đã xem phim.
a)Biết người được chọn là trẻ em, xác suất để người đó yêu thích bộ phim là \(0,56\).
b)Xác suất để người đó không xem tiếp phần 2 là \(0,59\).
c)Biết người đó sẽ xem tiếp phần 2 của bộ phim, xác suất để người đó là trẻ em lớn hơn \(0,85\).
d)Biết người đó yêu thích bộ phim, xác suất để người đó không xem tiếp phần 2 là \(0,37\) (làm tròn đến hàng phần trăm).
Kết quả \(40\) lần nhảy xa của hai vận động viên Dũng và Huy được lần lượt thống kê trong bảng bên (đơn vị: mét).
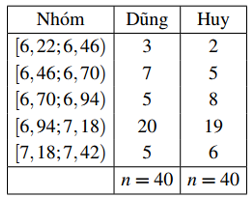
a) Số trung bình cộng của mẫu số liệu ghép nhóm biểu diễn kết quả 40 lần nhảy xa của vận động viên Dũng (làm tròn kết quả đến hàng phần trăm) là \(6,92\)m.
b) Độ lệch chuẩn của mẫu số liệu ghép nhóm biểu diễn kết quả 40 lần nhảy xa của vận động viên Dũng (làm tròn kết quả đến hàng phần trăm) là \(0,26\)m.
c) Phương sai của mẫu số liệu ghép nhóm biểu diễn kết quả 40 lần nhảy xa của vận động viên Huy (làm tròn kết quả đến hàng phần trăm) là \(0,16\).
d) Kết quả nhảy xa của vận động viên Dũng đồng đều hơn kết quả nhảy xa của vận động viên Huy.
Có \[6\]học sinh lớp \[11\] và \[3\]học sinh lớp 12 được xếp ngẫu nhiên thành một hàng ngang. Xác suất để khi xếp ngẫu nhiên \[9\] học sinh đó sao cho không có hai học sinh lớp 12 nào đứng cạnh nhau bằng \[\frac{a}{b}\](trong đó \[\frac{a}{b}\] là phân số tối giản). Khi đó \[2a + b\]bằng bao nhiêu?
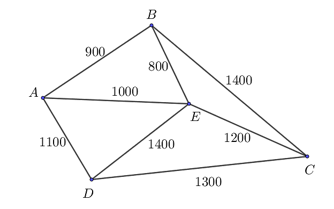
Một công ty vận tải cần giao hàng đến tất cả các thành phố \(A,\;B,\;C,\;D,\;E\) (xem hình vẽ). Chi phí di chuyển giữa các thành phố được mô tả trên hình (tính theo đơn vị nghìn đồng). Xe giao hàng của công ty xuất phát từ thành phố \(A\) đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố \(A\). Tìm chi phí thấp nhất của xe giao hàng (tính theo đơn vị nghìn đồng)?
Một công ty xây dựng đấu thầu ba dự án \(X,\,\,Y\) và \(Z\). Xác suất để ba dự án \(X,\,\,Y\) và \(Z\) trúng thầu tương ứng là \(a;\,\,b\) và \(0,8\,\,\left( {a > b} \right)\). Biết rằng xác suất để ít nhất một trong ba dự án trúng thầu là \(0,964\) và xác suất để cả ba dự án đều trúng thầu là \(0,224\). Giả sử việc trúng thầu của ba dự án \(X,\,\,Y\) và \(Z\) là độc lập với nhau. Tính \[2a + b\].
Trong một giải thi đấu bóng chuyền, đội bóng chuyền của Hà Nội sẽ thi đấu hai trận. Trận thứ nhất đội bóng chuyền của Hà Nội có xác suất thắng là \(0,6\). Trận tiếp theo, xác suất chiến thắng của họ phụ thuộc vào kết quả trận trước đó. Nếu đội bóng chuyền của Hà Nội thắng trận trước đó, họ sẽ hưng phấn và xác suất để họ thắng là \(0,7\). Nếu đội bóng chuyền của Hà Nội thua trận trước thì họ sẽ mất tinh thần và xác suất để họ thắng là \(0,5\). Tính xác suất để đội bóng chuyền của Hà Nội thắng trận thứ hai.
Nhân dịp kỷ niệm \[50\] năm ngày thành lập trường, các học sinh lựa chọn tham gia thi đấu thể thao hoặc biểu diễn văn nghệ. Lớp 12A có \[60\% \] số học sinh tham gia thi đấu thể thao và còn lại \[40\% \] số học sinh tham gia biểu diễn văn nghệ. Biết rằng các bạn nữ đều tham gia biểu diễn văn nghệ. Trong số các bạn nam có \[20\% \] tham gia văn nghệ và \[80\% \] tham gia thi đấu thể thao. Chọn ngẫu nhiên \[1\] học sinh trong lớp. Biết rằng học sinh này tham gia biểu diễn văn nghệ, xác suất để học sinh này là nữ bằng bao nhiêu phần trăm?
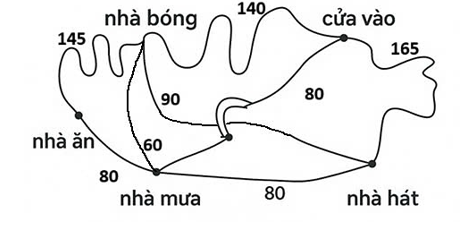
Một công viên thuê sinh viên tuần tra các con đường và thu gom rác. Các con đường phải tuần tra thể hiện trong sơ đồ dưới đây, với các khoảng cách tính bằng mét. Con đường nối từ nhà bóng tới nhà hát đi dưới một cây cầu nằm trên con đường nối từ nhà mưa tới cửa vào. Biết rằng sinh viên xuất phát từ cửa vào, đi qua tất cả các con đường để tuần tra và dọn rác và kết thúc công việc cũng ở cửa vào. Hỏi quãng đường ngắn nhất mà sinh viên đó đi là bao nhiêu mét?