Đề kiểm tra Toán 12 Cánh diều Chương 4 có đáp án - Đề 2
11 câu hỏi
Tìm nguyên hàm của hàm số \(f\left( x \right) = 2025\sin x\).
\(\int {2025\sin x\,{\rm{d}}x} = \sin 2025x + C\).
\(\int {2025\sin x\,{\rm{d}}x} = {\sin ^{2025}}x + C\).
\(\int {2025\sin x\,{\rm{d}}x} = - 2025\cos x + C\).
\(\int {2025\sin x\,{\rm{d}}x} = 2025\cos x + C\).
Cho hàm số\[f\left( x \right) = {e^x} + 2x\]. Khẳng định nào dưới đây đúng?
\[\int {f\left( x \right)} = {e^x} + 2x + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} + 2{x^2} + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} - {x^2} + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} + {x^2} + C\].
Biết \(\int\limits_0^1 {f\left( x \right){\rm{d}}x = 3} \) và \(\int\limits_0^1 {g\left( x \right){\rm{d}}x = - 2} \). Khi đó \[\int\limits_0^1 {\left[ {f\left( x \right) + g\left( x \right)} \right]{\rm{d}}x} \] bằng
\(1.\)
\(5.\)
\( - 1\).
\( - 6.\)
Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là \(x(0 \le x \le 3)\) ta được mặt cắt là một hình vuông có cạnh là \(\sqrt {9 - {x^2}} \) (được mô hình hóa bởi hình vẽ bên dưới).
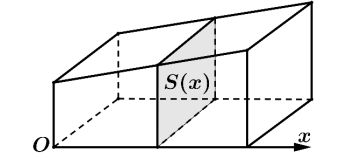
Thể tích của vật thể đó bằng
\(171\pi \).
\(18\pi \).
\(18\).
\(171\)
Hàm số \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right) = 3{x^2}\) và \(F\left( 0 \right) = 5\). Khi đó, hàm số \(F\left( x \right)\) là
\(F\left( x \right) = 3{x^3} + 5\).
\(F\left( x \right) = {x^3} - 5\).
\(F\left( x \right) = {x^3} + 5\).
\(F\left( x \right) = 6x + 5\).
Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = \sin x,\;y = \cos x\) và các đường thẳng \(x = 0,\;x = 7\)được tính bằng công thức
\(S = \int\limits_0^7 {( - \sin x + {\rm{cos}}x){\rm{d}}x} \).
\[S = \int\limits_0^7 {\left| {{\rm{sin}}x - {\rm{cos}}x} \right|} {\rm{d}}x\].
\[S = \int\limits_0^7 {({\rm{sin}}x - {\rm{cos}}x){\rm{d}}x} \].
\[S = \int\limits_0^7 {({\rm{sin}}x + {\rm{cos}}x){\rm{d}}x} \].
Một xe ô tô đang chạy với tốc độ \[65\,{\rm{km/h}}\]thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó \[50\,{\rm{m}}\]. Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ \[v\left( t \right) = - 10t + 20\,\left( {{\rm{m/s}}} \right)\], trong đó \[t\] là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi \[S\left( t \right)\] là quãng đường ô tô đi được trong \[t\] (giây) kể từ lúc đạp phanh.
(a) Quãng đường \[S\left( t \right)\] mà xe ô tô đi được trong thời gian \[t\] (giây) là một nguyên hàm của hàm số \[v\left( t \right)\].
(b) \[S\left( t \right) = - 5{t^2} + 20t\].
(c) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 20 giây.
(d) Xe ô tô đó không va chạm vào chướng ngại vật trên đường.
Một bể chứa dầu ban đầu có \(50000\)lít dầu. Gọi \(V\left( t \right)\) là thể tích dầu (lít) trong bể tại thời điểm \(t\), trong đó \(t\)tính theo giờ \(0 \le t \le 24\). Trong quá trình bơm dầu vào bể, thể tích dầu tăng theo tốc độ được biểu diễn bởi hàm số \(V'\left( t \right) = k.\sqrt t \), với \(k\)là hằng số dương. Sau 4 giờ bơm liên tục, thể tích dầu trong bể đạt \(58000\) lít.
(a) Hàm số \(V\left( t \right)\) là một nguyên hàm của hàm số \(f\left( t \right) = k.\sqrt t \).
(b)\(V\left( t \right) = \frac{{2k}}{3}.t\sqrt t + C\), với \(0 \le t \le 24\)và \(k,\,\,C\)là các hằng số.
(c) Sau 16 giờ bơm liên tục, thể tích dầu trong bể đạt được \(148000\)lít.
(d) Trong quá trình bơm dầu, nếu sau mỗi giờ lượng dầu bị rò rỉ đều đặn với tốc độ \(500\)lít/giờ, thì tại thời điểm \(t\) bằng 9 giờ, thể tích dầu trong bể là \(72.500\) lít.
Hai công ty, công ty A và công ty B, cùng ra mắt sản phẩm cạnh tranh thị trường mới vào cùng thời điểm. Thị phần được đo bằng số lượng khách hàng lũy kế.
Công ty A: Bắt đầu với 0 khách hàng. Trong giai đoạn đầu, chiến dịch marketing hiệu quả giúp tốc độ thu hút khách hàng mới của họ tăng dần theo thời gian, được mô tả bởi hàm \(f\left( t \right) = 2t + 7\) (nghìn khách hàng/tháng), với \(t\) là số tháng kể từ khi ra mắt.
Công ty B: Nhờ có uy tín từ trước, họ bắt đầu với 10 nghìn khách hàng đặt trước sản phẩm. Sau đó, họ duy trì một tốc độ thu hút khách hàng mới ổn định là 10 nghìn khách hàng/tháng.
Hỏi sau khoảng bao nhiêu tháng kể từ khi ra mắt, tổng số lượng khách hàng lũy kế của công ty A bằng tổng số lượng khách hàng lũy kế của công ty B (tính cả 10 nghìn khách hàng ban đầu)?
Một hoa văn hình tròn tâm \[O,\] ngoại tiếp tam giác đều \[ABC\] có cạnh \[AB = 2\sqrt 3 \,{\rm{cm}}.\] Đường cong qua ba điểm \[A,B,C\] là một phần của parabol (xem hình vẽ).
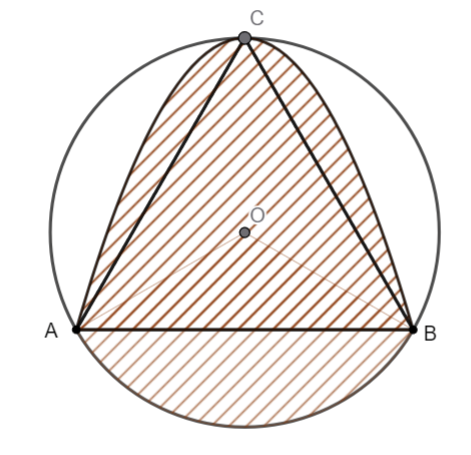
Tính diện tích của phần hình phẳng giới hạn bởi đường tròn và parabol (phần không gạch) theo đơn vị cm2 (kết quả làm tròn đến chữ số thập phân thứ hai).
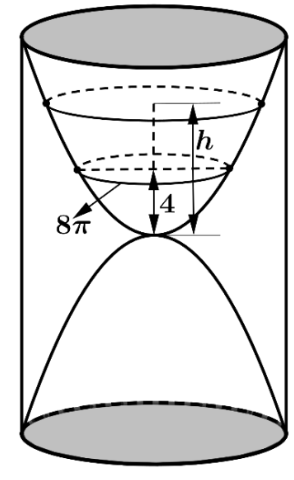
Một chiếc đồng hồ cát như hình vẽ gồm hai phần đối xứng nhau qua mặt phẳng nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt phẳng nằm ngang. Ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao của mực cát bằng \(\frac{2}{3}\) chiều cao của bên đó (xem hình vẽ). Cát chảy từ trên xuống dưới với tốc độ \(v\left( t \right) = 0,2t + 13\,\) (cm3/phút). Khi chiều cao của cát còn 4cm thì bề mặt trên cùng của cát tạo thành một đường tròn có chu vi bằng \(8\pi \)cm. Biết sau 20 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài bằng bao nhiêu centimet? (Nếu kết quả là số thập phân thì làm tròn đến hàng đơn vị).