Bài tập ôn tập Toán 12 Cánh diều Chương 4 có đáp án
55 câu hỏi
A. Trắc nghiệm
Dạng 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[f\left( x \right) = 3 + \frac{1}{x}\]. Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của \[f\left( x \right)\] trên \[\left( {0; + \infty } \right)\]?
\({F_1}\left( x \right) = 3x - \frac{1}{{{x^2}}}\).
\({F_2}\left( x \right) = 3x + \ln x\).
\({F_3}\left( x \right) = 3x + \frac{1}{{{x^2}}}\).
\({F_4}\left( x \right) = 3x - \ln x\).
Họ các nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + 1\) là
\({x^3} + C\).
\(\frac{{{x^3}}}{3} + x + C\).
\({x^3} + x + C\).
\(6x + C\).
Cho \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right) = \frac{2}{{x + 2}}\). Biết \(F\left( { - 1} \right) = 1\), khi đó \(F\left( 2 \right)\) bằng
\(2{\rm{ln}}3 + 2\).
\(4{\rm{ln}}2 + 1\).
\({\rm{ln}}8 + 1\).
\(2{\rm{ln}}4\).
Nguyên hàm \(F\left( x \right)\) của hàm số \[f\left( x \right) = {\left( {2x - 3} \right)^2}\] thỏa mãn \(F\left( { - 1} \right) = - 17\) là
\[\frac{{{{\left( {2x - 3} \right)}^3}}}{3} + \frac{4}{3}\].
\[\frac{4}{3}{x^3} - 6{x^2} + 9x - \frac{2}{3}\].
\[\frac{4}{3}{x^3} - 6{x^2} + 9x + \frac{8}{3}\].
\[\frac{4}{3}{x^3} - 6{x^2} + 9x + \frac{2}{3}\].
Nguyên hàm của hàm số \(f\left( x \right) = 3\cos x - 4\sin x\) là:
\(3\sin x - 4\cos x\).
\( - 3\sin x + 4\cos x\).
\(3\sin x + 4\cos x + C\).
\( - 3\sin x + 4\cos x + C\).
Nguyên hàm của hàm số \(f\left( x \right) = 2\sin x + \frac{3}{{{{\sin }^2}x}}\) là:
\[ - 2\cos x - 3\cot x + C\].
\[2\cos x - 3\tan x + C\].
\[ - 2\cos x + 3\cot x + C\].
\[2\cos x - 3\cot x + C\].
Nguyên hàm của hàm số có \[f\left( x \right) = {\tan ^2}x + {\cot ^2}x\] là:
\[2\tan x + 2\cot x + C\].
\[\frac{1}{3}{\tan ^3}x + \frac{1}{3}{\cot ^3}x + C\].
\[\tan x + \cot x - 2x + C\].
\[\tan x - \cot x - 2x + C\].
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f'\left( x \right) = 3 - 5{\rm{cos}}x\) và \(f\left( 0 \right) = 5\). Mệnh đề nào dưới đây đúng?
\(f\left( x \right) = 3x - 5{\rm{sin}}x - 5\).
\(f\left( x \right) = 3x + 5{\rm{sin}}x + 5\).
\(f\left( x \right) = 3x + 5{\rm{sin}}x + 2\).
\(f\left( x \right) = 3x - 5{\rm{sin}}x + 5\).
Cho hàm số \(f\left( x \right) = 1 + {e^x}\). Khẳng định nào dưới đây đúng?
\(\int {f\left( x \right){\rm{d}}x = x + x{e^{x - 1}} + C} \).
\(\int {f\left( x \right){\rm{d}}x = 1 + {e^x} + C} \).
\(\int {f\left( x \right){\rm{d}}x = x + {e^x} + C} \).
\(\int {f\left( x \right){\rm{d}}x = 1 + x{e^{x - 1}} + C} \).
Một nguyên hàm của hàm số \[f\left( x \right) = {2025^x}\] là
\[F\left( x \right) = x{.2025^{x - 1}}\].
\[F\left( x \right) = {2025.2024^x}\].
\[F\left( x \right) = {2025^x}.\ln 2025\].
\[F\left( x \right) = \frac{{{{2025}^x}}}{{\ln 2025}}\].
Họ tất cả các nguyên hàm của hàm số \[f\left( x \right) = {5^{2x - 1}}\] là
\[\frac{1}{2}{.5^{2x - 1}}.\ln 5 + C\].
\[{2.5^{2x - 1}}.\ln 5 + C\].
\[{5^{2x - 1}}.\ln 5 + C\].
\[\frac{1}{{2\ln 5}}{.5^{2x - 1}} + C\].
Họ nguyên hàm của hàm số \(f\left( x \right) = {4^x} + \cos 2x\) là
A. \(\frac{{{4^x}}}{{\ln 4}} - \frac{{\sin 2x}}{2} + C\).
B. \({4^x}\ln 4 + \frac{{\sin 2x}}{2} + C\).
C. \({4^x}\ln 4 - \frac{{\sin 2x}}{2} + C\).
D. \(\frac{{{4^x}}}{{\ln 4}} + \frac{{\sin 2x}}{2} + C\).
Tìm một nguyên hàm \[F\left( x \right)\] của hàm số \[f\left( x \right) = {e^x} - 1\] trên \[\left( { - \infty ; + \infty } \right)\], biết \[F\left( 0 \right) = 2\].
\[F\left( x \right) = \frac{1}{{{e^x}}} - x + 1\].
\[F\left( x \right) = \ln x - x - 1\].
\[F\left( x \right) = {e^x} - x + 1\].
\[F\left( x \right) = {e^x} - x + 2\].
Biết \(F\left( x \right) = {x^3}\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\). Giá trị của bằng
\(7\).
\(9\).
\(\frac{{15}}{4}\).
\(\frac{{23}}{4}\).
Giả sử \[\int\limits_0^9 {f\left( x \right){\rm{d}}x} = 7\] và \[\int\limits_9^0 {g\left( x \right){\rm{d}}x} = 1\]. Khi đó \[I = \int\limits_0^9 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]{\rm{d}}x} \] bằng
\[I = 11\].
\[I = 17\].
\[I = 23\].
\[I = 8\].
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 2 \right) - F\left( 0 \right) = 5\). Khi đó \(\int\limits_0^2 {3f} \left( x \right){\rm{d}}x\) bằng
6.
15.
10.
5.
Kết quả tích phân \(I = \int\limits_0^1 {{5^x}} {\rm{d}}x\) bằng
\(I = \frac{4}{{\ln 5}}\).
\(I = 4\ln 5\).
\(I = 5\ln 5\).
\(I = \frac{5}{{\ln 5}}\).
Giá trị của \(\int\limits_0^{\frac{\pi }{2}} {\sin x{\rm{d}}x} \) bằng
\( - 1\).
\(\frac{\pi }{2}\).
\(0\).
\(1\).
Nếu \(\int\limits_a^b {f\left( x \right){\rm{d}}x} = 2025\) thì \(\int\limits_a^b {2f\left( x \right){\rm{d}}x} \) bằng
\({2025^2}\).
\(\frac{{2025}}{2}\).
\(2023\).
\(4050\).
Nếu \(\int\limits_0^{\ln 3} {\left[ {f\left( x \right) + {e^x}} \right]{\rm{d}}x} = 6\)thì \[\int\limits_0^{\ln 3} {f\left( x \right){\rm{d}}x} \]bằng
\[6 + \ln 3\].
\[6 - \ln 3\].
\(4\).
\(8\).
Cho hàm số \(\left\{ \begin{array}{l}3{x^2}{\rm{ }} & {\rm{khi }}0 \le x \le 1\\4 - x\,{\rm{ khi }}1 \le x \le 2\end{array} \right.\). Tính tích phân \(\int\limits_0^2 {f\left( x \right){\rm{d}}x} \).
\(\frac{7}{2}\).
\(1\).
\(\frac{5}{2}\).
\(\frac{3}{2}\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2{x^2} - x\,\,\,\,\,{\rm{khi}}\,\;x < 0\\\sin x\,\,\,\;\;\quad {\rm{khi}}\,\;x \ge 0\end{array} \right..\) Tính tích phân \[\int\limits_{ - 1}^\pi {f\left( x \right){\rm{d}}x} \].
\(\frac{{13}}{6}\).
\(\frac{5}{6}\).
\( - \frac{5}{6}\).
\(\frac{{19}}{6}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\)và có đồ thị \(\left( C \right)\) là đường cong như hình dưới.
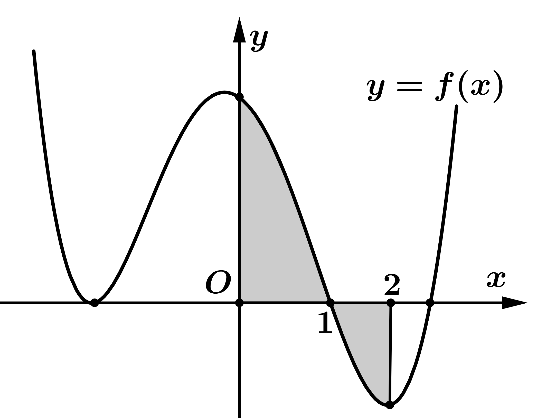
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(\left( C \right)\), trục hoành và hai đường thẳng \(x = 0;\)\(x = 2\) là
\(\int\limits_0^1 {f\left( x \right){\rm{d}}x} - \int\limits_1^2 {f\left( x \right){\rm{d}}x} \).
\(\int\limits_0^1 {f\left( x \right){\rm{d}}x} + \int\limits_1^2 {f\left( x \right){\rm{d}}x} \).
\(\left| {\int\limits_0^2 {f\left( x \right){\rm{d}}x} } \right|\).
\(\int\limits_0^2 {f\left( x \right){\rm{d}}x} \).
Diện tích hình phẳng gạch sọc trong hình vẽ dưới bằng
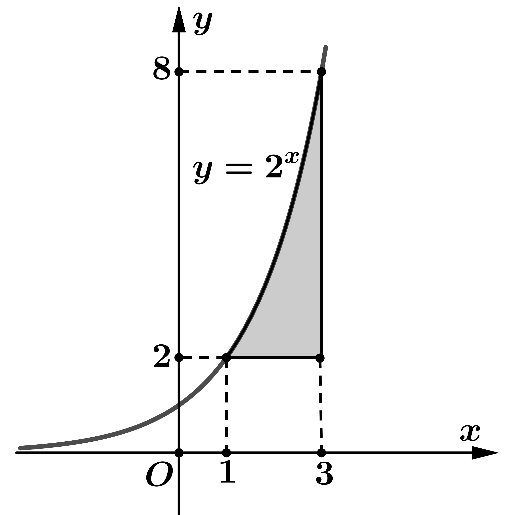
\[\int\limits_1^3 {\left( {{2^x} - 2} \right)\,{\rm{d}}x} \].
\[\int\limits_1^3 {\left( {{2^x} + 2} \right)\,{\rm{d}}x} \].
\(\int\limits_1^3 {\left( {2 - {2^x}} \right)\,{\rm{d}}x} \).
\(\int\limits_1^3 {{2^x}\,{\rm{d}}x} \).
Diện tích hình phẳng \(S\) giới hạn bởi các đường thẳng \(y = {x^2} - x,\,y = 0,\,x = 0,\,x = 2\) được tính bởi công thức nào sau đây?
\(S = \int\limits_0^2 {\left( {x - {x^2}} \right)} {\rm{d}}x.\)
\[S = \int\limits_1^2 {\left( {{x^2} - x} \right) - \int\limits_0^1 {\left( {{x^2} - x} \right){\rm{d}}x} } .\]
\(S = \int\limits_0^1 {\left( {{x^2} - x} \right) + \int\limits_1^2 {\left( {{x^2} - x} \right){\rm{d}}x} } .\)
\(S = \int\limits_0^2 {\left( {{x^2} - x} \right)} {\rm{d}}x.\)
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = {\left( {x - 2} \right)^2} - 1\], trục hoành và hai đường thẳng \[x = 1,\,x = 2\] bằng
\[\frac{2}{3}\].
\[\frac{7}{3}\].
\[\frac{1}{3}\].
\[\frac{3}{2}\].
Cho hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2}\) và đường thẳng \(y = 4\) quay quanh trục \[Ox\].
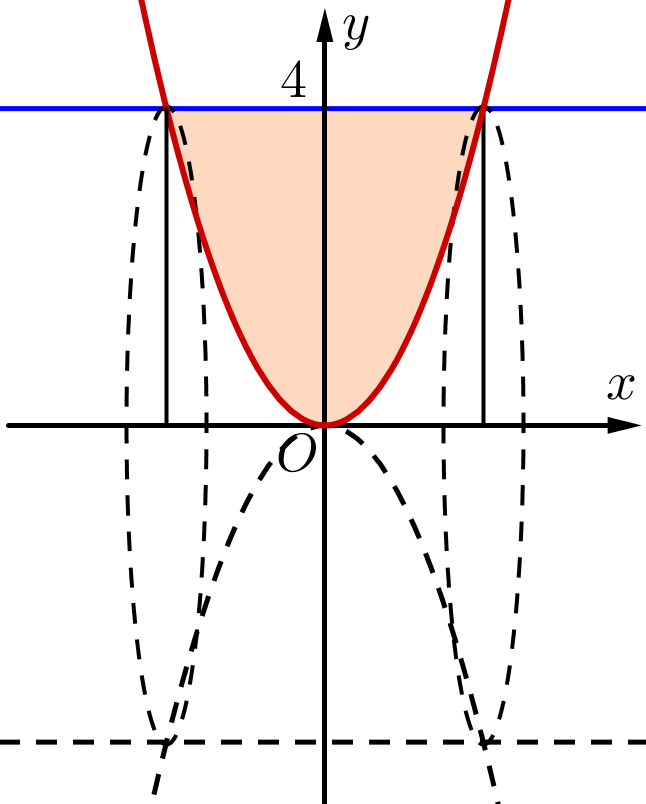
Thể tích khối tròn xoay sinh ra bằng:
\(\frac{{64\pi }}{5}\).
\(\frac{{128\pi }}{5}\).
\(\frac{{256\pi }}{5}\).
\(\frac{{152\pi }}{5}\).
Tính thể tích chứa được của một cái chậu inox to mà khách hàng đặt theo kích thước yêu cầu, biết phần trong của nó có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đường \[y = \sqrt x + 1\], trục \[Ox\] và các đường thẳng \[x = 0,\,\,x = 2\]quanh trục \[Ox\], đơn vị trên trục là decimet (làm tròn kết quả đến hàng phần trăm).
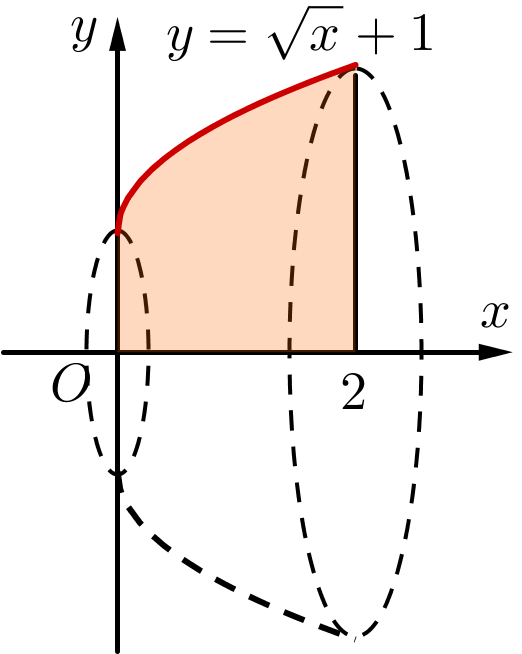
12,12\[{\rm{d}}{{\rm{m}}^3}\].
12,21 \[{\rm{d}}{{\rm{m}}^3}\].
24,14 \[{\rm{d}}{{\rm{m}}^3}\].
24,41 \[{\rm{d}}{{\rm{m}}^3}\].
Tính thể tích \(V\) của phần vật thể giới hạn bởi hai mặt phẳng \(x = 0,\,x = 1\), có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\,\left( {0 \le x \le 1} \right)\) là một tam giác đều có cạnh bằng \(x\).
\(V = \frac{{12\pi }}{5}.\)
\(V = \frac{{12}}{5}\).
\(V = \frac{{\sqrt 3 \pi }}{{12}}.\)
\(V = \frac{{\sqrt 3 }}{{12}}.\)
Cho hình phẳng giới hạn bởi đường cong \(y = \sqrt {x + 2} \) và hai trục toạ độ. Thể tích khối tròn xoay thu được khi quay hình phẳng đó quanh trục \(Ox\) bằng
\[\frac{{4\sqrt 2 }}{3}.\]
\[2.\]
\[2\pi .\]
\[\frac{{4\sqrt 2 }}{3}\pi .\]
Dạng 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Giả sử chi phí mua và bảo trì một thiết bị trong \(x\) năm có thể được mô hình hóa theo công thức \(C = 5000\left( {25 + 3\int\limits_0^x {{t^{\frac{1}{4}}}{\rm{d}}t} } \right)\) (đồng).
(a) Chi phí mua 1 sản phẩm là 100 000 đồng.
(b) Chi phí bảo trì năm đầu tiên của 1 sản phẩm là \(12\,000\)đồng.
(c) Sau 6,5 năm thì số tiền mua một sản phẩm bằng số tiền bảo trì sản phẩm đó.
(d) Nếu một nhà đầu tư có 10 triệu đồng, thì họ có thể mua và bảo trì tối đa 30 sản phẩm trong 10 năm.
Trong thí nghiệm nuôi cấy một loại vi sinh vật, kí hiệu \(f\left( t \right)\) là tổng số lượng vi sinh vật sau \(t\) giờ. Biết rằng sau 3 giờ đầu tiên thì tổng số lượng vi sinh vật là 50 con. Trong 7 giờ tiếp theo, số lượng vi sinh vật thay đổi với tốc độ \(f'\left( t \right) = {t^2} - 8t\) (con/giờ).
(a) Họ nguyên hàm của \(f'\left( t \right)\) là \(\frac{{{t^3}}}{3} - 8{t^2} + C\)\(\left( {C \in \mathbb{R}} \right)\).
(b) Số lượng vi khuẩn tăng liên tục trong khoảng từ 3 giờ đến 10 giờ sau thời điểm làm thí nghiệm.
(c) Số lượng vi khuẩn là nhỏ nhất sau 8 giờ tính từ lúc bắt đầu làm thí nghiệm.
(d) Sau 6 giờ thì số lượng vi khuẩn là 5 con.
Một quả cầu lông được đánh lên từ độ cao \[2,2\,{\rm{m}}\] với vận tốc được tính bởi công thức sau đây \[v\left( t \right) = - \,0,8\,t + 4,16\,\,\left( {{\rm{m/s}}} \right)\].
(a) Công thức tính độ cao của quả cầu theo \[t\] là \[h\left( t \right) = - \,0,4\,{t^2} + 4,16t + \,2,2\,\left( {\rm{m}} \right)\].
(b) Quả cầu đạt độ cao cao nhất tại thời điểm \[t = 5,2\,\left( {\rm{s}} \right)\].
(c) Độ cao cao nhất của quả cầu bằng \[13,016\,\,\left( {\rm{m}} \right)\].
(d) Thời điểm quả cầu chạm đất là \[t = 10,5\,\,\left( {\rm{s}} \right)\].
Một ô tô đang chạy với vận tốc \(18\,\,\left( {{\rm{m/s}}} \right)\) thì người lái hãm phanh. Sau khi hãm phanh ô tô chuyển động chậm dần đều với vận tốc \[v\left( t \right) = 18 - 36t\,\,\left( {{\rm{m/s}}} \right)\], trong đó \(t\) là khoảng thời gian được tính bằng giây kể từ lúc ô tô bắt đầu hãm phanh.
(a)Thời gian kể từ lúc hãm phanh đến lúc xe dừng hẳn là \(1,5\) giây.
(b)Quãng đường xe đi được sau \(0,3\) giây kể từ lúc hãm phanh là \(3\) mét.
(c)Quãng đường kể từ lúc hãm phanh đến lúc xe dừng hẳn là \(4,5\) mét.
(d)Gia tốc tức thời của chuyển động này là \(36\,\,\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\).
Chất điểm chuyển động theo quy luật vận tốc \[v\left( t \right)\left( {{\rm{m/s}}} \right)\] có dạng đường thẳng khi \[0 \le t \le 3\left( {\rm{s}} \right)\] và \[8 \le t \le 15\left( {\rm{s}} \right)\]và \[v\left( t \right)\] có dạng đường Parabol khi \[3 \le t \le 8\left( {\rm{s}} \right)\](như hình vẽ).
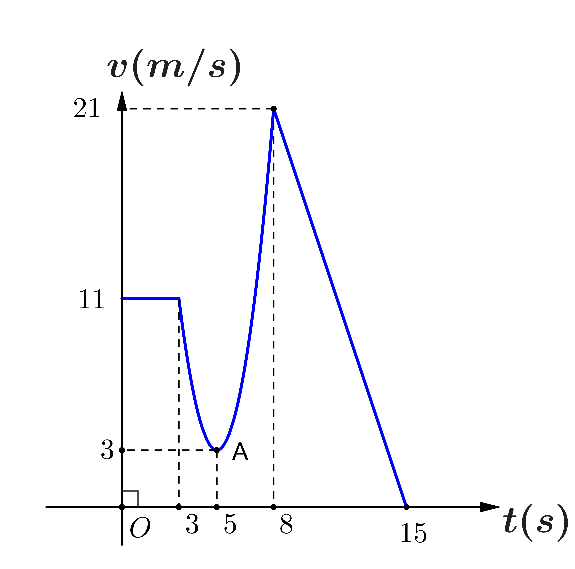
(a) Vận tốc của chất điểm tại thời điểm \(t = 15\) là \(v\left( {15} \right) = 21\,\left( {{\rm{m/s}}} \right)\).
(b) Quãng đường chất điểm di chuyển được trong \(3\) giây đầu tiên là: \[{S_1} = \int\limits_0^3 {11{\rm{d}}t} \,\left( {\rm{m}} \right)\].
(c) Quãng đường chất điểm đi được trong khoảng thời gian từ \(8\)giây đến \(15\) giây bằng \(73,5\left( {\rm{m}} \right).\)
(d) Vận tốc trung bình \({v_{tb}}\) của chất điểm trong khoảng thời gian từ \(3\) đến \(8\) giây thỏa mãn \({v_{tb}} < 7\,\,\left( {{\rm{m/s}}} \right)\).
Một người điều khiển xe Taxi xuất phát từ trạm thu phí muốn nhập làn vào đường cao tốc, chuyển động tăng tốc với tốc độ \(v\left( t \right) = \frac{1}{{180}}{t^2} + \frac{{116}}{{135}}t\left( {{\rm{m/s}}} \right)\)(trong đó, \(t\)là thời gian tính bằng giây kể từ khi Taxi chuyển động rời trạm thu phí). Từ trạm thu phí đó, một xe Cứu thương cũng xuất phát, chuyển động thẳng cùng hướng với xe Taxi nhưng chậm hơn 1 giây so với xe Taxi và có gia tốc bằng \(a\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)(\(a\) là hằng số). Sau khi xe Cứu thương xuất phát được \(17\)giây thì đuổi kịp xe Taxi. Biết rằng, xe Taxi nhập làn cao tốc sau 20 giây và cả hai xe duy trì sự tăng tốc trong \(28\) giây kể từ khi Taxi rời trạm thu phí.
(a) Quãng đường (kết quả làm tròn đến hàng đơn vị) xe Taxi đi được từ trạm thu phí đến khi nhập làn khoảng \(187\,{\rm{m}}\).
(b) Xe cứu thương chuyển động với gia tốc \(a = \frac{{300}}{{289}}\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\).
(c) Vận tốc (kết quả làm tròn đến hàng đơn vị) của xe Cứu thương tại thời điểm đuổi kịp xe Taxi khoảng \(16\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\).
(d) Trong khoảng thời gian kể từ lúc hai xe gặp nhau cho đến giây thứ \(28\)(kể từ khi Taxi chuyển động rời trạm thu phí) vận tốc trung bình của xe Cứu thương lớn hơn vận tốc trung bình của xe Taxi.
Cho hàm số \[f\left( x \right) = {x^3} - 3{x^2} + 2x\] có đồ thị như hình vẽ.
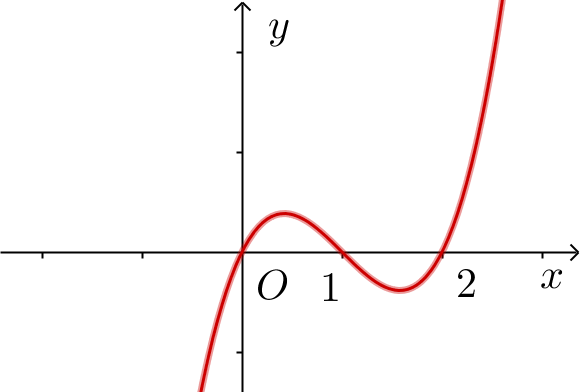
(a) \[\int\limits_0^1 {f'\left( x \right)\,} {\rm{d}}x = 0\].
(b) Gọi \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right)\], khi đó \[F\left( x \right) = \int {f'\left( x \right)} \,{\rm{d}}x\].
(c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục hoành và hai đường thẳng \[x = 0,x = 2\] là \[\int\limits_0^2 {f\left( x \right)} \,{\rm{d}}x\].
(d) Gọi \[\left( D \right)\] là hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục hoành, trục tung và đường thẳng \[x = 1\]. Thể tích khối tròn xoay được tạo thành khi quay \[\left( D \right)\] quanh trục hoành được tính theo công thức \[\pi \int\limits_0^1 {{f^2}\left( x \right)} \,{\rm{d}}x\].
Cho một viên gạch men có dạng hình vuông \(OABC\) như hình vẽ. Sau khi tọa độ hóa, ta có \(O\left( {0\,;\,0} \right)\), \(A\left( {0\,;\,1} \right)\), \(B\left( {1\,;\,1} \right)\), \(C\left( {1\,;\,0} \right)\) và hai đường cong lần lượt là đồ thị hàm số \(y = {x^3}\) và \(y = \sqrt[3]{x}.\)
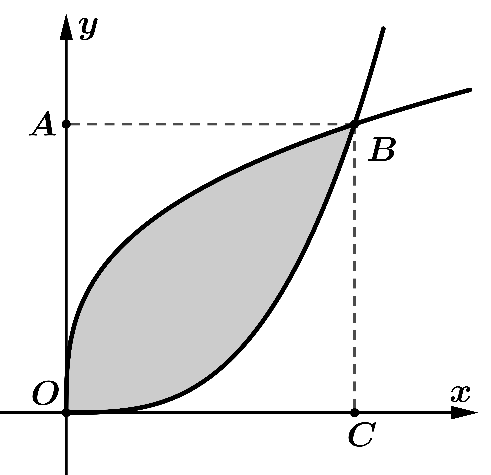
(a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt[3]{x}\), trục \(Ox\), đường thẳng\(x = 0\) và đường thẳng \(x = 1\) được tính bằng công thức \(S = \int\limits_0^1 {\left| {\sqrt[3]{x}} \right|} \,{\rm{d}}x\).
(b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục \(Ox\),đường thẳng \(x = 0\) và đường thẳng \(x = 1\) có giá trị bằng \(\frac{3}{4}\)(đvdt).
(c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\) và \(y = \sqrt[3]{x}\), đường thẳng\(x = 0\) và đường thẳng \(x = 1\) được tính bằng công thức \[S = \int\limits_0^1 {\left( {{x^3} - \sqrt[3]{x}} \right){\rm{d}}x} \].
(d) Diện tích phần không được tô đậm trên viên gạch men có giá trị bằng \(\frac{1}{2}\)(đvdt).
Người ta chế tác một giọt nước bằng thủy tinh. Biết giọt nước thủy tinh này là vật thể tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \[f\left( x \right) = \left\{ \begin{array}{l}\sqrt {4 - {x^2}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( { - 2 \le x \le 0,6} \right)\\ - \frac{{\sqrt {91} }}{{20}}x + \frac{{23\sqrt {91} }}{{100}}\,\,\,\,\left( {0,6 < x \le 4,6} \right)\end{array} \right.\] và trục \[Ox\] quanh trục \[Ox\] (đơn vị trên trục là centimet).

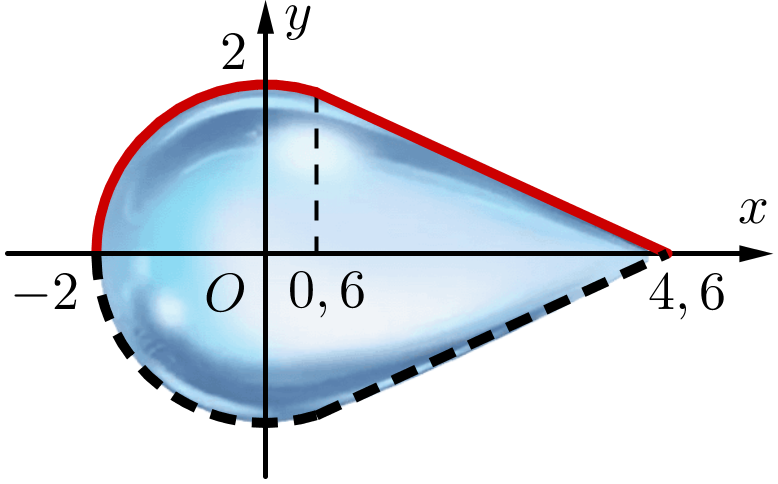
(a) Hàm số \[y = f\left( x \right)\] liên tục tại \[x = 0,6\].
(b) Diện tích mặt cắt của giọt nước thủy tinh khi cắt bởi mặt phẳng qua trục được tính bởi công thức \[S = 2\int\limits_{ - 2}^{4,6} {f\left( x \right){\rm{d}}x} \] cm2.
(c) Thể tích của giọt nước thủy tinh này lớn hơn 40 cm3.
(d) Biết khối lượng riêng của thủy tinh là \[\rho = 2,6\] g/cm3, khối lượng của giọt nước thủy tinh này là 102,22 g (làm tròn kết quả đến hàng phần trăm).
Một cái trứng khủng long đồ chơi là một khối tròn xoay được tạo thành từ 2 mảnh ghép lại. Biết mảnh trên được tạo thành khi xoay một phần tư đường elip với trục lớn là 8 và trục nhỏ là 4 quanh trục \[Ox\]và mảnh dưới được tạo thành khi xoay một phần tư đường tròn bán kính 2 quanh trục \[Ox\] như hình sau (bỏ qua độ dày của vỏ trứng).


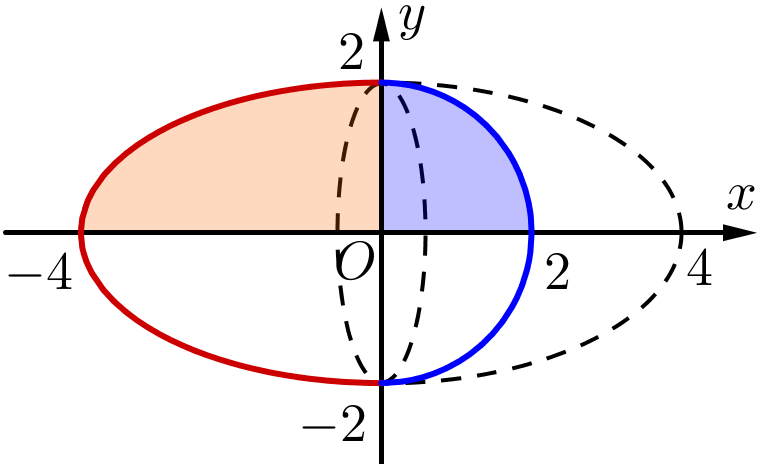
(a) Thể tích phần trong của mảnh trên được tính bởi \[{V_1} = \frac{\pi }{4}\int\limits_{ - 4}^0 {\left( {16 - {x^2}} \right){\rm{d}}x} \].
(b) Thể tích phần trong của mảnh trên gấp 2 lần thể tích phần trong của mảnh dưới.
(c) Thể tích phần trong của quả trứng đồ chơi này là \[16\pi \].
(d) Diện tích thiết diện khi cắt bởi mặt phẳng qua trục của quả trứng là \[3\pi \].
Dạng 3. Trắc nghiệm trả lời ngắn
Một bác thợ xây bơm nước vào bể chứa nước. Gọi \(h\left( t \right)\) là thể tích nước bơm được sau \(t\) giây. Cho \(h'\left( t \right) = 6a{t^2} + 2bt\) và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là \(90{\rm{\;}}{{\rm{m}}^3}\) và sau 6 giây thì thể tích nước trong bể là \(504{\rm{\;}}{{\rm{m}}^3}\). Tính thể tích nước trong bể sau khi bơm được 9 giây (đơn vị: m3).
Cửa hàng thực phẩm của anh An có lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức \(P'\left( x \right) = - 0,01x + 2\). Lợi nhuận của sản phẩm trên khi doanh số là 200 với sản phẩm lớn hơn doanh số 150 sản phẩm là bao nhiêu triệu đồng, biết \(P\left( x \right)\) là lợi nhuận tính bằng triệu đồng?
Tốc độ tăng trưởng của một đàn gấu mèo tại thời điểm \(t\) tháng kể từ khi người ta thả 100 cá thể đầu tiên vào một khu rừng được ước lượng bởi công thức \(P'\left( t \right) = 8t + 30\) (con/tháng), với \(P\left( t \right)\) là số lượng cá thể trong đàn tại thời điểm \(t\) tháng tương ứng. Dựa vào tốc độ tăng trưởng đã cho, hãy ước tính số cá thể của đàn gấu mèo này tại thời điểm 3 tháng kể từ khi chúng được thả vào rừng.
Tốc độ\(v\left( {{\rm{\;km}}/{\rm{ph\'u t}}} \right)\) của một ca nô cao tốc thay đổi theo thời gian \(t\) (phút) như đồ thị ở hình vẽ sau:
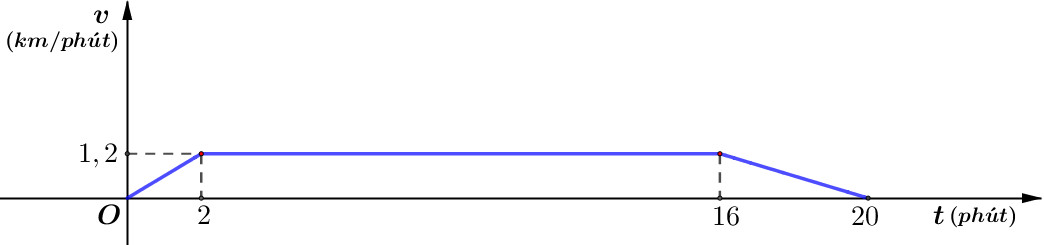
Tính tốc độ trung bình của ca nô trong khoảng thời gian 20 phút đầu tiên (đơn vị: km/phút).
Chị Hồng đang lái xe với vận tốc \(5{\rm{\;m}}/{\rm{s}}\) thì nhận thấy phía trước đèn giao thông đang chuẩn bị chuyển sang đèn đỏ nên cần giảm tốc độ của xe để đợi đèn đỏ. Sau khi đạp phanh, xe chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 0,5t + 5\left( {{\rm{\;m}}/{\rm{s}}} \right)\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi xe dừng hẳn, xe di chuyển quãng đường bao nhiêu mét?
Để trang trí cho một phòng trong một tòa nhà, người ta vẽ lên tường một hình như sau: trên mỗi cạnh của hình lục giác đều có cạnh bằng 2 dm có một cánh hoa hình parabol, đỉnh của parabol cách cạnh 3 dm và nằm phía ngoài hình lục giác, đường parabol đó đi qua hai đầu mút của mỗi cạnh (xem hình sau). Hãy tính diện tích của hình nói trên (kể cả hình lục giác đều) để mua sơn trang trí cho phù hợp (kết quả làm tròn đến chữ số thập phân thứ nhất sau dấu phẩy theo đơn vị decimet vuông).
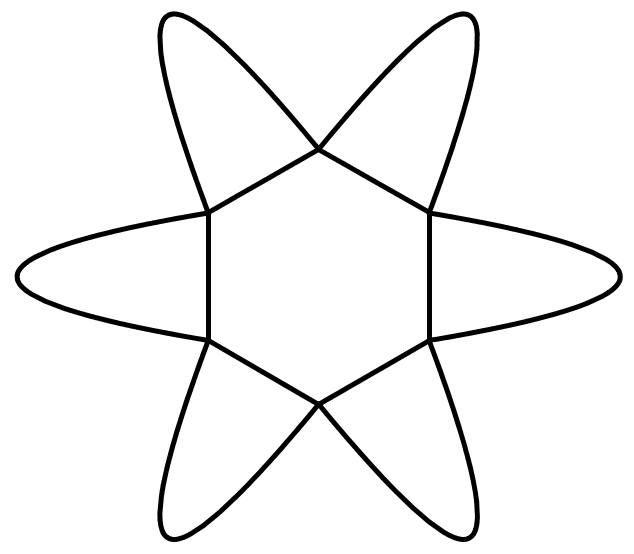
Một viên gạch hoa hình vuông cạnh \(60\)cm. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên).
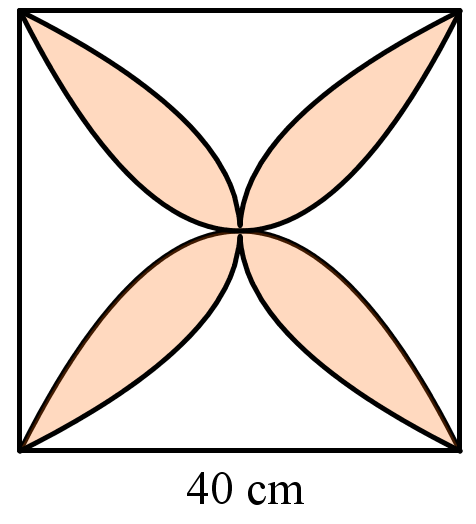
Tính diện tích phần cánh hoa của viên gạch (đơn vị: cm2).
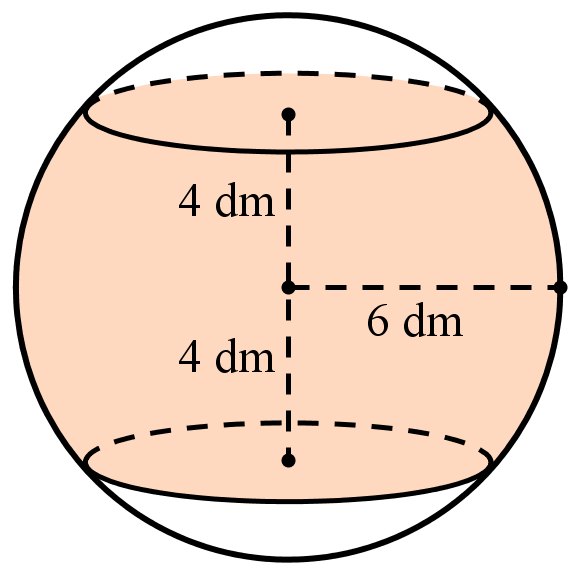
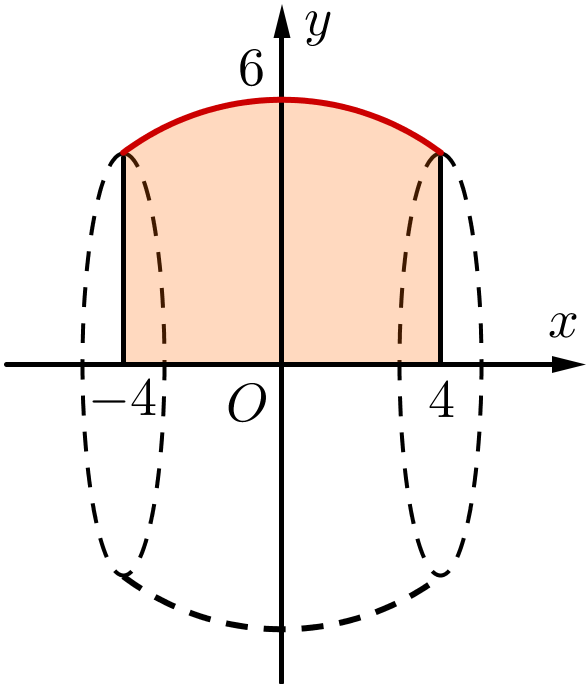
Một hình cầu có bán kính 6 dm, người ta cắt bỏ hai phần bằng hai mặt phẳng song song và cùng vuông góc với đường kính để làm mặt xung quanh của một chiếc lu chứa nước (như hình vẽ). Tính thể tích \[V\](lít) mà chiếc lu chứa được biết mặt phẳng cách tâm mặt cầu 4 dm (làm tròn đến hàng đơn vị).
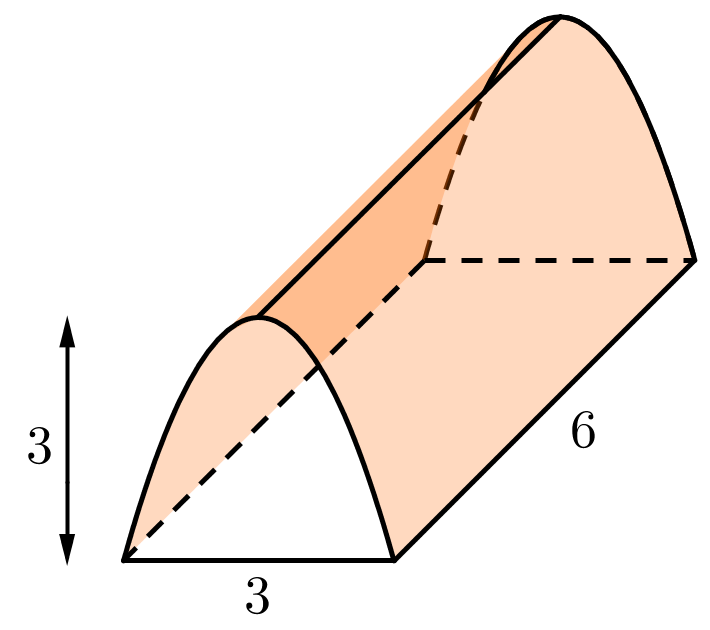
Một Chi đoàn thanh niên đi dự trại ở một đơn vị bạn, họ dự định dựng một lều trại có dạng parabol (nhìn từ mặt trước, lều trại được căng thẳng từ trước ra sau, mặt sau trại cũng là parabol có kích thước giống như mặt trước) với kích thước: nền trại là một hình chữ nhật có chiều rộng là 3 mét, chiều sâu là 6 mét, đỉnh của parabol cách mặt đất là 3 mét. Hãy tính thể tích (đơn vị: m3) phần không gian phía trong trại để cử số lượng người tham dự trại cho phù hợp.
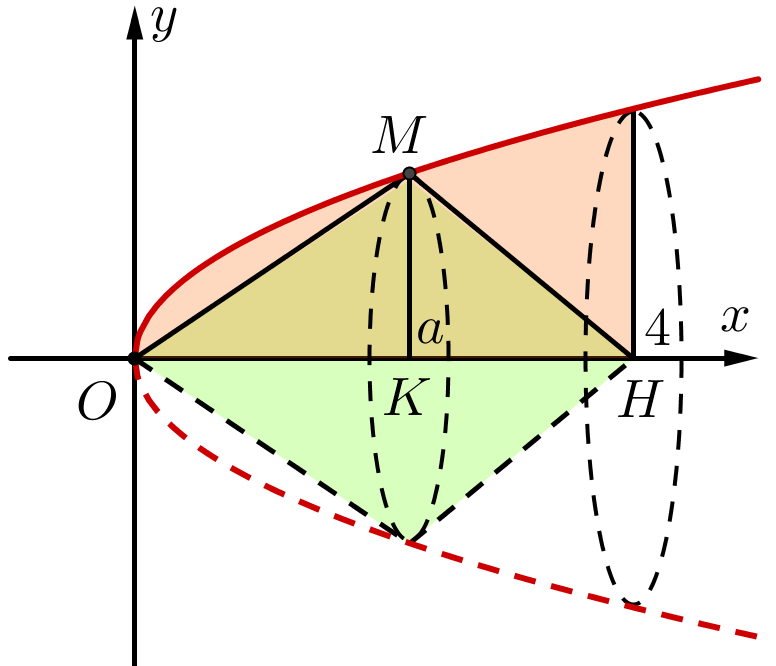
Gọi \(V\) là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x ,\)\(y = 0\) và \(x = 4\) quanh trục \(Ox\). Đường thẳng \(x = a\,\,\left( {0 < a < 4} \right)\) cắt đồ thị hàm số \[y = \sqrt x \] tại \(M\) (xem hình vẽ sau). Gọi \({V_1}\) là thể tích khối tròn xoay tạo thành khi quay tam giác \(OMH\) quanh trục \(Ox\). Biết rằng \(V = 2{V_1}\). Khi đó giá trị của \[a\] là bao nhiêu?
B. Tự luận
Tại một lễ hội dân gian, tốc độ thay đổi lượng khách tham dự được biểu diễn bằng hàm số \(B'\left( t \right) = 20{t^3} - 300{t^2} + 1000t\). Trong đó \(t\) tính bằng giờ \(\left( {0 \le t \le 15} \right)\), \(B'\left( t \right)\) được tính bằng khách/giờ. (Nguồn: A.Bigalke et al., Mathematik, Grundkurs ma-l, Cornelissen 2016). Sau một giờ, 500 người đã có mặt tại lễ hội.
(a) Viết công thức của hàm số \(B\left( t \right)\) biểu diễn số lượng khách tham dự lễ hội với \(0 \le t \le 15\).
(b) Sau 3 giờ sẽ có bao nhiêu khách tham dự lễ hội?
(c) Số lượng khách tham dự lễ hội lớn nhất là bao nhiêu?
(d) Tại thời điểm nào thì tốc độ thay đổi lượng khách tham dự lễ hội là lớn nhất?
Một vật chuyển động với vận tốc được cho bởi đồ thị ở hình vẽ dưới đây:
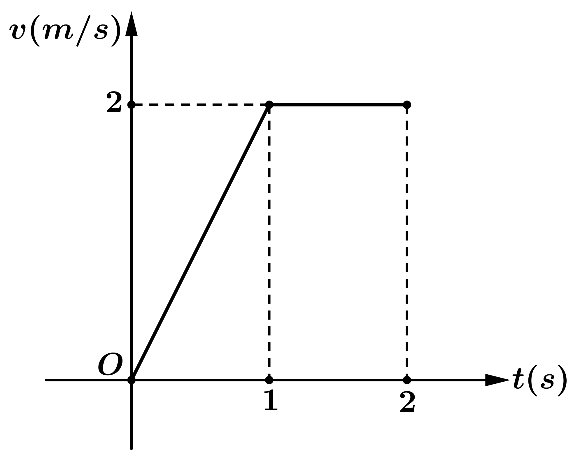
(a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên.
(b) Tính quãng đường và vật di chuyển được trong 2 giây đầu tiên.
Cho hình vẽ dưới đây là đồ thị vận tốc \(v\left( t \right)\) của một vật (\(t = 0\) là thời điểm vật bắt đầu chuyển động). Tính quãng đường chuyển động và vận tốc trung bình của vật 10 giây đầu tiên.

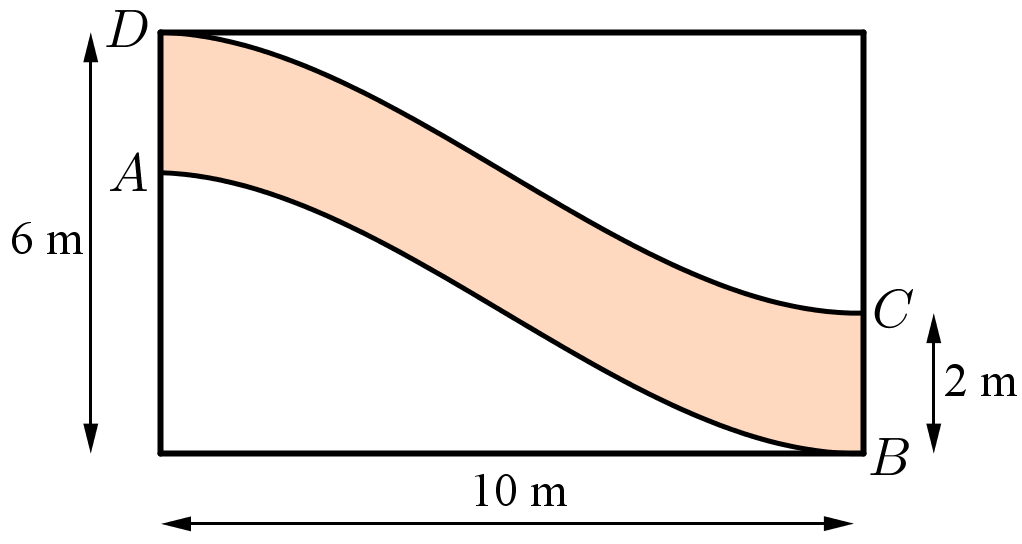
Cô Hạnh đổ bê tông một đường đi trong vườn (phần được tô màu) với kích thước được cho trong hình sau. Biết rằng đường cong \[AB\] được cho bởi đồ thị của một hàm số liên tục và đường cong \[DC\] nhận được từ đường cong \[AB\] bằng cách tịnh tiến theo phương thẳng đứng lên phía trên 2 m. Ngoài ra, cô Hạnh quyết định đổ lớp bê tông dày 15 cm và giá tiền 1 m3 bê tông là 1 080 000 đồng. Tính số tiền cô Hạnh cần dùng để đổ bê tông con đường đó.
Trên cửa sổ có dạng hình chữ nhật, họa sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong hình sau (đơn vị trên mỗi trục toạ độ là decimét).
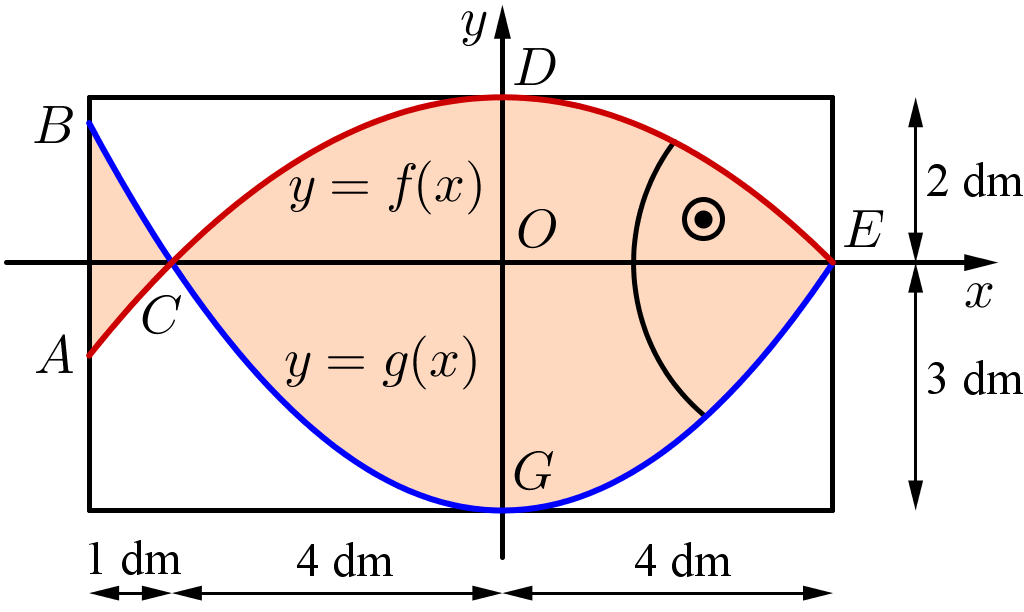
(a) Lập phương trình các parabol \[y = f\left( x \right)\] và \[y = g\left( x \right)\].
(b) Tính diện tích của logo.
(c) Logo chỉ cho phép 50% lượng ánh sáng đi qua. Lượng ánh sáng đi qua toàn bộ cửa sổ sau khi làm logo sẽ giảm bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười)?


