Đề kiểm tra Toán 11 Kết nối tri thức Chương 1 có đáp án - Đề 02
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Giải phương trình \(\sin x + 1 = 0\) ta được tập nghiệm là
\(S = \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ { - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ { - \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Rút gọn biểu thức \(M = \frac{{\sin 2x}}{{\sin x}} - \frac{{\cos 2x}}{{\cos x}}\) ta được kết quả là
\(M = \frac{1}{{\cos x}}\).
\(M = \frac{{\cos 3x}}{{\sin x.\cos x}}\).
\(M = \frac{1}{{\sin x}}\).
\(M = 1\).
Tập xác định của hàm số \(y = \cos 2x\) là
\(\left[ { - 1;1} \right]\).
\(\left[ { - 2;2} \right]\).
\(\left[ {0;1} \right]\).
\(\mathbb{R}\).
Phương trình \(\sin x = \frac{1}{5}\) có bao nhiêu nghiệm trên đoạn \(\left[ {\pi ;2\pi } \right]\)?
1.
0.
2.
Vô số.
Đồ thị hàm số \(f\left( x \right) = \sin x + 1\) đi qua điểm nào sau đây?
\(\left( {0;1} \right)\).
\(\left( {\frac{\pi }{2};0} \right)\).
\(\left( {0;2} \right)\).
\(\left( {\pi ;0} \right)\).
Hình vẽ dưới đây là đồ thị hàm số lượng giác \(y = \sin 2x\).
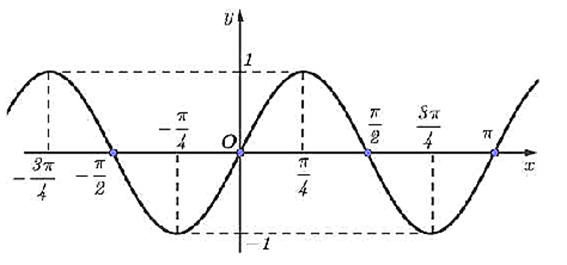
Hàm số \(y = \sin 2x\) đồng biến trên khoảng nào sau đây?
\(\left( { - \frac{{3\pi }}{4}; - \frac{\pi }{4}} \right)\).
\(\left( {\frac{\pi }{4};\frac{\pi }{2}} \right)\).
\(\left( { - \frac{\pi }{4};\frac{\pi }{4}} \right)\).
\(\left( {0;1} \right)\).
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho biểu thức \(A = {\left( {\sin x - \cos x} \right)^2}\).
Khi \(x = 0\) thì \(A = 1\).
\(A = 1 + \sin 2x\).
\(A \in \left[ {0;2} \right]\).
Nếu \(\cos 2x = - 1\) thì \[A = - 2\].
Cho hàm số \(g\left( x \right) = \sin x + \cos x\).
\(g\left( x \right) = \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right),\forall x \in \mathbb{R}\).
Với \(\forall x \in \left( {\pi ;\frac{{3\pi }}{2}} \right)\) thì \(g\left( x \right) < 0\).
Phương trình \(g\left( x \right) = 0\) có hai nghiệm thuộc đoạn \(\left[ {0;2\pi } \right]\).
Giá trị lớn nhất của hàm số \(g\left( x \right)\) bằng 2.
Phần 3. Trắc nghiệm trả lời ngắn
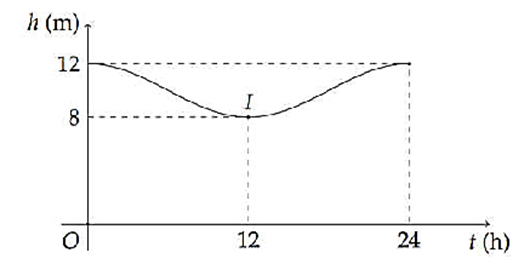
Mực nước cao nhất tại một cảng biển là 12 m khi thủy triểu lên cao và sau 12 giờ khi thủy triều xuống thấp thì mực nước thấp nhất là 8 m. Đồ thị dưới đây mô tả sự thay đổi chiều cao của mực nước tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước h (m) theo thời gian t (h) (\(0 \le t \le 24\)) được cho bởi công thức \(h = m + a\cos \left( {\frac{\pi }{{12}}t} \right)\) với m; a là các số thực dương cho trước. Giá trị của \(T = m \cdot a\) là bao nhiêu?
Nghiệm dương nhỏ nhất của phương trình \(\sin \left( {2x + \frac{\pi }{3}} \right) = \sin x\) là \({x_0} = \frac{m}{n}\pi \) với \(\frac{m}{n}\) là phân số tối giản, \(m,n \in \mathbb{N}*\). Tính giá trị của biểu thức \(m + 2n\).
Cho \(\sin \alpha = \frac{1}{5}\) và \(\frac{\pi }{2} < \alpha < \pi \). Biết \(\cot 2\alpha = - \frac{{a\sqrt 6 }}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Giá trị của \(a + b\) bằng bao nhiêu?


