Đề kiểm tra Toán 11 Kết nối tri thức Chương 1 có đáp án - Đề 01
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho góc lượng giác α thỏa mãn \(\sin \alpha = - \frac{4}{5}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\cos \alpha \)bằng
\( - \frac{3}{5}\).
\( - \frac{3}{{25}}\).
\(\frac{9}{{25}}\).
\(\frac{3}{5}\).
Cho \(\sin \alpha = \frac{2}{5}\). Khi đó \(\cos 2\alpha \) bằng
\(\frac{{17}}{{25}}\).
\(\frac{{17}}{5}\).
\( - \frac{3}{5}\).
\(\frac{3}{5}\).
Đường cong trong hình sau đây là đồ thị của hàm số \(y = \sin x\) trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\):
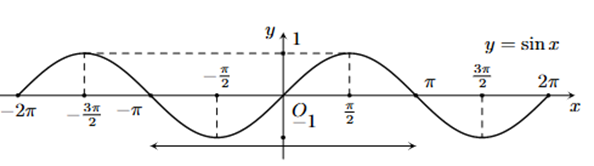
Khẳng định nào dưới đây sai?
Hàm số \(y = \sin x\) là hàm số tuần hoàn với chu kì \(T = 2\pi \).
Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Hàm số \(y = \sin x\) có tập giá trị là \(\left[ { - 1;1} \right]\).
Hàm số \(y = \sin x\) là hàm số chẵn.
Tập xác định của hàm số \(y = \cot x\) là
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k2\pi |k \in \mathbb{Z}} \right\}\).
Nghiệm của phương trình \(\sin x = 1\) là
\(x = k\pi ,k \in \mathbb{Z}\).
\(x = k2\pi ,k \in \mathbb{Z}\).
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\).
Trong các công thức lượng giác dưới đây, công thức nào đúng.
\(\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\).
\(\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 - \tan a\tan b}}\).
\(\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{\tan a\tan b}}\).
\(\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{\tan a + \tan b}}\).
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho góc lượng giác α thỏa mãn \(\tan \alpha = 3\).
\(\cot \alpha = \frac{1}{3}\).
\(\tan \left( {\alpha + 3\pi } \right) = 3 + 3\pi \).
\(\tan \left( { - \alpha } \right) = - 3\).
\(\cot 2\alpha = - \frac{4}{3}\).
Cho hàm số \(y = f\left( x \right) = \cos \left( { - x} \right)\) xác định trên tập D.
Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi } \right\},k \in \mathbb{Z}\).
\(y = - \cos x,\forall x \in D\).
\(f\left( x \right) = 1 \Leftrightarrow x = k2\pi ,k \in \mathbb{Z}\).
Tổng các nghiệm của phương trình \(f\left( x \right) = 1\) trên khoảng \(\left[ { - \pi ;6\pi } \right]\) là \(12\pi \).
Phần 3. Trắc nghiệm trả lời ngắn
Nghiệm dương nhỏ nhất của phương trình \(\cos \left( {\frac{\pi }{4} - x} \right) + 1 = 0\) có dạng \(x = \frac{a}{b}\pi \) với \(\frac{a}{b}\) là phân số tối giản. Tính \(T = a + b\).
Hằng ngày mực nước của con kênh lên xuống theo thủy triều, độ sâu L (tính theo đơn vị mét) của mực mước trong kênh theo thời gian t (giờ) được cho bởi công thức \(L = 3\sin \left( {\frac{{\pi t}}{4} + \frac{\pi }{3}} \right) + 14\). Thời gian ngắn nhất để mực nước của kênh cao nhất là \(t = \frac{a}{b}\) (giờ) với \(\frac{a}{b}\) là phân số tối giản. Tính giá trị của \(a \cdot b\).
Cho góc lượng giác \(x \in \left( {\frac{\pi }{2};\pi } \right)\) và có \(\sin x = \frac{1}{3}\). Tính giá trị biểu thức \(A = \cos \left( {\frac{\pi }{4} - x} \right)\) (làm tròn kết quả đến hàng phần chục).


