Đề kiểm tra Toán 11 Chân trời sáng tạo Chương 3 có đáp án - Đề 2
11 câu hỏi
Kết quả giới hạn \(\mathop {\lim }\limits_{x \to 1} \left( {4x + 2} \right)\) là
\(1\).
\(5\).
\(6\).
\(2\).
Cho hàm số \(f\left( x \right) = \frac{{x + 3}}{{x - 1}}\). Hàm số gián đoạn tại điểm nào?
Hàm số gián đoạn tại \(x = 1\).
Hàm số gián đoạn tại \(x = 3\).
Hàm số gián đoạn tại \(x = - 1\).
Hàm số gián đoạn tại \(x = - 3\).
Cho hàm số \(f\left( x \right) = \frac{{{x^2} + 3x + 2}}{{x - 2}}\). Hàm số liên tục trên khoảng nào sau đây?
\(\mathbb{R}\).
\(\left( { - 3; + \infty } \right)\).
\(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
Cho hai dãy \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) thỏa mãn \(\lim {u_n} = 2\) và \(\lim {v_n} = 3\). Giá trị của \(\lim \left( {{u_n}{v_n}} \right)\) bằng
\(5\).
\(6\).
\( - 1\).
\(1\).
\(\lim \frac{{2{n^2} - 3}}{{{n^6} + 5{n^5}}}\) bằng
\(2\).
\(0\).
\( - \frac{3}{5}\).
\( - 3\).
Hàm số \(y = {x^2} + \sqrt {x - 2} \) gián đoạn tại điểm nào sau đây?
\({x_0} = 4\).
\({x_0} = 0\).
\({x_0} = 2\).
\({x_0} = 3\).
Cho hàm số \(f\left( x \right) = \frac{{\sqrt {x + 1} - 2}}{{x - 3}}\).
\(f\left( 8 \right) = - \frac{1}{5}\).
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \frac{1}{3}\).
\(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \frac{1}{6}\).
Biết \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = a,\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 2} - x} \right) = b\). Khi đó \(3a + 4b = 2\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{1}{4}x + \frac{1}{4}\;\;\;\;\;\;\;\;{\rm{khi}}\;\;x \le 2\\\frac{{\sqrt {3x - 2} - 2}}{{x - 2}}\;\;{\rm{khi}}\;\;x > 2\end{array} \right.\).
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \frac{1}{2}\).
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \frac{1}{4}\).
Hàm số \(f\left( x \right)\) liên tục tại \(x = 2\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \frac{3}{4}\).
Tính giới hạn \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \frac{{1 - \sqrt {x + 3} }}{{x + 2}}\).
Tìm \(a\) để \(\lim \frac{{a{n^3} + {n^2} - 4}}{{2{n^3} + 1}} = - 2\).
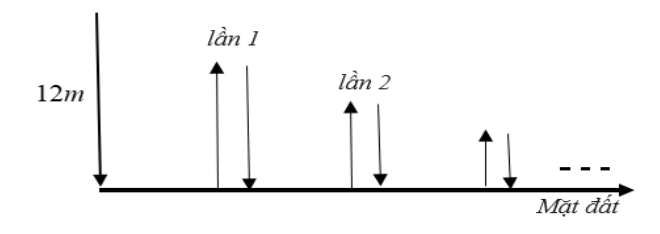
Bạn An thả một quả bóng cao su từ độ cao 12 mét so với mặt đất. Mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng \(\frac{2}{3}\) độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tính tổng quãng đường của quả bóng mà bạn An thả đã di chuyển (từ lúc thả bóng cho tới khi quả bóng không nảy nữa)? (tham khảo hình vẽ bên dưới).