Bài tập ôn tập Toán 11 Chân trời sáng tạo Chương 3 có đáp án
55 câu hỏi
\(\lim \frac{1}{{{n^4}}}\) bằng
2.
4.
0.
3.
Cho hàm số \(f\left( x \right) = \frac{{2x - 1}}{{x - 2}}\). Kết luận nào sau đây đúng?
Hàm số liên tục trên \(\left[ { - 2;2} \right]\).
Hàm số liên tục trên \(\left( {0;4} \right)\).
Hàm số liên tục tại \[x = 2\].
Hàm số liên tục tại \[x = 1\].
Hàm số nào dưới đây liên tục trên \(\mathbb{R}\).
\(y = \sqrt x \).
\(y = \tan x\).
\(y = 3{x^3} - 4{x^2} + 1\).
\(y = \cot x\).
Giới hạn \(\lim \frac{{\sqrt n }}{{2{n^2} + 3}}\) có kết quả là
\(\frac{1}{2}\).
0.
\(\frac{1}{5}\).
\( - \frac{3}{2}\).
Trong các mệnh đề sau, mệnh đề nào sai?
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{{x^4}}} = + \infty \).
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt x }} = + \infty \).
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{x - 2}} = + \infty \).
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{x - 2}} = - \infty \).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {c;d} \right)\). Điều kiện cần và đủ để hàm số liên tục trên \(\left[ {c;d} \right]\) là
\(\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right) = f\left( c \right)\) và \(\mathop {\lim }\limits_{x \to {d^ + }} f\left( x \right) = f\left( d \right)\).
\(\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right) = f\left( c \right)\) và \(\mathop {\lim }\limits_{x \to {d^ - }} f\left( x \right) = f\left( d \right)\).
\(\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right) = f\left( c \right)\) và \(\mathop {\lim }\limits_{x \to {d^ - }} f\left( x \right) = f\left( d \right)\).
\(\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right) = f\left( c \right)\) và \(\mathop {\lim }\limits_{x \to {d^ + }} f\left( x \right) = f\left( d \right)\).
Giới hạn \(\lim \frac{{4n + 2}}{{n - 1}}\) bằng
\( - 2\).
2.
\( - 1\).
4.
Tìm các khoảng trên đó hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}\) liên tục.
\(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
\(\left( { - \infty ;2} \right)\).
\(\left[ { - 2; + \infty } \right)\).
\(\mathbb{R}\).
Dãy số nào sau đây có giới hạn bằng 0?
\({u_n} = {\pi ^n}\).
\({u_n} = {\left( {\frac{2}{5}} \right)^n}\).
\({u_n} = {\left( {\frac{{12}}{5}} \right)^n}\).
\({u_n} = \frac{{{n^5}}}{{2n + 3}}\).
Cho các dãy số \({u_n},{v_n}\) và \(\lim {u_n} = a;\lim {v_n} = b\). Tính \(\lim \left( {{u_n} - {v_n}} \right)\).
\({a^b}\).
\(a - b\).
\(a + b\).
\(a \cdot b\).
\(\lim \left( {\sqrt {n + 1} - \sqrt n } \right)\) bằng
\(0\).
\( - \infty \).
\( + \infty \).
\(1\).
\[\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + 3x - 4} \right)\] bằng
\(0\).
\(6\).
\(4\).
\(1\).
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{1 - 5x - {x^3}}}{{{x^3} - x + 1}}\) bằng
\( - 1\).
\(1\).
\( - \infty \).
\(0\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\left( {m;n} \right),a \in \left( {m;n} \right)\). Phát biểu nào sau đây đúng?
Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)\).
Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = f\left( a \right)\).
Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left( a \right)\).
Hàm số \(y = f\left( x \right)\) liên tục tại \(x = a\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right)\).
Tính giới hạn \(\mathop {\lim }\limits_{x \to 3} \frac{{3{x^2} - 10x + 3}}{{x - 3}}\).
\(3\).
\(1\).
\(8\).
\( + \infty \).
Tính giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {3{x^2} + 1} }}{x}\).
\( - \sqrt 3 \).
\( - 3\).
\(\sqrt 3 \).
\( + \infty \).
Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {10 - {x^2}} - 3}}{{1 - {x^2}}}\).
\(1\).
\(\frac{1}{6}\).
\(0\).
\( - \frac{1}{6}\).
Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?
\(f\left( x \right) = \sqrt {x - 1} \).
\(f\left( x \right) = \cot x\).
\(f\left( x \right) = \sin x\).
\(f\left( x \right) = \tan x\).
Tính giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt[3]{{{x^3} - {x^2} + 1}} - \sqrt {{x^2} + 3} } \right)\).
\(0\).
\( - \infty \).
\( + \infty \).
\(2\).
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{5x - {x^2}}}{{\sqrt {{x^4} + 4{x^2}} }}\;\;{\rm{khi}}\;x < 0\\m + \frac{{2x - 3}}{{x + 2}}\;\;{\rm{khi}}\;x \ge 0\end{array} \right.\) liên tục tại điểm \({x_0} = 0\).
A. \(m = - 1\).
B. \(m = 4\).
C. \(m = \frac{1}{2}\).
D. \(m = - 3\).
Tính tổng \(S = 1 + \frac{1}{2} + \frac{1}{4} + ... + {\left( {\frac{1}{2}} \right)^n} + ...\) bằng
\(S = 2\).
\(S = \frac{1}{2}\).
\(S = 3\).
\(S = \frac{1}{3}\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\). Hàm số đã cho liên tục tại \({x_0} = 1\) khi
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\).
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right)\).
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = 1\).
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right)\).
Cho \[\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 1,\mathop {\lim }\limits_{x \to 0} g\left( x \right) = 2\]. Tính \(L = \mathop {\lim }\limits_{x \to 0} \left[ {f\left( x \right) + g\left( x \right)} \right]\).
\(L = - 1\).
\(L = 3\).
\(L = 1\).
\(L = 0\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 3\) và công bội \(q = - \frac{2}{3}\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\), với \(n \ge 1\). Giá trị \(\lim {S_n}\) bằng
\(\frac{9}{5}\).
\(\frac{6}{5}\).
\( - \frac{6}{5}\).
\( - \frac{9}{5}\).
Giá trị \(\mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 3}}{{\sqrt {5{x^2} - 4x + 2} + x}}\) bằng
\(0\).
\(\frac{{ - 2}}{{\sqrt 5 - 1}}\).
\(\frac{2}{{\sqrt 5 }}\).
\(\frac{2}{{\sqrt 5 + 1}}\).
Biết \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{7x + 1}} - 1}}{x} = \frac{a}{b}\), trong đó \(a,b\) là các số nguyên dương và phân số \(\frac{a}{b}\) tối giản. Tính giá trị của biểu thức \(P = ab\).
\(\frac{7}{3}\).
\(\frac{3}{7}\).
\(21\).
\(10\).
Nếu \(\lim {u_n} = a\) và \(\lim {v_n} = - \infty \) thì \(\lim \frac{{{u_n}}}{{{v_n}}}\) bằng
\( - \infty \).
\(0\).
\( + \infty \).
\(a\).
Cho hàm số \(f\left( x \right) = \frac{{x - {x^2}}}{{\left| x \right|}}\). Khi đó \(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\) bằng
\( - \infty \).
\(1\).
\(0\).
\( - 1\).
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\lim \left( {4 + {u_n}} \right) = 3\). Giá trị của \(\lim {u_n}\) bằng
\(3\).
\(7\).
\(1\).
\( - 1\).
Cho \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + ax + 5} + x} \right) = 5\) thì giá trị của \(a\) là một nghiệm của phương trình nào trong các phương trình sau?
\({x^2} - 8x + 15 = 0\).
\({x^2} - 11x + 10 = 0\).
\({x^2} + 9x - 10 = 0\).
\({x^2} - 5x + 6 = 0\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 2}}\;{\rm{khi}}\;x < 2\\{x^2} - x - 1\;\;\;\;{\rm{khi}}\;x \ge 2\end{array} \right.\).
a) \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1\).
b) \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 1\).
c) Hàm số \(f\left( x \right)\) gián đoạn tại điểm \(x = 2\).
d) Hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {x + 4} - 2}}{x}\;\;\;\;{\rm{khi}}\;x > 0\\m{x^2} + 2m + \frac{1}{4}{\rm{khi}}\;x \le 0\end{array} \right.\), với \(m\) là tham số.
Tập xác định của hàm số \(f\left( x \right)\) là \(D = \mathbb{R}\).
\(f\left( 0 \right) = 2m + \frac{1}{4}\).
\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = 1\).
Hàm số \(f\left( x \right)\) liên tục tại \(x = 0\) khi \(m = \frac{1}{4}\).
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l} - \frac{x}{2}\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{khi}}\;x \le 1\\\frac{{{x^2} - 3x + 2}}{{{x^2} - 1}}\;\;\;{\rm{khi}}\;x > 1\end{array} \right.\). Khi đó
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 2\).
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \frac{1}{2}\).
Hàm số \(y = f\left( x \right) + \sin x\) không liên tục tại điểm \({x_0} = 0\).
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 1\).
Cho \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = - 2\). Khi đó
Giới hạn \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{f\left( x \right)}} = \infty \).
Giới hạn \(\mathop {\lim }\limits_{x \to 3} \frac{{f\left( x \right)}}{{x - 3}}\) tồn tại hữu hạn.
\[\mathop {\lim }\limits_{x \to 3} \frac{{f\left( x \right)}}{{{{\left( {x - 3} \right)}^2}}} = - \infty \].
Giới hạn \(\mathop {\lim }\limits_{x \to 3} \frac{{{{\left( {x - 3} \right)}^2}}}{{f\left( x \right)}} = 0\).
Một điểm dịch vụ trông giữ xe ô tô thu phí 30 nghìn đồng trong giờ đầu tiên và thu thêm 20 nghìn đồng cho mỗi giờ tiếp theo.
Hàm số mô tả số tiền phí theo thời gian trông giữ là \(f\left( x \right) = \left\{ \begin{array}{l}30\;\;\;\;\;\;\;\;\;\;{\rm{khi}}\;0 < x \le 1\\10 + 20x\;\;{\rm{khi}}\;x > 1\end{array} \right.\).
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 30\).
Một người gửi xe ô tô trong 2,5 giờ thì số tiền phải trả là 55 nghìn đồng.
Hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( {0; + \infty } \right)\).
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) với \({u_n} = \frac{{2{n^2} - 4n + 7}}{{8{n^2} + 3n + 10}}\), \({v_n} = \frac{{\sqrt {4{n^2} + 5} }}{{8n}}\).
\(\lim {u_n} = 7\).
\(\lim \left( {{v_n} - \frac{1}{4}} \right) = 0\).
\(\lim \left( {2{u_n} - 4{v_n}} \right) = 0\).
\(\lim \frac{{{u_n}}}{{2{v_n}}} = \frac{1}{2}\).
Cho hàm số \(f\left( x \right) = \frac{{{x^2} - 2x}}{{\left| {x - 2} \right|}}\).
\(f\left( x \right) = x,\forall x \in \mathbb{R}\).
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 2\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = - 3\).
Không tồn tại giới hạn của hàm số khi \(x \to 2\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + x + 1\;\;\;\;{\rm{khi}}\;x \le - 1\\x + 2\;\;\;\;\;\;\;\;\;\;{\rm{khi}}\; - 1 < x < 1\\2x + 3\;\;\;\;\;\;\;\;{\rm{khi}}\;x \ge 1\end{array} \right.\).
a) Hàm số \(y = f\left( x \right)\)liên tục tại điểm \(x = - 2\).
b) Hàm số \(y = f\left( x \right)\) không liên tục tại điểm \(x = 0\).
c) Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = - 1\).
d) Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = 1\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 4}}{{x - 2}}\;\;\;\;\;\;{\rm{khi}}\;x > 2\\ax + 2024\;{\rm{khi}}\;x \le 2\end{array} \right.\).
\(f\left( 2 \right) = 0\).
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 4\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = - 4\).
\(a = - 1010\) thì tồn tại \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\).
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \frac{{2{n^2} - n + 1}}{{a{n^2} + n + 2}}\) và dãy số \(\left( {{v_n}} \right)\) biết \({v_n} = 3 - \frac{5}{{{2^n}}}\). Khi đó:
\(\lim {v_n} = - 2\).
Với \(a = 1\) thì \(\lim {u_n} = 2\).
Biết \(\lim {u_n} = 1\) và \(\lim {v_n} = b\) thì \(a \cdot b = 6\).
Không có giá trị nào của \(a\) để dãy số \(\left( {{u_n}} \right)\) có giới hạn vô cực.
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{9 - {x^2}}}{{x - 3}}\;\;{\rm{khi}}\;x < 3\\1 - x\;\;\;\;\;{\rm{khi}}\;x \ge 3\end{array} \right.\). Biết \(\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = a,\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = b\). Tính \({a^2} + {b^2}\).
Cho hai số thực \(a,b\) thỏa mãn \(\mathop {\lim }\limits_{x \to 2} \frac{{a{x^2} + bx - 2}}{{x - 2}} = 5\). Tính giá trị biểu thức \(S = a + 2b\).
Cho \(f\left( x \right)\) là đa thức thỏa mãn \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 20}}{{x - 2}} = 10\). Tính \(T = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{6f\left( x \right) + 5}} - 5}}{{{x^2} + x - 6}}\) (kết quả làm tròn đến hàng phần mười).
Giới hạn \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {{x^2} + 5} - 3}}{{x - 2}} = \frac{a}{b}\) (\(\frac{a}{b}\) là phân số tối giản). Tính \(a + b\).
Biết \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{1 + {x^2}}} - 1}}{{{x^2}}} = \frac{a}{b}\) (\(\frac{a}{b}\) là phân số tối giản \(a \in \mathbb{Z},b \in {\mathbb{N}^*}\)). Tính giá trị của biểu thức \(S = {a^2} + b.\)
Một đơn vị sản xuất ước tính rằng chi phí (đơn vị: triệu đồng) để sản xuất \(x\) đơn vị sản phẩm là \(C\left( x \right) = 100x\left( {\sqrt {9{x^2} + 18x + 12} - 3x} \right)\). Tìm hàm số \(f\left( x \right)\) biểu thị chi phí trung bình để sản xuất một đơn vị sản phẩm. Tính \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
Biết \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {4{x^2} + 1} - x}}{{5x}} = \frac{a}{b}\) trong đó \(a \in \mathbb{Z},b \in {\mathbb{N}^*}\) và phân số \(\frac{a}{b}\) tối giản. Tính giá trị biểu thức \(P = a + b\).
Cho \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = - 2\). Tính \(\mathop {\lim }\limits_{x \to 3} \left[ {f\left( x \right) + 4x - 1} \right]\).
Cho phí (đơn vị: triệu đồng) để sản xuất \(x\) sản phẩm của một công ty được xác định bởi hàm số \(C\left( x \right) = 2x + 55\). Gọi \(\overline C \left( x \right)\) là chi phí trung bình để sản xuất một sản phẩm. Khi số lượng sản phẩm sản xuất được càng lớn thì chi phí trung bình để sản xuất một sản phẩm càng gần với số tiền nào (đơn vị triệu đồng)?
Để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{2{x^2} - 3x + 1}}{{2\left( {x - 1} \right)}}\;{\rm{khi}}\;x \ne 1\\m\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{khi}}\;x = 1\end{array} \right.\) liên tục tại \(x = 1\) thì giá trị \(m\) bằng bao nhiêu?
Tìm giới hạn của các dãy số sau
(a) \(\lim \frac{{{n^2} + 5n}}{{3{n^2} - 2n + 1}}\);
(b) \(\lim \frac{{{3^n} - 2 \cdot {4^n}}}{{5 \cdot {4^n} + {3^n}}}\).
Tìm giới hạn của các hàm số sau:
(a) \(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + x - 2}}{{x + 2}}\);
(b) \[\mathop {\lim }\limits_{x \to 7} \frac{{\sqrt {x - 3} - 2}}{{{x^2} - 49}}\];
(c) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2\sqrt {5 - x} + \sqrt {7 - 3x} }}{{3{x^2} + 2x - 5}}.\)
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{1 - \sqrt {2x - 3} }}{{2 - x}}\;\;{\rm{khi}}\;x \ne 2\\1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{khi}}\;x = 2\end{array} \right.\) tại điểm \({x_0} = 2\).
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^3} + x + 1{\rm{ khi }}x \ge 1\\2x + 4{\rm{ khi }}x < 1\end{array} \right.\) trên tập xác định của nó.
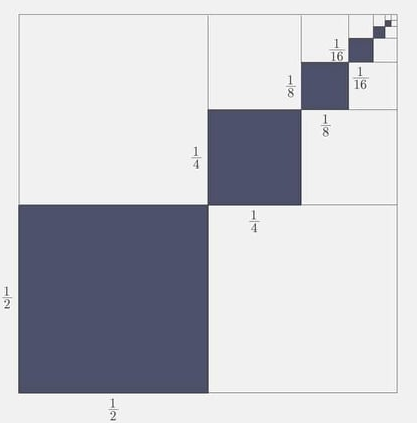
Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng 1. Nó tô màu xám các hình vuông nhỏ được đánh số lần lượt là 1, 2, 3, 4, …n,… trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó. Giả sử quy trình tô màu của chuột Mickey có thể tiến ra vô hạn (như hình vẽ dưới đây). Tính tổng diện tích mà chuột Mickey phải tô màu.