Đề kiểm tra Phương trình lượng giác cơ bản (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Nghiệm của phương trình \[\cos x = - \,\;\frac{1}{2}\] là
\(x = \pm \frac{{2\pi }}{3} + k2\pi \).
\(x = \pm \frac{\pi }{6} + k\pi \).
\(x = \pm \frac{\pi }{3} + k2\pi \).
\(x = \pm \frac{\pi }{6} + k2\pi \).
Phương trình \(\cos x = - \frac{{\sqrt 3 }}{2}\) có tập nghiệm là
\[\left\{ {x = \pm \frac{\pi }{6} + k\pi ; k \in \mathbb{Z}} \right\}\].
\[\left\{ {x = \pm \frac{{5\pi }}{6} + k2\pi ; k \in \mathbb{Z}} \right\}\].
\[\left\{ {x = \pm \frac{\pi }{3} + k\pi ; k \in \mathbb{Z}} \right\}\].
\[\left\{ {x = \pm \frac{\pi }{3} + k2\pi ; k \in \mathbb{Z}} \right\}\].
Tập nghiệm của phương trình \(\tan x + 1 = 0\) là
\(S = \left\{ { - \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ {\frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ { - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ {\frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}} \right\}\).
Tìm tất cả các giá trị của tham số \(m\) để phương trình \(\sin \,x - m = 1\) có nghiệm.
\(m \ge 1\).
\(m \le 0\).
\( - 2 \le m \le 0\).
\(0 \le m \le 1\).
Giải phương trình 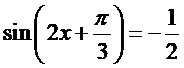
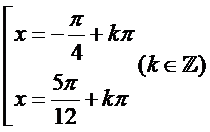 .
.
B. 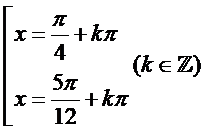 .
.
C. 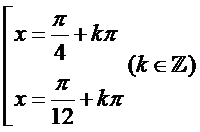 .
.
D. 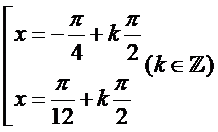 .
.
Với \(n = 5\), phương trình \(\sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = \sin x\) có nghiệm là
\(x = \frac{\pi }{2} + k\pi \).
\(x = \frac{\pi }{4} + k\pi \).
\(x = \frac{\pi }{2} + k2\pi \).
\(x = \frac{\pi }{4} + k\frac{\pi }{2}\).
Giải phương trình \(\cot \left( {2x - {{20}^0}} \right) = \frac{{\sqrt 3 }}{3}\)ta được
\(x = {40^0} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)\).
\(x = {40^0} + k\pi \left( {k \in \mathbb{Z}} \right)\).
\(x = {40^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\).
\(x = {40^0} + k{90^0}\left( {k \in \mathbb{Z}} \right)\).
Phương trình \(m.\cos x - 1 = 0\) có nghiệm khi \(m\) thỏa mãn điều kiện
\[\left\{ \begin{array}{l}m \ge - 1\\m \le 1\end{array} \right.\].
\[\left[ \begin{array}{l}m \le - 1\\m \ge 1\end{array} \right.\].
\[m \ge - 1\]
\[m \ge 1\].
Tìm tất cả các giá trị thực của tham số m để phương trình \[{\cos ^2}(\frac{x}{2} - \frac{\pi }{2}) = m\] có nghiệm.
\( - 1 \le m \le 1\)
\(m \le 1\).
\(m \ge 0\).
\(0 \le m \le 1\).
Nghiệm của phương trình \[\cos x = - \frac{1}{2}\] là
\[x = \pm \frac{{2\pi }}{3} + k2\pi \].
\[x = \pm \frac{\pi }{6} + k\pi \].
\[x = \pm \frac{\pi }{3} + k2\pi \].
\[x = \pm \frac{\pi }{6} + k2\pi \].
Phương trình \(\tan 3x = \tan x\) có nghiệm là
\(x = k\pi \).
\(x = k2\pi \).
\(x = k\frac{\pi }{2}\).
\(x = \frac{\pi }{2} + k\pi \).
Tìm \(m\) để phương trình \(\cos x - 2m + 1 = 0\) có nghiệm.
\(m > - \frac{1}{2}\).
\(0 < m < 1\).
\(0 \le m \le 1\).
\(m \ge - \frac{1}{2}\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình lượng giác \(2\cos x = \sqrt 3 \), khi đó:
a) Phương trình có nghiệm \(x = \pm \frac{\pi }{3} + k2\pi (k \in \mathbb{Z})\)
b) Trong đoạn \(\left[ {0;\frac{{5\pi }}{2}} \right]\) phương trình có 4 nghiệm
c) Tổng các nghiệm của phương trình trong đoạn \(\left[ {0;\frac{{5\pi }}{2}} \right]\) bằng \(\frac{{25\pi }}{6}\)
d) Trong đoạn \(\left[ {0;\frac{{5\pi }}{2}} \right]\) phương trình có nghiệm lớn nhất bằng \(\frac{{13\pi }}{6}\)
Cho phương trình lượng giác \(3 - \sqrt 3 \tan \left( {2x - \frac{\pi }{3}} \right) = 0\) , khi đó:
a) Phương trình có nghiệm \(x = \frac{\pi }{6} + \frac{{k\pi }}{2},k \in \mathbb{Z}\).
b) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{3}\)
c) Khi \(\frac{{ - \pi }}{4} < x < \frac{{2\pi }}{3}\) thì phương trình có ba nghiệm
d) Tổng các nghiệm của phương trình trong khoảng \(\left( {\frac{{ - \pi }}{4};\frac{{2\pi }}{3}} \right)\) bằng \(\frac{\pi }{6}\)
Cho phương trình lượng giác \(\sin x = - \frac{1}{2}\), khi đó:
a) Phương trình tương đương \(\sin x = \sin \left( {\frac{\pi }{6}} \right)\)
b) Phương trình có nghiệm là: \(x = - \frac{\pi }{6} + k2\pi ;x = \frac{{7\pi }}{6} + k2\pi (k \in \mathbb{Z})\).
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{3}\)
d) Số nghiệm của phương trình trong khoảng \(\left( { - \pi ;\pi } \right)\) là ba nghiệm
Một vật dao động xung quanh vị trí cân bằng theo phương trình \(x = 1,5\cos \left( {\frac{{t\pi }}{4}} \right)\); trong đó \(t\) là thời gian được tính bằng giây và quãng đường \(h = |x|\) được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng. Khi đó:
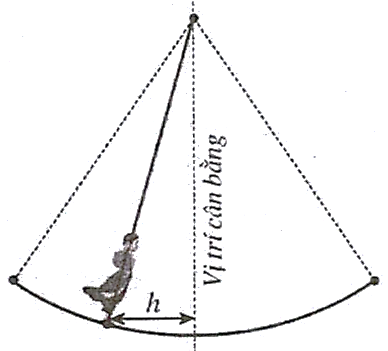
a) Vật ở xa vị trí cân bằng nhất nghĩa là \(h = 1,5\;m\).
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất
c) Khi vật ở vị trí cân bằng thì \(\cos \left( {\frac{{t\pi }}{4}} \right) = 0\)
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần?
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm nghiệm phương trình lượng giác:
Tìm nghiệm phương trình lượng giác: \(\tan \left( {2x - \frac{\pi }{6}} \right) = \frac{{\sqrt 3 }}{3}\)
Tìm nghiệm phương trình lượng giác: \(\sqrt 3 \tan \frac{{\pi x}}{2} = 3\).
Tìm nghiệm phương trình lượng giác\(\sin \left( {2x - \frac{1}{3}} \right) + \sin x = 0\)
Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình
\(x = 2{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\)
Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Trong Hình 9, khi được kéo ra khơi vị trí cân bằng ờ điểm \(O\) và buông tay, lực đàn hồi của lò xo khiến vật \(A\) gắn ở đầu của lò xo dao động quanh \(O\). Toạ độ \(s\left( {{\rm{\;cm}}} \right)\) của \(A\) trên trục \(Ox\) vào thời điểm \(t\) (giây) sau khi buông tay được xác định bởi công thức \(s = 10{\rm{sin}}\left( {10t + \frac{\pi }{2}} \right)\). Vào các thời điểm nào thì \(s = - 5\sqrt 3 {\rm{\;cm}}\)?