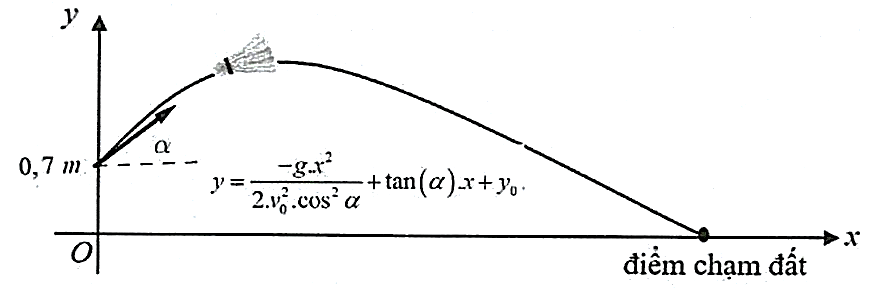Đề kiểm tra Phương trình lượng giác cơ bản (có lời giải) - Đề 1

Nghiệm của phương trình lượng giác \(\sin x = 5\) là

Tính \(\alpha \) biết \(\cos \alpha = 1\):

Giải phương trình \(\sqrt {\rm{3}} \tan 2x - 3 = 0\).

Phương trình \[\tan x = \tan \varphi \], \[\left( {\varphi \in \mathbb{R}} \right)\] có nghiệm là

Tất cả các nghiệm của phương trình \(\cot x = \cot \alpha \)là

Mệnh đề nào sau đây đúng với mọi số nguyên \(k\)?

Tìm tất cả các giá trị thực của than số m để phương trình sin x - m = 2 có nghiệm?              

Phương trình \[\sin 2x = - \frac{{\sqrt 2 }}{2}\] có bao nhiêu nghiệm thuộc khoảng \[\left( {0;\,\pi } \right)?\]              

Phương trình \(\sin 2x\, = \, - \frac{1}{2}\) có hai họ nghiệm có dạng \(x = \alpha  + k\pi \) và \(x = \,\beta  + k\pi \), \(k \in \mathbb{Z}\)\(\left( { - \frac{\pi }{4} < \alpha  < 0 < \beta  < \frac{{3\pi }}{4}} \right)\). Khi đó: Tính \({\beta ^2} - {\alpha ^2}\)?

Phương trình \(\tan x\, = \sqrt 3 \)có bao nhiêu nghiệm trong khoảng \(\left( {0\,;\,\pi } \right)\)?              

Tìm số nghiệm của phương trình \[\tan x = \tan \frac{{3\pi }}{8}\] trên \(\left( {\frac{\pi }{4};2\pi } \right)\).              

Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho phương trình lượng giác \(\sin 2x = - \frac{1}{2}\) (*). Khi đó:

a) Phương trình (*) tương đương \(\sin 2x = \sin \frac{\pi }{6}\)

b) Trong khoảng \(\left( {0;\pi } \right)\) phương trình có 3 nghiệm

c) Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{3\pi }}{2}\)

d) Trong khoảng \(\left( {0;\pi } \right)\) phương trình có nghiệm lớn nhất bằng \(\frac{{11\pi }}{{12}}\)

Cho phương trình \(\sin \left( {2x - \frac{\pi }{4}} \right) = \sin \left( {x + \frac{{3\pi }}{4}} \right)\) (*), vậy:

a) Phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{x = \pi + k2\pi }\\{x = \frac{\pi }{6} + k\frac{{2\pi }}{3}}\end{array}(k \in \mathbb{Z}){\rm{.}}} \right.\)

b) Trong khoảng \((0;\pi )\) phương trình có 2 nghiệm

c) Tổng các nghiệm của phương trình trong khoảng \((0;\pi )\) bằng \(\frac{{7\pi }}{6}\)

d) Trong khoảng \((0;\pi )\) phương trình có nghiệm lớn nhất bằng \(\frac{{5\pi }}{6}\)

Cho phương trình lượng giác \(2\sin x = \sqrt 2 \), khi đó:

a) Phương trình tương đương \(\sin x = \sin \frac{\pi }{4}\)

b) Phương trình có nghiệm là: \(x = \frac{\pi }{3} + k2\pi ;x = \frac{{3\pi }}{4} + k2\pi (k \in \mathbb{Z})\).

c) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{\pi }{4}\)

d) Số nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là hai nghiệm

Cho hai đồ thị hàm số \(y = \sin \left( {x + \frac{\pi }{4}} \right)\) và \(y = \sin x\), khi đó:

a) Phương trình hoành độ giao điểm của hai đồ thị hàm số:\(\sin \left( {x + \frac{\pi }{4}} \right) = \sin x\)

b) Hoành độ giao điểm của hai đồ thị là \(x = \frac{{3\pi }}{8} + k\pi (k \in \mathbb{Z})\)

c) Khi \(x \in [0;2\pi ]\) thì hai đồ thị hàm số cắt nhau tại ba điểm

d) Khi \(x \in [0;2\pi ]\) thì toạ độ giao điểm của hai đồ thị hàm số là: \(\left( {\frac{{5\pi }}{8};\sin \frac{{5\pi }}{8}} \right),\left( {\frac{{7\pi }}{8};\sin \frac{{7\pi }}{8}} \right)\).

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Tìm nghiệm phương trình lượng giác: $\cos \left(x+{30}^{°}\right)+1=0$

Tìm nghiệm phương trình lượng giác\(\cot 3x = \cot (\pi - x)\);

Tìm \(m\) để các phương trình lượng giác sau có nghiệm: \(2\sin 3x = m - 1\).

Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(\sin x - m = 1\) có nghiệm.

Khi một tia sáng truyền từ ông khí vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26. Góc tới \(i\) liên hệ với góc khúc xạ \(r\) bởi Định luật khúc xạ ánh sáng \(\frac{{{\rm{sin}}i}}{{{\rm{sin}}r}} = \frac{{{n_2}}}{{{n_1}}}{\rm{.\;}}\)

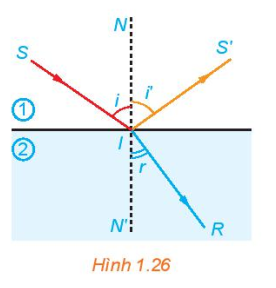
Ở đây, \({n_1}\) và \({n_2}\) tương ứng là chiết suất của môi trường 1 (không khí) và môi trường 2 (nước). Cho biết góc tới \(i = {50^ \circ }\), hãy tính góc khúc xạ, biết rằng chiết suất của không khí bằng 1 còn chiết suất của nước là 1,33.

Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên.

Trong mặt phẳng toạ độ \(Oxy\), chọn điểm có tọa độ \(\left( {O;{y_0}} \right)\) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: \(y = \frac{{ - g \cdot {x^2}}}{{2 \cdot v_0^2 \cdot {{\cos }^2}\alpha }} + \tan (\alpha ) \cdot x + {y_0}\); trong đó:

g là gia tốc trọng trường (thường được chọn là \(9,8\;m/{s^2}\) );

\(\alpha \) là góc phát cầu (so với phương ngang của mặt đất);

\({v_0}\) là vận tốc ban đầu của cầu;

\({y_0}\) là khoảng cách từ vị trí phát cầu đến mặt đất.

Đây là một hàm số bậc hai nên quỹ đạo chuyển động của cầu lông là một parabol.

Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là \(6,68\;m\). Quan sát hình bên dưới, hỏi người chơi đã phát cầu góc khoảng bao nhiêu độ so với mặt đất? ( biết cầu rời mặt vợt ở độ cao \(0,7\;m\) so với mặt đất và vận tốc xuất phát của cầu là \(8\;m/s\), bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng phẳng đứng).