Đề kiểm tra Phương trình lượng giác cơ bản (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Phương trình \(\sin 2x = \frac{1}{2}\) có tập nghiệm là
\(S = \left\{ {\frac{\pi }{{12}} + k\pi ,\,\,\frac{{5\pi }}{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ {\frac{\pi }{6} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\).
\(C = \left\{ {\frac{\pi }{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
\(S = \left\{ {\frac{\pi }{{18}} + k\frac{\pi }{2},\,\,k \in \mathbb{Z}} \right\}\).
Nghiệm của phương trình \(\sin 2x = 1\) là
\(x = \frac{\pi }{4} + k\pi \).
\(x = \frac{\pi }{4} + k2\pi \).
\(x = \frac{{k\pi }}{2}\).
\(x = \frac{\pi }{2} + k2\pi \).
Phương trình \(2\cos x - 1 = 0\) có một nghiệm là
\(x = \frac{\pi }{4}\).
\(x = \frac{\pi }{6}\).
\(x = \frac{\pi }{3}\).
\(x = \frac{\pi }{2}\).
Phương trình nào sau đây có nghiệm?
\[\cos x = - \frac{3}{2}\].
\(\sin x = \sqrt 2 \).
\(\tan x = 3\).
\[{\cos ^2}x - 3 = 0\].
Giải phương trình \(\tan \left( {2x} \right) = \tan \,80^\circ \). Kết quả thu được là
\(x = 80^\circ + k180^\circ \).
\(x = 40^\circ + k90^\circ \).
\(x = 40^\circ + k45^\circ \).
\(x = 40^\circ + k180^\circ \).
Phương trình \(\cot \left( {x + 45^\circ } \right) = \frac{{\sqrt 3 }}{3}\) có nghiệm là (với \(k \in \mathbb{Z}\))
\(15^\circ + k180^\circ \).
\(30^\circ + k180^\circ \).
\(45^\circ + k180^\circ \).
\(60^\circ + k180^\circ \).
Phương trình \(\cos x - m = 0\)vô nghiệm khi giá trị tham số \(m\)thỏa mãn.
\(\left[ \begin{array}{l}m < - 1\\m > 1\end{array} \right.\).
\( - 1 \le m \le 1\).
\(m > 1\).
\(m < - 1\).
Tập nghiệm của phương trình: \(2\cos x + \sqrt 3 = 0\) là:
\[\left\{ { \pm \frac{{5\pi }}{6} + k2\pi |k \in \mathbb{Z}} \right\}\].
\[\left\{ { \pm \frac{\pi }{6} + k2\pi |k \in \mathbb{Z}} \right\}\].
\[\left\{ { \pm \frac{\pi }{6} + k\pi |k \in \mathbb{Z}} \right\}\].
\[\left\{ { \pm \frac{{5\pi }}{6} + k\pi |k \in \mathbb{Z}} \right\}\].
Nghiệm của phương trình \(\sqrt 3 + 3\tan x = 0\) là
\(x = \frac{\pi }{3} + k\pi \).
\(x = \frac{\pi }{2} + k2\pi \).
\(x = - \frac{\pi }{6} + k\pi \).
\(x = \frac{\pi }{2} + k\pi \).
Chọn đáp án sai trong các câu sau:
\(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \).
\(\cot x = - 1 \Leftrightarrow x = - \frac{\pi }{4} + k\pi \).
\(\cos x = - 1 \Leftrightarrow x = \pi + k\pi \).
\(\tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \).
Giải phương trình \(\cot 2x = \cot 20^\circ \).
\(x = 10^\circ + k90^\circ ,k \in \mathbb{Z}\).
\(x = 10^\circ + k180^\circ ,k \in \mathbb{Z}\).
\(x = 20^\circ + k90^\circ ,k \in \mathbb{Z}\).
\(x = 20^\circ + k180^\circ ,k \in \mathbb{Z}\).
Phương trình \(\cot 3x = \cot x\) có các nghiệm là:
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\).
\(x = k\pi ,k \in \mathbb{Z}\).
\(x = \frac{{k\pi }}{3},k \in \mathbb{Z}\).
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình lượng giác (*). Khi đó:
a) Phương trình (*) có nghiệm
b) Phương trình có nghiệm âm lớn nhất bằng \( - 30^\circ \)
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - 180^\circ ;90^\circ } \right)\) bằng \(180^\circ \)
d) Trong khoảng \(\left( { - 180^\circ ;90^\circ } \right)\) phương trình có nghiệm lớn nhất bằng \(60^\circ \)
Cho phương trình lượng giác \(\cot 3x = - \frac{1}{{\sqrt 3 }}\) (*). Khi đó
a) Phương trình (*) tương đương \(\cot 3x = \cot \left( {\frac{{ - \pi }}{6}} \right)\)
b) Phương trình (*) có nghiệm \(x = \frac{\pi }{9} + k\frac{\pi }{3}(k \in \mathbb{Z})\)
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};0} \right)\) bằng \(\frac{{ - 5\pi }}{9}\)
d) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{{2\pi }}{9}\)
Cho phương trình lượng giác \(\sin \left( {3x + \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{2}\)
a) Phương trình có nghiệm \[\left[ {\begin{array}{*{20}{l}}{x = - \frac{\pi }{9} + k\frac{{2\pi }}{3}}\\{x = \frac{\pi }{3} + k\frac{{2\pi }}{3}}\end{array}(k \in \mathbb{Z})} \right.\]
b) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{{2\pi }}{9}\)
c) Trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) phương trình đã cho có 3 nghiệm
d) Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\frac{\pi }{2}} \right)\) bằng \(\frac{{7\pi }}{9}\)
Cho phương trình lượng giác , vậy:
a) Phương trình tương đương với
b) Đồ thị hàm số cắt trục hoành tại điểm gốc tọa độ
c) Phương trình có nghiệm là:
d) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) phương trình đã cho có một nghiệm
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm nghiệm phương trình lượng giác \(\sin x\sin \left( {x - \frac{\pi }{{18}}} \right) = 0\)
Tìm nghiệm phương trình lượng giác \(2\cos 2x - 8\cos x + 7 = \frac{1}{{\cos x}}\).
Tìm nghiệm phương trình lượng giác \(\cos \left( {x - \frac{{3\pi }}{4}} \right) + \cos \left( {x + \frac{\pi }{3}} \right) = 0\);
Tìm nghiệm phương trình lượng giác \(\sin \left( {x - \frac{{2\pi }}{3}} \right) - \cos 2x = 0\);
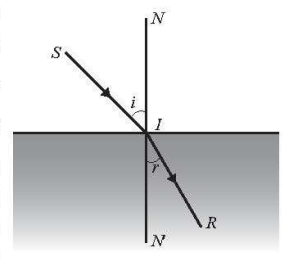
Theo Định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số \(\frac{{{\rm{sin}}i}}{{{\rm{sin}}r}}\), với \(i\) là góc tới và \(r\) là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là \({45^ \circ }\) thì góc khúc xạ bằng \({30^ \circ }\). Khi góc tới là \({60^ \circ }\) thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.
Một vệ tinh bay quanh Trái Đất theo một quỹ đạo hình Elip (như hình vẽ):
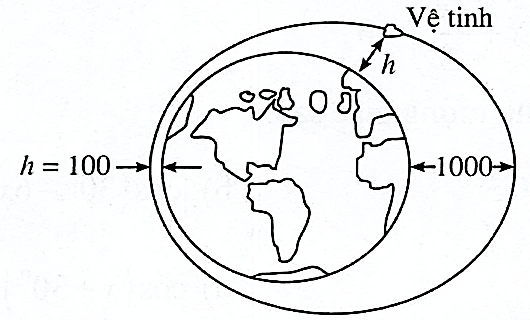
Độ cao \(h\) (tính bằng kilômet) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức \(h = 550 + 450 \cdot \cos \frac{\pi }{{50}}t\). Trong đó \(t\) là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người ta cần thực hiện một thí nghiệm khoa học khi vệ tinh cách mặt đất \(250\;km\). Trong khoảng 60 phút đầu tiên kể từ lúc vệ tinh bay vào quỹ đạo, hãy tìm thời điểm để có thể thực hiện thí nghiệm đó ?







