Đề kiểm tra Mẫu số liệu ghép nhóm (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Số học sinh có chiều cao từ 156 cm trở lên là
37
77
12
25
Có bao nhiêu xe không bị phạt tiền hoặc bị phạt tiền dưới 300.000 đồng?
105
97
27
70
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:

Mốt của mẫu số liệu ghép nhóm trên gần bằng giá trị nào sau đây?
\[19,4\].
\[18,4\].
\[20,4\].
\[21,4\].
Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:

Mốt của mẫu số liệu ghép nhóm trên gần bằng giá trị nào sau đây?
\[8,1\].
\[8,2\].
\[8,3\].
\[8,4\].
Mỗi nhóm số liệu ghép nhóm là tập hợp gồm:
các giá trị của số liệu được ghép nhóm theo nhiều tiêu chí xác định.
các giá trị của số liệu được ghép nhóm theo hai tiêu chí xác định.
các giá trị của số liệu được ghép nhóm theo một tiêu chí xác định.
các giá trị của số liệu được ghép nhóm theo ba tiêu chí xác định.
Mẫu số liệu ghép nhóm được dùng khi nào?
khi ta có thể thu thập được số liệu chính xác hoặc do yêu cầu của bài toán mà ta phải biểu diễn mẫu số liệu dưới dạng ghép nhóm để thuận lợi cho việc tổ chức, đọc và phân tích số liệu.
khi ta không thể thu thập được số liệu chính xác hoặc do yêu cầu của bài toán mà ta phải biểu diễn mẫu số liệu dưới dạng ghép nhóm để thuận lợi cho việc phân tích số liệu.
khi ta không thể thu thập được số liệu chính xác hoặc do yêu cầu của bài toán mà ta phải biểu diễn mẫu số liệu dưới dạng ghép nhóm để thuận lợi cho việc tổ chức, đọc và phân tích số liệu.
Cả ba câu trên đểu sai.
Cho mẫu số liệu ghép nhóm về số tiền mà sinh viên chi cho thanh toán cước điện thoại trong tháng

Có bao nhiêu sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng
5
23
12
17
Điều tra về chiều cao của học sinh khối lớp 11, ta được mẫu số liệu sau: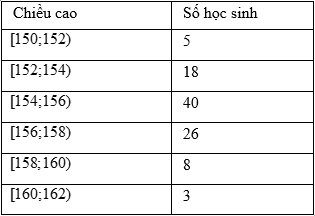
Mẫu số liệu ghép nhóm đã cho có bao nhiêu nhóm?
5
6
7
12
Cho bảng khảo sát về cân nặng học sinh trong lớp:

Khoảng cân nặng mà số học sinh chiếm nhiều nhất là:
\([60;65)\)
\([55;60)\)
\([50;55)\)
\([60;65)\)
Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:
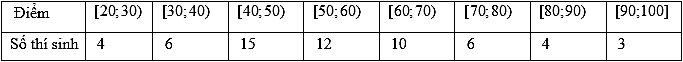
Có bao nhiêu học sinh thi trượt môn Toán? Biết rằng thí sinh đạt từ 50 điểm trở nên thì tính là đỗ.
24
25
26
27
Để đánh giá kết quả của một đề tài sau khi áp dụng vào thực tiễn dạy học người ta thực nghiệm bằng cách ra đề kiểm tra một tiết cho ba lớp 12A, 12B và 12C. Kết quả điểm của học sinh ba lớp như sau:
Lớp nào có tỉ lệ học sinh đạt điểm giỏi cao nhất?
Lớp 12A
Lớp 12B
Lớp 12C
Cả 3 lớp có tỉ lệ học sinh đạt điểm giỏi bằng nhau
Một trường trung học cơ sở chọn 36 học sinh nam của khối 9 để đo chiều cao của các bạn học sinh đó và thu được mẫu số liệu theo bảng sau (đơn vị là centimet)
Từ mẫu số liệu không ghép nhóm trên, hãy ghép các số liệu thành 5 nhóm theo các nửa khoảng có độ dài bằng nhau. Các nhóm đó là:
\([160;163);[163;165);[165;170);[170;172);[172;175)\).
\([160;165);[165;168);[168;170);[170;172);[172;175)\).
\([160;163);[163;166);[166;169);[169;172);[172;175)\).
\([160;162);[162;166);[166;168);[168;170);[172;175)\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Số lượng người đi xem một bộ phim mới theo độ tuổi trong một rạp chiếu phim (sau \(1\;h\) đầu công chiếu) được ghi lại theo bảng phân phối ghép nhóm sau:
Độ tuổi | \([10;20)\) | \([20;30)\) | \([30;40)\) | \([40;50)\) | \([50;60)\) |
Số người | 6 | 12 | 16 | 7 | 2 |
a) Giá trị đại diện nhóm \([50;60)\)là \(55\)
b) Độ tuổi được dự báo là ít xem phim đó nhất là thuộc nhóm \([50;60)\)
c) Nhóm chứa mốt là nửa khoảng \([30;40)\).
d) Độ tuổi được dự báo là thích xem phim đó nhiều nhất là 31 tuổi.
Một mẫu số liệu được cho ở dạng bảng tần số ghép nhóm như sau:
Nhóm | \([0;5)\) | \([5;10)\) | \([10;15)\) | \([15;20)\) | \([20;25)\) |
Tần số | 11 | 31 | 45 | 21 | 12 |
a) Mẫu trên có: \(110\) số liệu
b) Mẫu trên chia thành 5 nhóm.
c) Tần số của nhóm \([0;5)\) bằng 11
d) Tần số của nhóm \([20;25)\) là cao nhất
Một mẫu số liệu được cho ở dạng bảng tần số ghép nhóm như sau:
Nhóm | \([0,5;2,5)\) | \([2,5;4,5)\) | \([4,5;6,5)\) | \([6,5;8,5)\) | \([8,5;10,5)\) |
Tần số | 4 | 7 | 16 | 8 | 5 |
a) Cỡ mẫu của mẫu số liệu là \(40\).
b) Nhóm \([0,5;2,5)\) có giá trị đại diện là 1,5
c) Nhóm \([4,5;6,5)\) có giá trị đại diện là 5,5
d) Nhóm \([8,5;10,5)\) có độ dài lớn nhất trong các nhóm còn lại
Thống kê số giờ tự học của học sinh tại một trường THPT trong một tuần, người ta ghi được kết quả sau (đơn vị: giờ).
\(\begin{array}{*{20}{l}}{14}&{12,5}&{15}&{16,5}&{17}&{14,5}&{13}&{15,5}&{16,5}&{17,5}\\{16,5}&{18,5}&{19}&{20}&{19,5}&{17}&{16,5}&{14}&{18}&{21}\\{15,5}&{13,5}&{12,5}&{14,5}&{17,5}&{19}&{19,5}&{20,5}&{20}&{17}\\{14,5}&{13}&{14,5}&{18}&{16}&{15}&{13}&{18,5}&{14,5}&{12,5}\end{array}\)
a) Tổng số giờ tự học của học sinh là: 829,5 giờ.
b) Tổng hợp kết quả tự học của học sinh vào bảng tần số ghép nhóm theo mẫu sau:
Giờ tự học | \([12,5;14,5)\) | \([14,5;16,5)\) | \([16,5;18,5)\) | \([18,5;20,5)\) | \([20,5;22,5)\) |
Số học sinh | 9 | 13 | 17 | 9 | 2 |
c) Thời gian trung bình học của mỗi học sinh dựa vào bảng tần số ghép nhóm tìm được ở ý b) là: \(16,78.\)
d) Khả năng tự học trong tuần cao nhất của học sinh là 16,28 giờ.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một kĩ thuật viên ghi lại cân nặng của 20 chi tiết máy ở bảng sau (đơn vị: gam):
5,63 | 5,58 | 5,42 | 5,58 | 5,56 | 5,54 | 5,55 | 5,40 | 5,60 | 5,56 |
5,46 | 5,51 | 5,58 | 5,48 | 5,61 | 5,50 | 5,54 | 5,64 | 5,43 | 5,63 |
a) Tính cân nặng trung bình của mỗi chi tiết máy.
b) Lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \([5,40;5,45)\) và ước lượng số trung bình của mẫu số liệu ghép nhóm trên.
Bảng sau thống kê số lượt chở khách mỗi ngày của một lái xe taxi trong 30 ngày.
15 | 13 | 7 | 5 | 18 | 13 | 11 | 9 | 10 | 8 | 14 | 11 | 16 | 10 | 9 |
13 | 11 | 12 | 13 | 15 | 12 | 13 | 6 | 8 | 17 | 13 | 6 | 18 | 12 | 13 |
a) Hãy tính số trung bình và mốt của mẫu số liệu trên.
b) Hãy lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \([4,5;7,5)\).
c) Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm đó.
Theo Tổ chức Y tế Thế giới (WHO), thiếu máu là tình trạng giảm lượng huyết sắc tố (Hb) dẫn tới sự thiếu cung cấp oxygen cho các mô trong cơ thể. Đối với nam giới trên 15 tuổi, chỉ số Hb (đơn vị tính là g/l) lớn hơn hoặc bằng 130 được xem là không bị thiếu máu, từ 110 đến dưới 130 là thiếu máu mức nhẹ, từ 80 đến dưới 110 là thiếu máu mức vừa, dưới 80 là mức nặng. Đo chỉ số Hb của một số học sinh nam lớp 12 cho kết quả như sau:
\(\begin{array}{l}132,135,137,131,129,125,140,147,138,137,128,112,\\127,129,125,98,139,138,139,141,140,105,136,133,\\137,138,108,133,136,141,144,134,136,137,142.\end{array}\)
Ghép nhóm cho mẫu số liệu này theo mức độ thiếu máu.
Cân nặng của 28 học sinh nam lớp 11 được cho như sau:
\(\begin{array}{*{20}{l}}{55,4}&{62,6}&{54,2}&{56,8}&{58,8}&{59,4}&{60,7}&{58}&{59,5}&{63,6}&{61,8}&{52,3}&{63,4}&{57,9}\end{array}\)\(\begin{array}{*{20}{l}}{49,7}&{45,1}&{56,2}&{63,2}&{46,1}&{49,6}&{59,1}&{55,3}&{55,8}&{45,5}&{46,8}&{54}&{49,2}&{52,6}\end{array}\)Hãy chia mẫu dữ liệu trên thành 5 nhóm, lập bảng tần số ghép nhóm và xác định giá trị đại diện cho mỗi nhóm.
Một cửa hàng đã thống kê số ba lô bán được mỗi ngày trong tháng 9 với kết quả cho như sau:
\(\begin{array}{*{20}{l}}{12}&{29}&{12}&{19}&{15}&{21}&{19}&{29}&{28}&{12}&{15}&{25}&{16}&{20}&{29}\\{21}&{12}&{24}&{14}&{10}&{12}&{10}&{23}&{27}&{28}&{18}&{16}&{10}&{20}&{21}\end{array}\)
Hãy chia mẫu số liệu trên thành 5 nhóm, lập bảng tần số ghép nhóm, hiệu chỉnh bảng tần số ghép nhóm và xác định giá trị đại diện cho mỗi nhóm.
Mẫu số liệu dưới đây ghi lại tốc độ của 42 ô tô khi đi qua một trạm đo tốc độ (đơn vị: \(km/h\) ):
\(\begin{array}{*{20}{c}}{47,5}&{49,5}&{46}&{51}&{52,5}&{45}&{61}\\{42}&{67}&{48}&{63}&{65}&{62,5}&{49,5}\\{43,5}&{41}&{57,5}&{63,5}&{56,5}&{53}&{48}\\{61,5}&{46}&{57}&{69}&{44,5}&{52}&{50}\\{45}&{55}&{47}&{60}&{67,5}&{62}&{58}\\{56}&{51,5}&{57,5}&{59}&{52}&{43}&{56}\end{array}\)
Lập bảng tần số ghép nhóm bao gồm cả tần số tích luỹ cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng:
\([40;45),[45;50),[50;55),[55;60),[60;65),[65;70).\)






