Đề kiểm tra giữa học kì 2 Toán lớp 7 CTST - Đề 02 có đáp án
18 câu hỏi
Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được
12,5 : 34,5;
29 : 65;
25 : 69;
1 : 3.
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
–6;
0;
–9;
–1.
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
–32;
32;
–2;
2.
Cho hình vẽ sau:
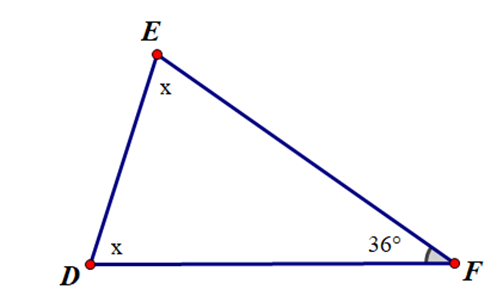
Số đo x là
18°;
72°;
36°;
Không xác định được.
Hai tam giác bằng nhau là
Hai tam giác có ba cặp cạnh tương ứng bằng nhau;
Hai tam giác có ba cặp góc tương ứng bằng nhau;
Hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau;
Hai tam giác có hai cạnh bằng nhau.
Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là
50°;
40°;
140°;
100°.
Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng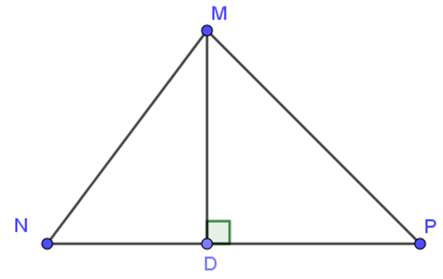
DN = DP;
MN = MP;
MD > MN;
MD < MP.
Điền vào chỗ trống sau: “Điểm … hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó”
thuộc;
cách đều;
nằm trên;
nằm trong.
Tìm số hữu tỉ x trong tỉ lệ thức sau:
\(\frac{5}{6}:x = 20:3\);
Tìm số hữu tỉ x trong tỉ lệ thức sau:
\(\frac{{9x - 1}}{9} = \frac{5}{3}\);
Tìm số hữu tỉ x trong tỉ lệ thức sau:
\(\frac{{x + 11}}{{14 - x}} = \frac{2}{3}\).
Tìm giá trị a, b thỏa mãn 3a = 4b và b – a = 5.
Cho \(\frac{a}{2} = \frac{b}{3};\,\,\frac{b}{5} = \frac{c}{4}\). Tìm a, b, c biết a + b + c = –74.
Một ô tô đi từ A lúc 8 giờ. Đến 9 giờ một ô tô khác cũng đi xe từ A. Xe thứ nhất đến B lúc 2 giờ chiều. Xe thứ hai đến B sớm hơn xe thứ nhất nửa giờ. Tính vận tốc mỗi xe biết rằng vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Chứng minh rằng ∆BME = ∆CNF.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN
ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H. Chứng minh ba điểm A, O, H thẳng hàng.
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh rằng \(\frac{{a - 2b}}{b} = \frac{{c - 2d}}{d}\).








