Đề kiểm tra Các số đặc trưng đo độ phân tán (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho phương sai của các số liệu bằng \(4\). Tìm độ lệch chuẩn.
\(4\).
\(2\).
\(16\).
\(8\).
Độ lệch chuẩn là
Căn bậc hai của phương sai.
Bình phương của phương sai.
Một nửa của phương sai.
Không phải các công thức trên.
Nếu đơn vị đo của số liệu là kg thì đơn vị của độ lệch chuẩn là
kg.
kg\(^2\).
Không có đơn vị.
\(\frac{{kg}}{2}\).
Tìm phát biểu đúng về phương sai của một mẫu số liệu.
Phương sai được sử dụng làm đại diện cho các số liệu của mẫu.
Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
Phương sai được tính bằng tổng số phần tử của một mẫu số liệu.
Phương sai là số liệu xuất hiện nhiều nhất (số liệu có tần số lớn nhất) trong bảng các số liệu thống kê.
Cho dãy số liệu thống kê: \(1\); \(2\); \(3\); \(4\); \(5\); \(6\); \(7\). Phương sai của các số liệu thống kê là
\(1\).
\(2\).
\(3\).
\(4\).
Cho dãy số liệu thống kê: \(1\); \(2\); \(3\); \(4\); \(5\); \(6\); \(7\). Khoảng biến thiên là
\(1\).
\(2\).
\(3\).
\(6\).
Số liệu thống kê \(100\) học sinh tham gia kì thi học sinh giỏi toán (thang điểm 20). Kết quả được thống kê trong bảng sau:
Tính độ lệch chuẩn của bảng số liệu thống kê.
\(2,01\).
\(1,89\).
\(1,98\).
\(1,99\).
Cho mẫu số liệu thống kê \[\left\{ {1;2;3;\,4;\,5;\,6;7;\,8;\,9} \right\}\].Tính (gần đúng) độ lệch chuẩn của mẫu số liệu trên?
\(2,45\).
\(2,58\).
\(6,67\).
\(6,0\).
Tính độ lệch chuẩn của bảng số liệu \[\left( I \right)\]. (Tính chính xác đến chữ số hàng phần trăm).
\[1,24\].
\[1,23\].
\[1,25\].
\[1,26\].
Theo kết quả thống kê điểm thi giữa kỳ 2 môn toán khối 11 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là \(s_x^2 = 0,573\). Độ lệch chuẩn của bảng thống kê đó bằng
\(0,812\).
\(0,757\).
\(0,936\).
\(0,657\).
Cho phương sai của các số liệu bằng \(4\). Tìm độ lệch chuẩn.
\(4\).
\(2\).
\(16\).
\(8\).
Cho mẫu số liệu \(\left\{ {10\,;\,7\,;\,8\,;\,5\,;\,4} \right\}\). Phương sai của mẫu là
\(2,39\).
\(2,14\).
\(4,56\).
\(5,7\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Kết quả kiểm tra môn Tiếng Anh (thang điểm 100) của hai lớp \(10\;A\) và \(10\;B\) được cho dưới bảng sau:
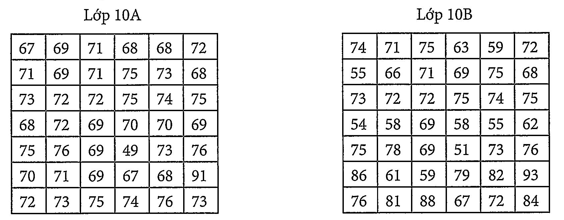
Khi đó:
a) Điểm trung bình Lớp 10A bằng 71,38
b) Phương sai Lớp 10B bằng 28,09
c) Độ lệch chuẩn Lớp 10A bằng 5,30
d) Lớp 10A học đồng đều hơn 10B.
Cho hai mẫu số liệu \(A\) và \(B\) được cho dưới dạng tần số như sau:
Mẫu A:
Giá trị | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Tân số | 1 | 2 | 3 | 3 | 2 | 4 | 2 | 4 | 1 | 3 | 4 | 2 | 1 | 1 |
Mẫu B:
Giá trị | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Tần số | 1 | 0 | 1 | 1 | 2 | 2 | 3 | 5 | 10 | 4 | 2 | 1 | 0 | 1 |
Khi đó:
a) Với mẫu A ta có: giá trị trung bình \(\overline {{x_A}} = 7,27\)
b) Với mẫu \(B\) ta có phương sai \(s_B^2 = 6,21\)
c) Với mẫu A ta có độ lệch chuẩn \({s_A} = 2,5\).
d) Mẫu \(A\) có độ phân tán cao hơn mẫu \(B\).
Thực hành việc đo chiều cao \((cm)\) của 40 học sinh nữ khối lớp 10 của một trường Trung học phổ thông, ta được kết quả như sau:
154 | 152 | 154 | 151 | 150 | 149 | 153 | 154 | 152 | 152 |
150 | 152 | 150 | 153 | 152 | 156 | 153 | 156 | 105 | 153 |
156 | 154 | 154 | 152 | 152 | 152 | 154 | 155 | 155 | 153 |
156 | 147 | 155 | 154 | 156 | 157 | 149 | 153 | 170 | 154 |
Khi đó:
a) Chiều cao trung bình: \(\bar x{ = _{152,27}}\;cm\).
b) 170 cm là chiều cao lớn nhất
c) Phương sai: \({s^2} = 65,32\);
d) Độ lệch chuẩn: \(s = 8,08\).
Một cơ sở chăn nuôi gia câm tiến hành nuôi thử nghiệm giống gà đẻ trứng mới. Khi gà đã cho trứng họ tiến hành khảo sát với 20 quả được cân nặng (gam) như sau:
40 | 42 | 36 | 38 | 40 | 42 | 29 | 48 | 43 | 43 |
41 | 41 | 39 | 44 | 45 | 41 | 40 | 39 | 42 | 41 |
Khi đó:
a) Giá trị nhỏ nhất của mẫu là 29
b) Giá trị lớn nhất của mẫu là \(48\)
c) Khoảng tứ phân vị: \({\Delta _Q} = 2\).
d) Các giá trị bất thường là 29 và 48.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Sản lượng lúa (đơn vị: tạ) của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng tần số sau đây:
Sản lượng | 20 | 21 | 22 | 23 | 24 |
Tần số | 5 | 8 | 11 | 10 | 6 |
Tìm độ lệch chuẩn của mẫu số liệu đã cho.
Mẫu số liệu sau ghi rõ kết quả học tập môn Toán của bạn An trong hai năm lớp 9 và lớp 10 như sau:
Lớp 9: \(\begin{array}{*{20}{l}}7&8&7&5&6&7&8&{9.}\end{array}\)
Lớp 10: \(\begin{array}{*{20}{l}}5&8&9&3&7&8&{10}&{9.}\end{array}\)
Hãy nhận xét xem trong hai năm học lớp 9 và lớp 10 thì năm nào là bạn An học Toán ổn định hơn?
Số liệu sau đây cho biết số con được sinh ra trong 20 hộ gia đình được khảo sát ở một địa phương: \[\begin{array}{*{20}{l}}2&2&3&5&2&4&3&2&1&9&5&3&2&4&1&0&3&2&1&{6.}\end{array}\]
Tìm độ lệch chuẩn của mẫu số liệu đã cho?
Mẫu số liệu sau là thống kê số tiền (triệu đồng) mua phân bón \(XYZ\) trong một vụ mùa của 15 hộ nông dân ở một khu vực nông thôn được khảo sát:
\(\begin{array}{*{20}{l}}{2,4}&{1,2}&{1,1}&{0,8}&{3,5}&{1,6}&{1,8}&{1,2}&{1,3}&{0,7}&{4,1}&{4,8}&{3,6}&{2,9}&{2,6}\end{array}\)
Tìm độ lệch chuẩn của mẫu số liệu đã cho?
Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày.
7 | 8 | 22 | 20 | 15 | 18 | 19 | 13 | 11 |
Tìm khoảng tứ phân vị của mẫu số liệu này
Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày
12 | 7 | 10 | 9 | 12 | 9 | 10 | 11 | 10 | 14 |
Tìm khoảng tứ phân vị của mẫu số liệu này






