Đề kiểm tra Các khái niệm mở đầu (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hình bình hành \(ABCD\) tâm \(O\). Các véctơ ngược hướng với ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
![]()
Cho hình chữ nhật \(ABCD\) có \(AB = 3,AD = 4\). Khẳng định nào sau đây đúng ?
\(\left| {\overrightarrow {{\rm{AC}}} } \right| = \left| {\overrightarrow {{\rm{BD}}} } \right|\).
\(\left| {\overrightarrow {{\rm{CD}}} } \right| = \left| {\overrightarrow {{\rm{BC}}} } \right|\).
\(\left| {\overrightarrow {{\rm{AC}}} } \right| = \left| {\overrightarrow {{\rm{AB}}} } \right|\).
.
Cho hình chữ nhật ABCD tâm \(I\),\(AB = 3,BC = 4\). Khi đó là:
7.
.
5.
\[\frac{7}{2}.\]
Mệnh đề nào sau đây đúng?
Hai vectơ cùng phương thì chúng cùng hướng.
Hai vectơ cùng phương thì giá của chúng song song hoặc trùng nhau.
Hai vectơ có giá vuông góc thì cùng phương.
Hai vectơ ngược hướng với 1 vectơ thứ ba thì cùng phương.
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Đẳng thức nào sau đây là sai?
\(\overrightarrow {AB} = \overrightarrow {ED} .\)
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AF} } \right|.\)
\(\overrightarrow {OD} = \overrightarrow {BC} .\)
\(\overrightarrow {OB} = \overrightarrow {OE} .\)
Cho hình bình hành \(ABCD\)tâm \(O\). Gọi \(P,Q,R\) lần lượt là trung điểm \(AB,BC,AD\). Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai:
Có 2 vectơ bằng \(\overrightarrow {PQ} \)
Có 4 vectơ bằng \(\overrightarrow {AR} \)
Có 3 vectơ bằng \(\overrightarrow {BO} \)
Có 5 vectơ bằng \(\overrightarrow {OP} \)
Cho hai điểm phân biệt \[A\] và \[B\]. Điều kiện để điểm \[I\] là trung điểm của đoạn thẳng \[AB\] là:
\(\overrightarrow {IA} = \overrightarrow {BI} \).
\(\overrightarrow {AI} = \overrightarrow {BI} \).
\(IA = IB\).
\(\overrightarrow {IA} = \overrightarrow {IB} \).
Cho hình thoi \(ABCD\) có tâm \(I\). Hãy cho biết số khẳng định đúng trong các khẳng định sau?a) \(\overrightarrow {AB} = \overrightarrow {BC} \) b) \(\overrightarrow {AB} = \overrightarrow {DC} \) c) \(\overrightarrow {IA} = \overrightarrow {IO} \)d) \(\overrightarrow {IB} = \overrightarrow {IA} \) e) \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\) f) \(2\left| {\overrightarrow {IA} } \right| = \left| {\overrightarrow {BD} } \right|\)
3.
4.
5.
6.
Cho\[3\] điểm \(A\),\(B\),\(C\) không thẳng hàng, \[M\] là điểm bất kỳ. Mệnh đề nào sau đây đúng?
\[\forall M{\rm{,}}\overrightarrow {MA} = \overrightarrow {MB} \].
\[\exists M{\rm{,}}\overrightarrow {MA} = \overrightarrow {MB} = \overrightarrow {MC} \].
\[\forall M{\rm{,}}\overrightarrow {MA} \ne \overrightarrow {MB} \ne \overrightarrow {MC} \].
\[\exists M{\rm{,}}\overrightarrow {MA} = \overrightarrow {MB} \].
Cho hai điểm phân biệt \[A,B\]. Số vectơ ( khác\[\overrightarrow 0 \]) có điểm đầu và điểm cuối lấy từ các điểm \[A,B\] là:
\[2\].
\[6\].
\[13\].
\[12\].
Gọi \[C\] là trung điểm của đoạn \[AB\]. Hãy chọn khẳng định đúng trong các khẳng định sau:
\[\overrightarrow {CA} = \overrightarrow {CB} \].
\[\overrightarrow {AB} \] và \[\overrightarrow {AC} \] cùng hướng.
\[\overrightarrow {AB} \] và \[\overrightarrow {CB} \] ngược hướng.
\[\left| {\overrightarrow {AB} } \right| = \overrightarrow {CB} \].
Cho hình bình hành \[ABCD\]. Các vectơ là vectơ đối của vectơ \[\overrightarrow {AD} \] là
\[\overrightarrow {AD} ,\overrightarrow {BC} \].
\[\overrightarrow {BD} ,\overrightarrow {AC} \].
\[\overrightarrow {DA} ,\overrightarrow {CB} \].
\[\overrightarrow {AB} ,\overrightarrow {CB} \].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác \(ABC\). Hãy dựng các điểm \(M,N\) sao cho \(\overrightarrow {AM} = \overrightarrow {BC} \), \(\overrightarrow {AN} = \overrightarrow {CB} \). Khi đó:
a) \(\overrightarrow {AM} \) ngược hướng với \(\overrightarrow {BC} \)
b) \(ABCM\) là hình bình hành
c) \(ACBN\) là hình bình hành
d) \(\overrightarrow {AM} ,\overrightarrow {AN} \) là hai vectơ đối nhau
Cho \(\Delta ABC\) có trực tâm \(H\) và \(O\) là tâm đường tròn ngoại tiếp tam giác. Gọi \({B^\prime }\) là điểm đối xứng của \(B\) qua \(O\). Khi đó:
a) \({B^\prime }C \bot BC\)
b) \({B^\prime }C//AB\)
c) tứ giác \(A{B^\prime }CH\) là hình bình hành.
d) \(\overrightarrow {AH} = \overrightarrow {{B^\prime }C} ;\overrightarrow {A{B^\prime }} = \overrightarrow {HC} \)
Cho tứ giác \(ABCD\). Khi đó:
a) Có 5 vectơ liên quan đến điểm \(A\)
b) Có 4 vectơ liên quan đến điểm \(B\) mà không liên quan đến \(A\)
c) Có 2 vectơ liên quan đến hai điểm \(C,D\)
d) Có 10 vectơ (khác \(\vec 0)\) có điểm đầu và điểm cuối là các điểm \(A,B,C,D\)?
Cho \(\Delta ABC\) đều cạnh \(a\), trực tâm \(H\). Khi đó:
a) \(AH \bot BC\)
b) \(AH = \frac{{a\sqrt 3 }}{2}\)
c) \(\overrightarrow {HA} = \overrightarrow {HB} = \overrightarrow {HC} \)
d) \(|\overrightarrow {HA} | = |\overrightarrow {HB} | = |\overrightarrow {HC} | = \frac{{a\sqrt 3 }}{3}{\rm{. }}\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
Bác Ba có số tiền là 20 triệu đồng.
Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.
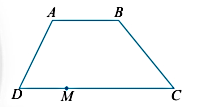
Cho hình thang ABCD có hai cạnh đáy là AB và DC (Hình 15).
Điểm M nằm trên đoạn DC. Gọi tên các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \).
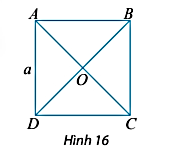
Cho hình vuông ABCD có tâm O và có cạnh bằng a (Hình 16). Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
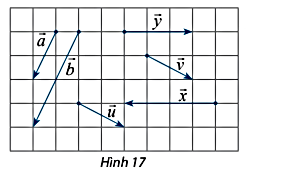
Hãy chỉ ra các cặp vectơ cùng hướng, trong Hình 17.
Gọi O là tâm hình lục giác đều ABCDEF. Tìm các vectơ khác vectơ \(\vec 0\) và cùng hướng với vectơ\(\overrightarrow {\;OA} \).
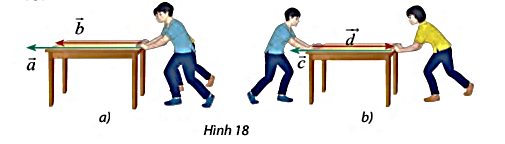
Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong Hình 18.