Đề kiểm tra Các khái niệm mở đầu (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Xét các mệnh đề sau
(I): Véc tơ – không là véc tơ có độ dài bằng \(0\).
(II): Véc tơ – không là véc tơ có nhiều phương.
Chỉ (I) đúng.
Chỉ (II) đúng.
(I) và (II) đúng.
(I) và (II) sai.
Cho tam giác đều \[ABC\] cạnh \(a\), mệnh đề nào sau đây đúng?
\(\left| {\overrightarrow {AC} } \right| = \overrightarrow {BC} \).
\(\overrightarrow {AC} = a\).
\(\overrightarrow {AB} = \overrightarrow {AC} \).
\(\left| {\overrightarrow {AB} } \right| = a\).
Cho M là một điểm thuộc đoạn thẳng AB sao cho AB = 3AM. Hãy tìm khẳng định sai?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. 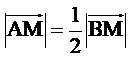 .
.
Cho hình bình hành \(ABCD\). Khẳng định nào sau đây đúng?
\[\overrightarrow {AD} \]= \[\overrightarrow {BC} \].
\[\overrightarrow {AB} \]= \[\overrightarrow {AC} \].
\[\overrightarrow {AC} \]= \[\overrightarrow {DB} \].
\[\overrightarrow {AB} \]= \[\overrightarrow {CD} \].
Cho tứ giác đều ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Mệnh đề nào sau đây là sai?
\(\overrightarrow {MN} = \overrightarrow {QP} \)
\(\left| {\overrightarrow {QP} } \right| = \left| {\overrightarrow {MN} } \right|\)
\(\overrightarrow {MQ} = \overrightarrow {NP} \)
\(\left| {\overrightarrow {MN} } \right| = \left| {\overrightarrow {AC} } \right|\)
Cho ba điểm A, B, C phân biệt và thẳng hàng. Mệnh đề nào sau đây đúng?
\(\overrightarrow {AB} = \overrightarrow {BC} \)
\(\overrightarrow {CA} \) và \(\overrightarrow {CB} \) cùng hướng
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) ngược hướng
\(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) cùng phương
Gọi \(M,\;N\) lần lượt là trung điểm của các cạnh \(AB,\;AC\) của tam giác đều \(ABC\). Đẳng thức nào sau đây đúng?
\(\overrightarrow {MA} = \overrightarrow {MB} .\)
\(\overrightarrow {AB} = \overrightarrow {AC} .\)
\(\overrightarrow {MN} = \overrightarrow {BC} .\)
\(\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {MN} } \right|.\)
Cho tứ giác \(ABCD\). Điều kiện nào là điều kiện cần và đủ để \(\overrightarrow {AB} = \overrightarrow {CD} \)?
\(ABCD\) là hình bình hành.
\(ABDC\) là hình bình hành.
\(AD\) và \(BC\) có cùng trung điểm.
\(AB = CD.\)
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA. Xác định các vectơ cùng phương với \(\overrightarrow {MN} \).
\(\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {AP} ,\overrightarrow {PA} ,\overrightarrow {PC} ,\overrightarrow {CP} \)
\(\overrightarrow {NM} ,\overrightarrow {BC} ,\overrightarrow {CB} ,\overrightarrow {PA} ,\overrightarrow {AP} \)
\(\overrightarrow {NM} ,\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {AP} ,\overrightarrow {PA} ,\overrightarrow {PC} ,\overrightarrow {CP} \)
\(\overrightarrow {NM} ,\overrightarrow {BC} ,\overrightarrow {CA} ,\overrightarrow {AM} ,\overrightarrow {MA} ,\overrightarrow {PN} ,\overrightarrow {CP} \)
Cho ba điểm A, B, C cùng nằm trên một đường thẳng. Các vectơ \(\overrightarrow {AB} ,\overrightarrow {BC} \) cùng hướng khi và chỉ khi:
Điểm B thuộc đoạn AC
Điểm A thuộc đoạn BC
Điểm C thuộc đoạn AB
Điểm A nằm ngoài đoạn BC
Cho tam giác đều cạnh 2a. Đẳng thức nào sau đây là đúng?
\(\overrightarrow {AB} = \overrightarrow {AC} \)
\(\overrightarrow {AB} = 2a\)
\(\left| {\overrightarrow {AB} } \right| = 2a\)
\(\overrightarrow {AB} = AB\)
Cho hình thoi tâm O, cạnh bằng a và \(\widehat A = 60^\circ \). Kết luận nào sau đây là đúng?
\(\left| {\overrightarrow {AO} } \right| = \frac{{a\sqrt 3 }}{2}\)
\(\left| {\overrightarrow {OA} } \right| = a\)
\(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right|\)
\(\left| {\overrightarrow {OA} } \right| = \frac{{a\sqrt 2 }}{2}\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tam giác \(ABC\) có \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(AC\). Lấy điểm \(P\) đối xứng với điểm \(M\) qua \(N\). Khi đó:
a) \(MN = BC\)
b) \(|\overrightarrow {MP} | = |\overrightarrow {BC} |\)
c) \(\overrightarrow {MN} \) và \(\overrightarrow {BC} \) ngược hướng
d) \(\overrightarrow {MP} = \overrightarrow {BC} \).
Cho \(\Delta ABC\), gọi \(M,N,P\) lần lượt là trung điểm của \(BC,CA,AB\). Khi đó:
a) vectơ \(\overrightarrow {AB} \) cùng phương với vectơ \(\overrightarrow {MN} \)
b) Có 6 vectơ khác vectơ không và cùng phương với \(\overline {AB} \) có điểm đầu, điểm cuối lấy từ các điểm đã cho.
c) vectơ\(\overrightarrow {AP} \)ngược hướng vectơ\(\overrightarrow {PB} \)
d) Có 3 vectơ khác vectơ không và cùng hướng với \(\overrightarrow {AB} \) có điểm đầu và điểm cuối lấy từ các điểm đã cho.
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Khi đó:
a) vectơ \(\overrightarrow {OA} \) cùng phương với \(\overrightarrow {OD} \)
b) Có 9 vectơ khác vectơ không và cùng phương với vectơ \(\overrightarrow {OA} \).
c) vectơ \(\overrightarrow {AB} \)ngược hướng \(\overrightarrow {OC} \)
d) Có 3 vectơ khác vectơ không và cùng hướng với vectơ \(\overrightarrow {AB} \).
Cho tứ giác \(ABCD\). Gọi \(M,N,P,Q\) lần lượt là trung điểm \(AB,BC\),\(CD,DA\). Khi đó:
a) \(MN\) là đường trung bình của tam giác \(ACD\)
b) \(PQ = \frac{1}{2}AC\)
c) Tứ giác \(MNPQ\) là hình thang
d) \(\overrightarrow {MN} = \overrightarrow {QP} \)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Cho tứ giác \(ABCD\). Gọi \(M,N,P,Q\) lần lượt là trung điểm của \(AB,BC,CD,DA\). Từ các điểm đã cho tìm các vec tơ cùng hướng với vec tơ \(\overrightarrow {MN} \)
Cho hình bình hành \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(DC,AB.P\) là giao điểm của \(AM,DB\) và \(Q\) là giao điểm của \(CN,DB\). Khi đó \(\overrightarrow {DP} = \overrightarrow {PQ} = \overrightarrow {QB} \) đúng hay sai?
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB} \) = \(\overrightarrow {DC} \)
Chứng minh rằng, tứ giác \(ABCD\) là hình bình hành khi và chỉ khi \(\overrightarrow {BC} = \overrightarrow {AD} \).
Cho hình vuông \(ABCD\)có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S chứa tất cả các vectơ khác vectơ \(\overrightarrow 0 \), có điểm đầu và điểm cuối thuộc tập hợp \(\left\{ {A,B,C,D,O} \right\}\). Hãy chia tập S thành các nhóm sao cho hai vectơ thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
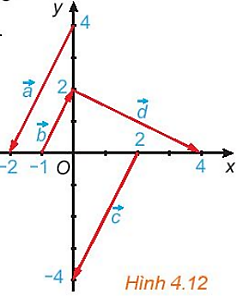
Trong Hình 4.12, hãy chỉ ra các vectơ cùng phương,