Đề kiểm tra Bài tập cuối chương V (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho bảng phân bố tần số sau: khối lượng \(20\) học sinh lớp \(10A\)
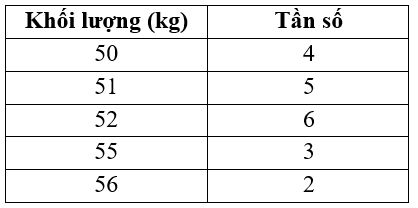
Số trung bình cộng \(\overline x \) của bảng số liệu đã cho là
\(\overline x = 53\).
\(\overline x = 52,8\).
\(\overline x = 52,2\).
\(\overline x = 52\).
Điểm thi học kì của một học sinh như sau: \[4;\,6;\,2;\,7;\,3;\,5;\,9;\,8;\,7;\,10;\,9\]. Số trung bình và số trung vị lần lượt là
\(6,22\)và \(7\).
\(7\) và \(6\).
\(6,36\) và \(7\).
\(6\) và \(6\).
Một nhóm \(10\) học sinh tham gia một kỳ thi. Số điểm thi của \(10\) học sinh đó được sắp xếp từ thấp đến cao như sau (thang điểm 10): \(0;1;2;4;4;5;7;8;8;9\). Tìm số trung vị của mẫu số liệu.
\(5\).
\(5,5\).
\(4,5\).
\(4\).
Độ dài các cạnh của một đám vườn hình chữ nhật là \[x = 7,8\,{\rm{m}} \pm 2\,{\rm{cm}}\] và \[y = 25,6\,{\rm{m}} \pm 4\,{\rm{cm}}\]. Cách viết chuẩn của diện tích (sau khi quy tròn) là
\[200\,{{\rm{m}}^2} \pm 0,9\,{{\rm{m}}^2}\].
\[199\,{{\rm{m}}^2} \pm 0,8\,{{\rm{m}}^2}\].
\[199\,{{\rm{m}}^2} \pm 1\,{{\rm{m}}^2}\].
\[200\,{{\rm{m}}^2} \pm 1\,{{\rm{m}}^2}\].
Chiều dài gần đúng của một cái bàn học là \[a = 1,238\] (m) với độ chính xác \[d = 0,01\] (m). Hãy viết số quy tròn của số \[a\]?
Số quy tròn của \[a\] là \[1,2\] (m).
Số quy tròn của \[a\] là \[1,23\] (m).
Số quy tròn của \[a\] là \[1,24\] (m).
Số quy tròn của \[a\] là \[1,248\] (m).
Số tiền quỹ lớp 10A còn lại là \[a = 1\,647\,500\] (đồng) với độ chính xác \[d = 500\] (đồng). Hãy viết số quy tròn của số \[a\]?
Số quy tròn của \[a\] là \[1\,648\,000\] (đồng).
Số quy tròn của \[a\] là \[1\,647\,000\] (đồng).
Số quy tròn của \[a\] là \[1\,649\,000\] (đồng).
Số quy tròn của \[a\] là \[1\,650\,000\] (đồng).
Cho số \[\overline a = 17658\,\, \pm \,\,16\]. Số quy tròn của số gần đúng \(17658\) là
\[18000\]
\[17800\]
\[17600\]
\[17700\].
Cho số \(\overline a = 4,1356 \pm 0,001\). Số quy tròn của số gần đúng \(4,1356\) là
\(4,135\).
\(4,13\).
\(4,136\).
\(4,14\).
Cho giá trị gần đúng của \[\frac{8}{{17}}\] là \[0,47\]. Sai số tuyệt đối của \[0,47\] là
\[0,001\].
\[0,003\].
\[0,002\].
\[0,004\].
Đo chiều dài của một cây thước, ta được kết quả \[\overline a = 45 \pm 0,3\,({\rm{cm}})\]. Khi đó sai số tuyệt đối của phép đo được ước lượng là
\({\Delta _{45}} = 0,3\).
\({\Delta _{45}} \le 0,3\).
\({\Delta _{45}} \le - 0,3\).
\({\Delta _{45}} = - 0,3\).
Tính phương sai của dãy số liệu: \(1,3,3,5,7,9,10,11,11,11.\)
\(\frac{{71}}{{10}}\).
\(\frac{{1329}}{{10}}\).
\(\frac{{710}}{{10}}\).
\(\frac{{1329}}{{100}}\).
Cho mẫu số liệu thống kê \[\left\{ {1;2;3;\,4;\,5;\,6;7;\,8;\,9} \right\}\].Tính (gần đúng) độ lệch chuẩn của mẫu số liệu trên?
\(2,45\).
\(2,58\).
\(6,67\).
\(6,0\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Mẫu số liệu sau cho biết khối lượng (kg) của 15 người trong độ tuổi ngoài
\(40\,\,\,42\,\,\,42\,\,\,43\,\,\,44\,\,\,45\,\,\,46\,\,\,47\,\,\,48\,\,\,50\,\,\,51\,\,\,53\,\,\,55\,\,\,56\,\,\,60.\)
Khi đó:
a) Khoảng biến thiên \(R = 20\).
b) Trung vị của mẫu là \(45\).
c) Tứ phân vị thứ nhất là \({Q_1} = 45\).
d) Khoảng tứ phân vị là \(\Delta Q = 10\).
Mỗi mẫu số liệu sau ghi rõ số bàn thắng của hai đội tuyển Việt Nam và Thái Lan trong một năm dương lịch khi thi đấu với các đội bóng khác ở khu vực.
Số bàn thắng đội tuyển Việt Nam: \(\begin{array}{*{20}{l}}4&3&2&1&6&2&3&3&2&2&3&5\end{array}\).
Số bàn thắng đội tuyển Thái Lan: \(\begin{array}{*{20}{l}}6&8&0&0&3&4&3&2&3&1&1&5\end{array}\).
Khi đó:
a) Số bàn thắng trung bình của đội tuyển Việt Nam và đội tuyển Thái Lan là không bằng nhau
b) Xét mẫu số liệu về số bàn thắng của đội tuyển Việt Nam có độ lệch chuẩn là: \({s_1} \approx 1,354\) (bàn).
c) Xét mẫu số liệu về số bàn thắng của đội tuyển Thái Lan có phương sai là: \(s_2^2 = 5,5\)
d) Khả năng ghi bàn của đội tuyển Thái Lan có tính ổn định hơn so với đội tuyển Việt Nam
Điểm trung bình môn học kì của hai bạn An và Bình được cho như bảng sauKhi đó:
Khi đó:

a) Điểm trung bình môn học kì của hai bạn đều là 8,0.
b) Khoảng biến thiên điểm của bạn An là \({R_1} = 0,7\).
c) Khoảng biến thiên điểm của bạn Bình là \({R_2} = 3\).
d) bạn An học đều hơn bạn Bình
Điểm kiểm tra học kì môn Toán của các bạn Tổ 1, Tổ 2 lớp 12B được cho như sau: Khi đó:

a) Điểm trung bình môn học kì của các bạn tổ 1 và tổ 2 đều là 7.
b) Đối với Tổ 1: điểm kiểm tra thấp nhất, cao nhất tương ứng là 7;9
c) Đối với Tổ 2: điểm kiểm tra thấp nhất, cao nhất tương ứng là 6;10.
d) Tổ 1 học đều hơn Tổ 2.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Hàm lượng Natri (đơn vị miligam, \(1mg = 0,001\;g\)) trong \(100\;g\) một số loại ngũ cốc được cho như sau:
0 | 340 | 70 | 140 | 200 | 180 | 210 | 150 | 100 | 130 |
140 | 180 | 190 | 160 | 290 | 50 | 220 | 180 | 200 | 210 |
Hãy tìm các tứ phân vị?
Bảng sau đây cho biết số lần học tiếng Anh trên internet trong một tuần của một học sinh lớp 10:
Số lần | 0 | 1 | 2 | 3 | 4 | 5 |
Số học sinh | 2 | 4 | 6 | 12 | 8 | 3 |
Hãy tìm các tứ phân vị cho mẫu số liệu này.
Hàm lượng Natri (đơn vị \(mg\)) trong \(100\;g\) một số loại ngũ cốc được cho như sau:
\(\begin{array}{*{20}{l}}0&{340}&{70}&{140}&{200}&{180}&{210}&{150}&{100}&{130}\\{140}&{180}&{190}&{160}&{290}&{50}&{220}&{180}&{200}&{210.}\end{array}\)
Tìm giá trị bất thường trong mẫu số liệu trên bằng cách sử dụng biểu đồ hộp.
Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ
\(\begin{array}{*{20}{l}}{163}&{159}&{172}&{167}&{165}&{168}&{170}&{161.}\end{array}\)
Tìm khoảng biến thiên của mẫu số liệu này.
Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của An
12 7 10 9 12 9 10 11 10 14.
Tìm khoảng tứ phân vị cho mẫu số liệu này.
Thời gian truy cập internet (đơn vị giờ) trong một ngày của một số học sinh lớp 10 được cho như sau:
Tìm mốt cho mẫu số liệu này.


