Đề kiểm tra Bài tập cuối chương IV (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho tam giác \(ABC\) biết \(AB = 8,AC = 9,BC = 11\). Gọi \(M\) là trung điểm \(BC\) và \(N\) là điểm trên đoạn \(AC\) sao cho \(AN = x\,(0 < x < 9)\). Hệ thức nào sau đây đúng?
\(\overrightarrow {MN} = \left( {\frac{1}{2} - \frac{x}{9}} \right)\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} \)
\(\overrightarrow {MN} = \left( {\frac{x}{9} - \frac{1}{2}} \right)\overrightarrow {CA} + \frac{1}{2}\overrightarrow {BA} \)
\(\overrightarrow {MN} = \left( {\frac{x}{9} + \frac{1}{2}} \right)\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \)
\(\overrightarrow {MN} = \left( {\frac{x}{9} - \frac{1}{2}} \right)\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \)
Cho tam giác \(ABC\) có trọng tâm \(G\). Gọi các điểm \(D,E,F\) lần lượt là trung điểm của các cạnh \(BC,CA\) và \(AB\). Trong các khẳng định sau, khẳng định nào đúng?
\(\overrightarrow {AG} = \frac{1}{2}\overrightarrow {AE} + \frac{1}{2}\overrightarrow {AF} \)
\(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AE} + \frac{1}{3}\overrightarrow {AF} \)
\(\overrightarrow {AG} = \frac{3}{2}\overrightarrow {AE} + \frac{3}{2}\overrightarrow {AF} \)
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} + \frac{2}{3}\overrightarrow {AF} \)
Cho \(\Delta ABC\). Xác định điểm M sao cho:\(\overrightarrow {MA} + 2\overrightarrow {MB} = \overrightarrow {CB} \).
M là trung điểm cạnh AB
M là trung điểm cạnh BC
M chia đoạn AB theo tỉ số 2
M là trọng tâm \(\Delta ABC\)
Cho \(\Delta ABC\) có trọng tâm G, điểm M thỏa mãn \(2\overrightarrow {MA} + \overrightarrow {MB} + 3\overrightarrow {MC} = \overrightarrow 0 \). Khi đó điểm M thỏa mãn hệ thức nào sau đây?
\(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {BC} \)
\(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {CA} \)
\(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {AB} \)
\(\overrightarrow {GM} = \frac{1}{3}\overrightarrow {CB} \)
Gọi G là trọng tâm \(\Delta ABC\). Nối điểm M thỏa mãn hệ thức \(\overrightarrow {MA} + \overrightarrow {MB} + 4\overrightarrow {MC} = \overrightarrow 0 \) thì M ở vị trí nào trong hình vẽ: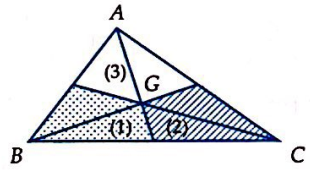
Miền (1)
Miền (2)
Miền (3)
Ở ngoài \(\Delta ABC\)
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Điểm M thỏa mãn đẳng thức \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 4\overrightarrow {AM} \). Khi đó điểm M trùng với điểm:
O
I là trung điểm đoạn OA
I là trung điểm đoạn OC
C
Cho ba điểm \(O,{\rm{ }}A,{\rm{ }}B\) không thẳng hàng. Điều kiện cần và đủ để tích vô hướng \(\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right).\overrightarrow {AB} = 0\) là
tam giác \(OAB\) đều.
tam giác \(OAB\) cân tại \(O.\)
tam giác \(OAB\) vuông tại \(O.\)
tam giác \(OAB\) vuông cân tại \(O.\)
Cho hình chữ nhật \(ABCD\) có \(AB = 8,{\rm{ }}AD = 5.\) Đẳng thức nào sau đây đúng?
\[\overrightarrow {AB} .\overrightarrow {BD} = 62.\]
\[\overrightarrow {AB} .\overrightarrow {BD} = 64.\]
\[\overrightarrow {AB} .\overrightarrow {BD} = - 62.\]
\[\overrightarrow {AB} .\overrightarrow {BD} = - 64.\]
Cho hình thoi \(ABCD\) có \(AC = 8\) và \(BD = 6.\) Đẳng thức nào sau đây đúng?
\[\overrightarrow {AB} .\overrightarrow {AC} = 24.\]
\[\overrightarrow {AB} .\overrightarrow {AC} = 26.\]
\[\overrightarrow {AB} .\overrightarrow {AC} = 28.\]
\[\overrightarrow {AB} .\overrightarrow {AC} = 32.\]
Cho tam giác \(ABC\). Tập hợp các điểm \(M\) thỏa mãn \(\overrightarrow {MA} \left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\) là:
một điểm.
đường thẳng.
đoạn thẳng.
đường tròn.
Tìm tập các hợp điểm \(M\) thỏa mãn \[\overrightarrow {MB} \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\] với \(A,{\rm{ }}B,{\rm{ }}C\) là ba đỉnh của tam giác.
một điểm.
đường thẳng.
đoạn thẳng.
đường tròn.
Cho tam giác vuông cân \(ABC\) với \(AB = AC = a\). Khi đó \(\left| {2\overrightarrow {AB} + \overrightarrow {AC} } \right|\) bằng
\(a\sqrt 3 \).
\(a\sqrt 5 \).
\(5a\).
\(2a\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tứ giác \(ABCD\). Gọi \(I,J\) lần lượt là trung điểm \(AB\) và \(CD,K\) là trung điểm \(IJ,M\) là điểm bất kì. Khi đó:
a) \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {IJ} \)
b) \(\overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {IJ} \)
c) \(\overrightarrow {MI} + \overrightarrow {MJ} = \overrightarrow {MK} \)
d) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MK} \)
Cho tam giác \(ABC\) có \(M\) là trung điểm \(BC\). Gọi \(G\) là trọng tâm, \(H\) là trực tâm, \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\), \(A{A^\prime }\) là đường kính của \((O)\). Khi đó:
a) \(\overrightarrow {BH} = \overrightarrow {{A^\prime }C} \)
b) \(\overrightarrow {AH} = 2\overrightarrow {OM} \)
c) \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 3\overrightarrow {HO} \)
d) \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OH} \]
Cho tam giác \(ABC\) đều có cạnh \(a\), có trọng tâm \(G\). Khi đó:
a) \(\overrightarrow {AB} \cdot \overrightarrow {AC} = \frac{{{a^2}}}{2}\)
b) \(\overrightarrow {AG} \cdot \overrightarrow {AC} = \frac{{{a^2}}}{4}\)
c)
d) \(\overrightarrow {AG} \cdot \overrightarrow {GC} = \frac{{{a^2}}}{6}\)
Cho tam giác \(ABC\) có . Gọi \(I\) là trung điểm đoạn thẳng \(BC\). Điểm \(J\) thuộc đoạn \(AC\) thỏa mãn: \(12AJ = 7AC\). Khi đó:
a) \(\overrightarrow {AB} \cdot \overrightarrow {AC} = 4{a^2}\)
b) \(\overrightarrow {AI} = \frac{3}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} \)
c) \(\overrightarrow {BJ} = - \overrightarrow {AB} + \frac{7}{{12}}\overrightarrow {AC} \)
d) \(AI \bot BJ\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Cho tam giác \(ABC\) có hai trung tuyến \(AK\) và \(BM\). Hãy phân tích vectơ \(\overrightarrow {AB} \) theo hai vectơ \(\overrightarrow {AK} \) và \(\overrightarrow {BM} \).
Cho tam giác \(ABC\). Gọi \(G\) là trọng tâm của \(\Delta ABC\). Cho điểm \(M\) sao cho \(|\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} | = 6\), khi đó điểm \(M\) thuộc đường tròn có bán kính bằng bao nhiêu?
Cho \(\Delta ABC\) đều cạnh là 3. Điểm \(M\) thỏa mãn: \(2M{A^2} + M{B^2} + M{C^2} = 18\), khi đó tập hợp điểm \(M\) thuộc đường tròn có bán kính bằng bao nhiêu?
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AC = 7\;cm\) và \(BC = 14\;cm\).
Tính côsin của góc giữa hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \).
Cho hình vuông \(ABCD\) cạnh bằng 3. Trên cạnh \(AB\) lấy điểm \(M\) sao cho \(BM = 1\), trên cạnh \(CD\) lấy điểm \(N\) sao cho \(DN = 1\) và \(P\) là trung điểm \(BC\). Tính \(\cos \widehat {MNP}\).
Cho tam giác \(ABC\). Gọi \(M,N,E\) lần lượt là trung điểm của \(BC,CA,AB\). Tính: \(\overrightarrow {AM} \cdot \overrightarrow {BC} + \overrightarrow {BN} \cdot \overrightarrow {CA} + \overrightarrow {CE} \cdot \overrightarrow {AB} \).


