30 câu Trắc nghiệm Toán 10 Kết nối tri thức Bài tập cuối chương 4 có đáp án
30 câu hỏi
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
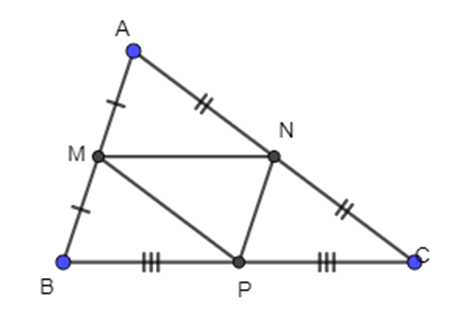
Phát biểu nào dưới đây là sai.
\(\overrightarrow {MN} = \overrightarrow {PC} \);
\(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \);
\(\overrightarrow {MB} = \overrightarrow {AM} \);
\(\overrightarrow {MN} = \overrightarrow {PB} \).
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
\(\overrightarrow {DC} \);
\(\overrightarrow {AD} \);
\(\overrightarrow {CB} \);
\(\overrightarrow {BA} \).
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
P(0; 13);
Q(1; -8);
H(2; 1);
K(3; 1).
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
\(\left| {\overrightarrow {AM} } \right| = \sqrt {53} \)cm
\(\left| {\overrightarrow {AM} } \right| = 3\) cm
\(\left| {\overrightarrow {AM} } \right| = \frac{{\sqrt {53} }}{2}\) cm
\(\left| {\overrightarrow {AM} } \right| = \frac{3}{2}\) cm
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
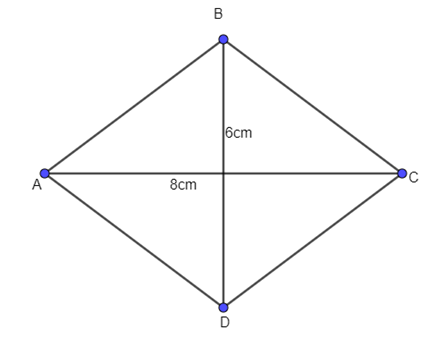
10 cm;
3 cm;
4 cm;
5cm.
Vectơ có điểm đầu là P điểm cuối là Q được kí hiệu là:
\(\overrightarrow {PQ} \);
\(\overrightarrow {QP} \);
PQ;
\(\overline {PQ} \).
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
\(G\left( {\frac{1}{3};1} \right)\);
G(1; 3);
G(2; -3);
G(1; 1).
Khi nào tích vô hướng của hai vecto \(\overrightarrow u ,\overrightarrow v \) là một số dương.
Khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) là một góc tù;
Khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) là góc bẹt;
Khi và chỉ khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) bằng 00;
Khi góc giữa hai vectơ \(\overrightarrow u ,\overrightarrow v \) là góc nhọn hoặc bằng 00.
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
(-1; 7);
(4; 10);
(1; 12);
Không xác định được vị trí của tàu.
Trong mặt phẳng tọa độ Oxy cho các điểm A(11; –2), B(4; 10); C(-2; 2); D(7; 6); Hỏi G(3; 6) là trọng tâm của tam giác nào trong các tam giác sau đây?
Tam giác ABD
Tam giác ABC
Tam giác ACD
Tam giác BCD
Cho hình vẽ sau:
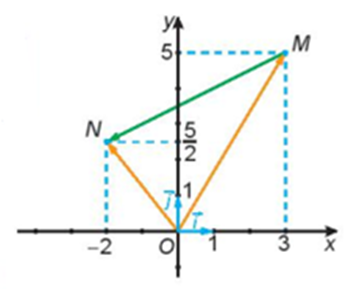
Hãy biểu thị mỗi vecto \(\overrightarrow {OM} ,\overrightarrow {ON} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \).
\(\overrightarrow {OM} = 3\overrightarrow i + 5\overrightarrow j \) và \(\overrightarrow {ON} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j \);
\(\overrightarrow {OM} = 5\overrightarrow i + 3\overrightarrow j \) và \(\overrightarrow {ON} = - 2\overrightarrow i + \frac{5}{2}\overrightarrow j \);
\(\overrightarrow {OM} = 3\overrightarrow i + 5\overrightarrow j \) và \[\overrightarrow {ON} = - \frac{5}{2}\overrightarrow i + 2\overrightarrow j \];
\(\overrightarrow {OM} = 3\overrightarrow i - 5\overrightarrow j \) và \(\overrightarrow {ON} = - 2\overrightarrow i - \frac{5}{2}\overrightarrow j \).
Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
\(\overrightarrow x \)(-1; 3); \(\overrightarrow y \left( {2; - \frac{1}{3}} \right)\) ; \(\overrightarrow z \left( { - \frac{2}{5};\frac{1}{5}} \right)\); \(\overrightarrow {\rm{w}} \)(4; -2).
Có 1 cặp;
Có 3 cặp;
Có 4 cặp;
Có 0 cặp.
Cho tam giác ABC có bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?
3;
4;
5;
6.
Điền từ thích hợp vào dấu (…) để được mệnh đề đúng. “Hai vectơ ngược hướng thì …”:
có giá song song;
cùng phương;
có độ dài bằng nhau;
có giá trùng nhau.
Mệnh đề nào sau đây là đúng?
Có duy nhất một vectơ cùng phương với mọi vec tơ;
Có vô số vectơ cùng phương với mọi vectơ;
Không có vectơ nào cùng phương với mọi vectơ;
Có ít nhất hai vectơ cùng phương với mọi vectơ.
Cho hình vẽ:
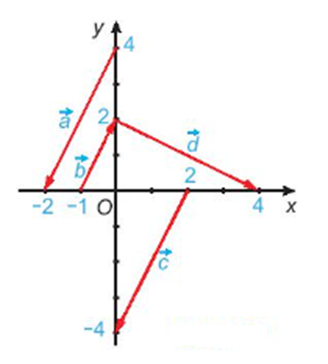
Có bao nhiêu cặp vectơ không cùng phương trên hình vẽ?
3;
2;
1;
0.
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 5\overrightarrow i + 6\overrightarrow j .\) Khi đó tọa độ của vectơ \(\overrightarrow u \)là:
\(\overrightarrow u \)(5; 6);
\(\overrightarrow u \)(-5; -6);
\(\overrightarrow u \)(6; -5);
\(\overrightarrow u \)(-5; 6).
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài \(\overrightarrow {BC} \) là:
5;
3;
\(\sqrt {13} \);
\(\sqrt {15} \).
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
M(1; 2);
M(-1; 2);
M(1; -2);
M(-1; -2)
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
Tam giác OMN là tam giác đều;
Tam giác OMN vuông cân tại M;
Tam giác OMN vuông cân tại N;
Tam giác OMN vuông cân tại O.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
C(0; 3);
C(-6; -5);
C(-12; -1);
C(0; 9).
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow b \left( {4; - 1} \right)\) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để \(\overrightarrow {MN} = \overrightarrow b \).
x = 0, y = 0;
x = \(\frac{1}{3}\), y = \(\frac{4}{3}\);
x = 0, y = \(\frac{4}{3}\);
x = \(\frac{4}{3}\), y = 0.
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
(10; 12);
(-2; 0);
(14; 15);
(12; 14).
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
\(\overrightarrow a \left( {1; - 1} \right)\) và \(\overrightarrow b \left( { - 1;1} \right)\).
\(\overrightarrow n \left( {1;1} \right)\) và \(\overrightarrow k \left( {2;0} \right)\).
\(\overrightarrow u \left( {2;3} \right)\) và \(\overrightarrow v \left( {4;6} \right)\).
\(z\left( {a;b} \right)\) và \[\overrightarrow t \left( { - b;a} \right)\].
Góc giữa vectơ \(\overrightarrow a \left( { - 1; - 1} \right)\) và vecto \(\overrightarrow b \left( { - 1;0} \right)\) có số đo bằng:
90°.
0°.
135°.
45°.
Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
\(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {45^0}.\)
\(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^0}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = {a^2}.\)
\(\overrightarrow {AC} .\overrightarrow {BD} = {a^2}\sqrt 2 .\)
\(\overrightarrow {BA} .\overrightarrow {BD} = - {a^2}.\)
Khi nào thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc?
\(\overrightarrow a \).\(\overrightarrow b \)= 1;
\(\overrightarrow a \).\(\overrightarrow b \)= - 1;
\(\overrightarrow a \).\(\overrightarrow b \)= 0;
a.b = -1.
Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn \(\overrightarrow {AB} .\overrightarrow {AC} = 2\)
\(\frac{{ - 2}}{3}\);
\(\frac{{ - 8}}{3}\);
\(\frac{{ - 5}}{3}\);
1.
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow u \left( {2;3x - 3} \right)\) và \(\overrightarrow v \left( { - 1; - 2} \right)\). Có bao nhiêu giá trị nguyên của x thỏa mãn \(\left| {\overrightarrow u } \right| = \left| {2\overrightarrow v } \right|\).
0;
1;
2;
3.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
P(0; 13);
Q(1; -8);
H(2; 1);
K(3; 1).


