Đề kiểm tra Bài tập cuối chương IV (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hình hộp \(ABCD \cdot A'B'C'D'\). Mặt phẳng \(\left( {AB'D'} \right)\) song song với mă̆t phẳng
\(\left( {ABCD} \right)\).
\(\left( {BCC'B'} \right)\).
\(\left( {BDA'} \right)\).
\(\left( {BDC'} \right)\).
Cho tam giác \(ABC\). Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh tam giác \(ABC\)?
\(4\).
\(3\).
\(2\).
\(1\).
Trong mp\(\left( \alpha \right)\), cho bốn điểm \(A\), \(B\), \(C\), \(D\) trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin mp\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên?
\[4\].
\[5\].
\[6\].
\[8\].
Cho năm điểm \(A\), \(B\), \(C\), \(D\), \(E\) trong đó không có bốn điểm nào ở trên cùng một mặt phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho?
\[10\].
\[12\].
\[8\].
\[14\].
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \(M\), \(N\)lần lượt là trung điểm \(AD\) và \(BC\).Giao tuyến của hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) là:
\(SD\).
\(SO\), \(O\) là tâm hình bình hành \(ABCD\).
\[SG\], \[G\] là trung điểm \[AB\].
\[SF\], \[F\] là trung điểm \[CD\].
Cho hình chóp S.ABCD có đáy là hình thang ABCD \(\left( {AD//BC} \right)\). Gọi \(M\) là trung điểm \(CD\). Giao tuyến của hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right)\) là:
\[SI\], \[I\] là giao điểm \[AC\] và \[BM\].
\[SJ\], \[J\] là giao điểm \[AM\] và \[BD\].
\[SO\], \[O\] là giao điểm \[AC\] và \[BD\].
\[SP\], \[P\] là giao điểm \[AB\] và \[CD\].
Cho hình hộp ABCD.A'B'C'D'. Mp\[(\alpha )\] qua \[AB\] cắt hình hộp theo thiết diện là hình gì?
Hình bình hành.
Hình thang.
Hình lục giác.
Hình chữ nhật.
Cho hình hộp ABCD.A'B'C'D'. Mặt phẳng \(\left( \alpha \right)\) đi qua một cạnh của hình hộp và cắt hình hộp theo thiết diện là một tứ giác \[\left( T \right)\]. Khẳng định nào sau đây đúng ?
\[\left( T \right)\]là hình chữ nhât.
\[\left( T \right)\]là hình bình hành.
\[\left( T \right)\]là hình thoi.
\[\left( T \right)\]là hình vuông.
Cho tam giác \[ABC\] ở trong mp\[\left( \alpha \right)\] và phương \[l\]. Biết hình chiếu của tam giác \[ABC\] lên mp\[\left( P \right)\]là một đoạn thẳng. Khẳng định nào sau đây đúng ?
\[\left( \alpha \right)//\left( P \right)\]
\[\left( \alpha \right) \equiv \left( P \right)\]
\[\left( \alpha \right)//l\] hoặc \[\left( \alpha \right) \supset l\]
\[A;B;C\] đều sai.
Phép chiếu song song theo phương \[l\] không song song với \[a\] hoặc \[b\], mặt phẳng chiếu là \[\left( P \right)\], hai đường thẳng \[a\] và \[b\] biến thành \[a'\] và \[b'\]. Quan hệ nào giữa \[a\] và \[b\]không được bảo toàn đối với phép chiếu song song?
Cắt nhau
Chéo nhau
Song song
Trùng nhau
Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
Hình thang
Hình bình hành
Hình chữ nhật
Hình thoi
Trong mặt phẳng \(\left( \alpha \right)\) cho tứ giác \(ABCD\), điểm \(E \notin \left( \alpha \right)\). Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm \(A,B,C,D,E\)?
\[6\].
\[7\].
\[8\].
\[9\].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tứ diện ABCD. Gọi \(G\) là trọng tâm của tam giác \(ABD,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} Q\) thuộc cạnh \(AB\) sao cho \(AQ = 2{\mkern 1mu} QB,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} P\) là trung điểm của \(AB{\mkern 1mu} .\) Các mệnh đề sau đúng hay sai?
a) \(MN{\rm{//}}\left( {BCD} \right).\) b) \(GQ\)//\(\left( {BCD} \right).\)
c)\(MN\)cắt \(\left( {BCD} \right).\) d) \(Q\) thuộc mặt phẳng \(\left( {CDP} \right).\)
Cho hình hộp \[ABCD.{A_1}{B_1}{C_1}{D_1}.\] Các mệnh đề sau đúng hay sai?
a) \(ABCD\) là hình bình hành.
b) Các đường thẳng \[{A_1}C,\,\,A{C_1},\,\,D{B_1},\,\,{D_1}B\] đồng quy.
c) \(\left( {AD{D_1}{A_1}} \right)\)//\[\left( {BC{C_1}{B_1}} \right).\]
d) \(A{D_1}CB\) là hình chữ nhật.
Cho hình chóp S.ABCD. Gọi \(A'\,,\,\,B',\,\,C',\,\,D'\) lần lượt là trung điểm của các cạnh \(SA\,,\,\,SB,\,\,SC,\,\,SD\) . Các mệnh đề sau đúng hay sai?
a) đường thẳng \(AB\)song song với \(A'B'\,\,\)
b) đường thẳng \(CD\)song song với \(A'B'\,\,\)
c) đường thẳng \(C'D'\)song song với \(A'B'\,\,\)
d) đường thẳng \(SC\)song song với \(A'B'\,\,\)
Xét phép chiếu theo phương d lên mặt phẳng \[(P)\].\[AB\]//\[CF\] và \[AB = DF\]
Gọi \[A',B',C',D',E',F'\] lần lượt là hình chiếu của \[A,B,C,D,E,F\] qua phép chiếu nói trên. Các mệnh đề sau đúng hay sai?
a) \[\frac{{DF}}{{AB}} = \frac{{D'F'}}{{A'B'}} = 1\]
b) \[\frac{{C'D'}}{{C'E'}} = \frac{{CD}}{{CE}}\]
c) \[D'F' = A'B'\]
d) \(CC\prime //DD\prime \)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho \(G\) là trọng tâm tam giác \(ABC,M\) là trung điểm \(BC\) và hình chiếu song song của tam giác \(ABC\) là tam giác \({A^\prime }{B^\prime }{C^\prime }\). Chứng minh rằng hình chiếu \({M^\prime }\) của \(M\) là trung điểm của \({B^\prime }{C^\prime }\) và hình chiếu \({G^\prime }\) của \(G\) cũng là trọng tâm tam giác \({A^\prime }{B^\prime }{C^\prime }\).
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) và một mặt phẳng \((\alpha )\) cắt các mặt của hình hộp theo các giao tuyến \(MN,NP,PQ\), \(QR,RS,SM\) như Hình 18.
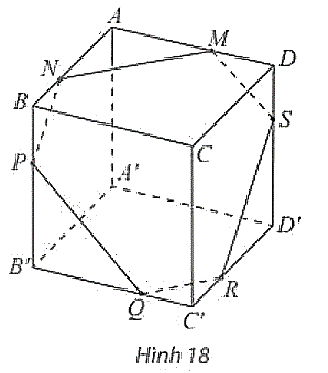
Chứng minh các cặp cạnh đối của lục giác \(MNPQRS\) song song với nhau.
Cho hình thang \(ABCD\) có đáy lớn \(AB\) và \(AB = 2CD\), hình chiếu song song của \(ABCD\) là tứ giác \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Chứng minh rằng \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\) cũng là một hình thang và \({A^\prime }{B^\prime } = 2{C^\prime }{D^\prime }\).
Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.

Mô tả vị trí tương đối của các đường thẳng a,b,c,d,e với mặt phẳng (P) là mặt trước của toà nhà (Hình 19).

Chỉ ra các đường thẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về các đường thẳng song song trong thực tế.