Đề kiểm tra Bài tập cuối chương IV (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho đường thẳng a song song với mặt phẳng \(\left( P \right)\). Mặt phẳng \(\left( Q \right)\)chứa đường thẳng a và cắt mặt phẳng \(\left( P \right)\)theo giao tuyến là đường thẳng \(b\). Vị tri trương đối của hai đường thẳng \(a\)và \(b\) là:
chéo nhau.
cắt nhau.
song song.
trùng nhau.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \(M\) là trung điểm của cạnh \(SD\). Đường thẳng \(SB\) song song với mặt phẳng
\(\left( {CDM} \right)\).
\(\left( {ACM} \right)\).
\(\left( {ADM} \right)\).
\(\left( {ACD} \right)\).
Cho ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) lần lượt tại \(A,B,C\) sao cho \(\frac{{AB}}{{BC}} = \frac{2}{3}\) và đường thẳng \(b\) cắt các mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) lần lượt tại \(A',B',C'\). Tì sô \(\frac{{A'B'}}{{B'C'}}\) bằng
\(\frac{2}{3}\).
\(\frac{1}{2}\).
\(\frac{3}{2}\).
\(\frac{2}{5}\).
Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu?
\[3\].
\[4\].
\[5\].
\[6\].
Cho ABCD là một tứ giác lồi. Hình nào sau đây không thể là thiết diện của hình chóp S.ABCD?
Tam giác.
Tứ giác.
Ngũ giác.
Lục giác.
Cho hình chóp S.ABCD với đáy ABCD là tứ giác lồi. Thiết diện của mặt phẳng \(\left( \alpha \right)\) tuỳ ý với hình chóp không thể là:
Lục giác.
Ngũ giác.
Tứ giác.
Tam giác.
Trong các khẳng định sau, khẳng định nào đúng?
Qua \[2\] điểm phân biệt có duy nhất một mặt phẳng\[.\]
Qua \[3\] điểm phân biệt bất kì có duy nhất một mặt phẳng\[.\]
Qua \[3\] điểm không thẳng hàng có duy nhất một mặt phẳng\[.\]
Qua \[4\] điểm phân biệt bất kì có duy nhất một mặt phẳng\[.\]
Trong không gian, cho \[4\] điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
\[6.\]
\(4.\)
\(3.\)
\(2.\)
Trong mặt phẳng \(\left( \alpha \right)\), cho \[4\] điểm \(A,\;B,\;C,\;D\) trong đó không có \[3\] điểm nào thẳng hàng. Điểm \(S\) không thuộc mặt phẳng \(\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và \[2\] trong \[4\] điểm nói trên?
\(4.\)
\(5.\)
\(6.\)
\(8.\)
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Ba điểm phân biệt\[.\]
Một điểm và một đường thẳng\[.\]
Hai đường thẳng cắt nhau\[.\]
Bốn điểm phân biệt\[.\]
Cho tứ giác \(ABCD\). Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các định của tứ giác \(ABCD\).
\(1.\)
\(2.\)
\(3.\)
\(0.\)
Trong các khẳng định sau, khẳng định nào đúng?
Nếu \[3\] điểm \(A,\;B,\;C\) là 3 điểm chung của 2 mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) thì \(A,\;B,\;C\) thẳng hàng\[.\]
Nếu \(A,\;B,\;C\) thẳng hàng và \(\left( P \right)\), \(\left( Q \right)\) có điểm chung là \(A\) thì \(B,\;C\) cũng là 2 điểm chung của \(\left( P \right)\) và \(\left( Q \right)\)\[.\]
Nếu 3 điểm \(A,\;B,\;C\) là 3 điểm chung của 2 mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) phân biệt thì \(A,\;B,\;C\) không thẳng hàng\[.\]
Nếu \(A,\;B,\;C\) thẳng hàng và \(A,\;B\) là 2 điểm chung của \(\left( P \right)\) và \(\left( Q \right)\) thì \(C\) cũng là điểm chung của \(\left( P \right)\) và \(\left( Q \right)\)\[.\]
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Các mệnh đề sau đúng hay sai?
a) Nếu 3 điểm \(A,\;B,\;C\) là 3 điểm chung của 2 mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) thì \(A,\;B,\;C\) thẳng hàng\[.\]
b) Nếu \(A,\;B,\;C\) thẳng hàng và \(\left( P \right)\), \(\left( Q \right)\) có điểm chung là \(A\) thì \(B,\;C\) cũng là 2 điểm chung của \(\left( P \right)\) và \(\left( Q \right)\)\[.\]
c) Nếu 3 điểm \(A,\;B,\;C\) là 3 điểm chung của 2 mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) phân biệt thì \(A,\;B,\;C\) không thẳng hàng\[.\]
d) Nếu \(A,\;B,\;C\) thẳng hàng và \(A,\;B\) là 2 điểm chung của \(\left( P \right)\) và \(\left( Q \right)\) thì \(C\) cũng là điểm chung của \(\left( P \right)\) và \(\left( Q \right)\)\[.\]
Các mệnh đề sau đúng hay sai?
a) Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thảnh đoạn thẳng.
b) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
c) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi thứ tự của ba điểm đó.
d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.
Cho hình hộp ABCD.EFGH. Các mệnh đề sau đúng hay sai?
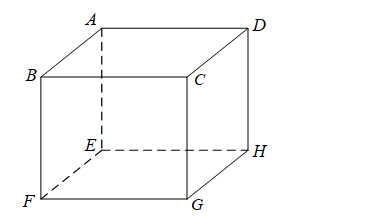
a)\(BG\) và \(HD\) chéo nhau.
b) \(BF\) và \(AD\) chéo nhau.
c) \(AB\) song song với \(HG\).
d)\(CG\) cắt \(HE\).
Cho hình lăng trụ ABC.A'B'C'. Gọi \[H\] là trung điểm của \[A'B'.\] Các mệnh đề sau đúng hay sai?
a) Đường thẳng \[B'C\] song song với mặt phẳng \(\left( {AHC'} \right).\)
b) Đường thẳng \[B'C\] song song với mặt phẳng \(\left( {AA'H} \right).\)
c) Đường thẳng \[B'C\] song song với mặt phẳng \(\left( {HAB} \right).\)
d) Đường thẳng \[B'C\] song song với mặt phẳng \(\left( {HA'C} \right).\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình chóp S.ABCD. Vẽ hình thang ADMS có hai đáy là \(AD\) và \(MS\). Gọi \(d\) là đường thẳng trong không gian đi qua \(S\) và song song với \(AD\). Chứng minh đường thẳng \(d\) nằm trong mặt phẳng \((SAD)\).
Cho đoạn thẳng \[AB\] song song \[\left( P \right)\]. Gọi \[A',B'\] lần lượt là hình chiếu song song của \[A\] và \[B\]trên \[\left( P \right)\] theo phương của đường thẳng \[d\] cho trước. Chứng minh rằng \[A'B' = AB\]. Hỏi rằng nếu ngược lại thì có đúng không ?
Lăng trụ ABC.A'B'C'. \(M,N\) là trung điểm của \(A'C',BC\). Chứng minh \(MN\;{\rm{//}}\;\left( {ABB'A'} \right)\)
Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.

Chỉ ra các mặt phẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về các mặt phẳng song song trong thực tế.

Thước laser phát ra tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng (Hình 41).

Giải thích tại sao các thước kẻ laser lại giúp người thợ xây dựng kẻ được đường thẳng trên tường hoặc sàn nhà.


