Đề kiểm tra Bài tập cuối chương III (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Trong các đẳng thức sau, đẳng thức nào sai?
\(\sin {0^{\rm{o}}} + \cos {0^{\rm{o}}} = 0\).
\(\sin {90^{\rm{o}}} + \cos {90^{\rm{o}}} = 1\).
\(\sin {180^{\rm{o}}} + \cos {180^{\rm{o}}} = - 1\).
\(\sin {60^{\rm{o}}} + \cos {60^{\rm{o}}} = \frac{{\sqrt 3 + 1}}{2}\).
Giá trị của \(E = \sin {36^{\rm{o}}}\cos {6^{\rm{o}}}\sin {126^{\rm{o}}}\cos {84^{\rm{o}}}\) là
\(\frac{1}{2}\).
\(\frac{{\sqrt 3 }}{2}\).
\(1\).
\( - 1\).
Cho tam giác \(ABC\), biết \(a = 24,b = 13,c = 15.\) Tính góc \(A\)?
\({33^0}34'\,.\)
\({117^0}49'\,.\)
\({28^0}37'.\)
\({58^0}24'\,.\)
Tam giác \(ABC\) có \(AB = 9\) cm, \(BC = 15\)cm, \(AC = 12\)cm. Khi đó đường trung tuyến \(AM\) của tam giác có độ dài là
\(10{\rm{ cm}}\).
\(9{\rm{ cm}}\).
\(7,5{\rm{ cm}}\).
\(8{\rm{ cm}}\).
Tổng \({\sin ^2}{2^{\rm{o}}} + {\sin ^2}{4^{\rm{o}}} + {\sin ^2}{6^{\rm{o}}} + ... + {\sin ^2}{84^{\rm{o}}} + {\sin ^2}{86^{\rm{o}}} + {\sin ^2}{88^{\rm{o}}}\) bằng
\(21\).
\(23\).
\(22\).
\(24\).
Cho \(\tan \alpha - \cot \alpha = 3.\) Tính giá trị của biểu thức sau: \(A = {\tan ^2}\alpha + {\cot ^2}\alpha \).
\(A = 12\).
\(A = 11\).
\(A = 13\).
\(A = 5\).
Biểu thức \({\tan ^2}x{\sin ^2}x - {\tan ^2}x + {\sin ^2}x\) có giá trị bằng
\( - 1\).
\(0\).
\(2\).
\(1\).
Gọi \(S = m_a^2 + m_b^2 + m_c^2\) là tổng bình phương độ dài ba trung tuyến của tam giác \(ABC\). Trong các mệnh đề sau mệnh đề nào đúng?
\(S = \frac{3}{4}({a^2} + {b^2} + {c^2})\).
\(S = {a^2} + {b^2} + {c^2}\).
\(S = \frac{3}{2}({a^2} + {b^2} + {c^2})\).
\(S = 3({a^2} + {b^2} + {c^2})\).
Cho tam giác \(ABC\) thoả mãn hệ thức \(b + c = 2a\). Trong các mệnh đề sau, mệnh đề nào đúng?
\[\cos B + \cos C = 2\cos A.\]
\(\sin B + \sin C = 2\sin A.\)
\[\sin B + \sin C = \frac{1}{2}\sin A\].
\(\sin B + \cos C = 2\sin A.\)
Cho tam giác \[ABC\] đều cạnh \[2a\]. Tính bán kính \[R\]của đường tròn ngoại tiếp tam giác \[ABC\].
\[\frac{{2a}}{{\sqrt 3 }}\].
\[\frac{{4a}}{{\sqrt 3 }}\].
\[\frac{{8a}}{{\sqrt 3 }}\].
\[\frac{{6a}}{{\sqrt 3 }}\].
Tam giác với ba cạnh là \(5;12;13\) có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?
\(2.\)
\(2\sqrt 2 .\)
\(2\sqrt 3 .\)
\(3.\)
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, \(\widehat {CAD} = {63^0}\); \(\widehat {CBD} = {48^0}\). Chiều cao h của khối tháp gần với giá trị nào sau đây?
61,4 m.
18,5 m.
60 m.
18 m.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho góc \(\alpha \) thoả mãn \(\sin \alpha = \frac{3}{5}\). Khi đó:
a) \({\sin ^2}\alpha = \frac{9}{{25}}\)
b) \({\cos ^2}\alpha = \frac{{16}}{{25}}\)
c) \[\frac{{\cot \alpha + \tan \alpha }}{{\cot \alpha - \tan \alpha }} = \frac{{25}}{7}\]
d) \(\frac{1}{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }} = \frac{7}{{25}}\)
Cho tam giác \(ABC\) có các cạnh \(a = 3\;cm,b = 4\;cm,c = 5\;cm\). Khi đó:
a) \(p = 12(\;cm)\)
b) \({S_{ABC}} = \sqrt {p(p - a)(p - b)(p - c)} \)
c) \({S_{ABC}} = 6\left( {\;c{m^2}} \right).\)
d) \[R = 3,5(\;cm)\]
Cho tam giác \(ABC\) biết các cạnh \(a = 52,1\;cm,b = 85\;cm,c = 54\;cm\). Khi đó:
a) \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)
b) \(A \approx {32^0}\)
c)
d)
Cho \(\Delta ABC\) có \(AB = 3,AC = 4\;A\), diện tích \(S = 3\sqrt 3 \). Khi đó:
a) \(B{C^2} = A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A\)
b) \(\sin A = - \frac{{\sqrt 3 }}{2}\)
c) \(\cos A = \frac{1}{2}\)
d) \(\cos A = - \frac{1}{2}\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tính giá trị biểu thức sau:
Tính giá trị của biểu thức \(P = \frac{{2\sin \alpha - \sqrt 2 \cos \alpha }}{{4\sin \alpha + 3\sqrt 2 \cos \alpha }}\) biết \(\cot \alpha = - \sqrt 2 \).
Cho hai góc \(\alpha \) và \(\beta \) với . Tính giá trị của biểu thức
\(P = \cos \alpha \cos \beta - \sin \beta \sin \alpha {\rm{. }}\)
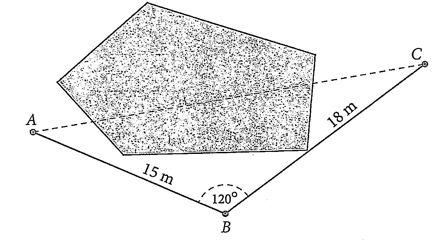
Để kéo dây điện từ cột điện vào nhà phải qua một cái ao, anh Nam không thể đo độ dài dây điện cần mua trực tiếp được nên đã làm như sau: Lấy một điểm \(B\) như trong hình, người ta đo được độ dài từ \(B\) đến \(A\) (nhà) là \(15\;m\), từ \(B\) đến \(C\) (cột điện) là \(18\;m\) và . Hãy tính độ dài dây điện nối từ nhà ra đến cột điện.
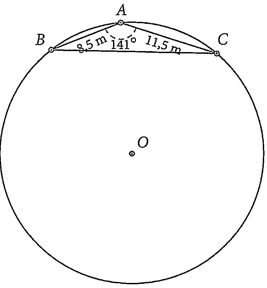
Để đo đường kính một hồ hình tròn, người ta làm như sau: Lấy ba điểm \(A,B,C\) như hình vẽ, sao cho \(AB = 8,5m;AC = 11,5m;\widehat {BAC} = 141^\circ \). Hãy tính đường kính của hồ nước đó.
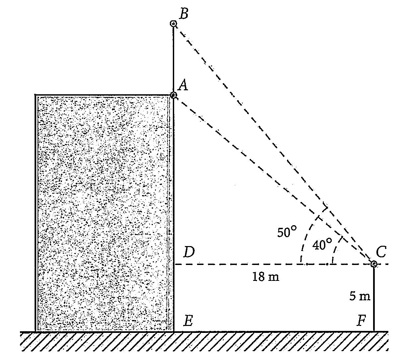
Để đo chiều cao của một cột cờ trên đỉnh một toà nhà anh Bắc đã làm như sau: Anh đứng trên một đài quan sát có tầm quan sát cao \(5\;m\) so với mặt đất, khi quan sát anh đo được góc quan sát chân cột là 400 và góc quan sát đỉnh cột là 500, khoảng cách từ chân toà nhà đến vị trí quan sát là \(18\;m\). Tính chiều cao cột cờ và chiều cao của toà nhà.