Đề kiểm tra Bài tập cuối chương III (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Tuổi đời của \(16\) công nhân trong xưởng sản xuất được thống kê trong bảng sau

Tìm số trung bình \(\overline x \) của mẫu số liệu trên.
\(28\).
\(27,75\).
\(27,875\).
\(27\).
Điểm số của \(100\) học sinh tham dự kỳ thi học sinh giỏi toán ở tỉnh \(A\) (thang điểm là \(20\)) được thống kê theo bảng sau:
Trung bình cộng của bảng số liệu trên là
\(15\).
\(15,50\).
\(16\).
\(15,23\).
Điều tra về số tiền mua đồ dùng học tập trong một tháng của 40 học sinh, ta có mẫu số liệu như sau (đơn vị: nghìn đồng):

\Số trung bình của mẫu số liệu là
\(22,5\).
\(25\).
\(25,5\).
\(27\).
Tuổi đời của \(16\)công nhân trong xưởng sản xuất được thống kê trong bảng sau
Số trung bình \(\overline x \)của mẫu số liệu trên là
\(28\).
\(27,75\).
\(27,875\).
\(27\).
Ba nhóm học sinh gồm 10 người, 15 người, 25 người. Cân nặng trung bình của mỗi nhóm lần lượt là 50kg, 38kg, 40kg. Khối lượng trung bình của ba nhóm học sinh đó là
\(26\)kg.
\(41,4\)kg.
\(42,4\)kg.
\(37\)kg.
Kết quả điểm kiểm tra 45 phút môn Hóa Học của 100 em học sinh được trình bày ở bảng sau:
Số trung bình cộng của bảng phân bố tần số nói trên là
\(6,82\).
\(4\).
\(6,5\).
\(7,22\).
Cho bảng phân bố tần số sau: khối lượng \(20\) học sinh lớp \(10A\)
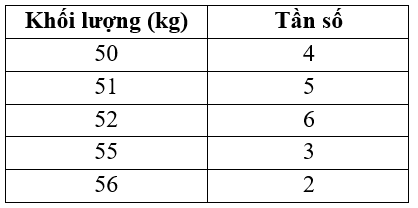
Số trung bình cộng \(\overline x \) của bảng số liệu đã cho là
\(\overline x = 53\).
\(\overline x = 52,8\).
\(\overline x = 52,2\).
\(\overline x = 52\).
Điểm thi học kì của một học sinh như sau: \[4;\,6;\,2;\,7;\,3;\,5;\,9;\,8;\,7;\,10;\,9\]. Số trung bình và số trung vị lần lượt là
\(6,22\)và \(7\).
\(7\) và \(6\).
\(6,36\) và \(7\).
\(6\) và \(6\).
Một nhóm \(10\) học sinh tham gia một kỳ thi. Số điểm thi của \(10\) học sinh đó được sắp xếp từ thấp đến cao như sau (thang điểm 10): \(0;1;2;4;4;5;7;8;8;9\). Tìm số trung vị của mẫu số liệu.
\(5\).
\(5,5\).
\(4,5\).
\(4\).
Cho bảng số liệu ghi lại điểm của\(40\)học sinh trong bài kiểm tra một tiết môn Toán
Số trung vị là
\(6,5\).
\(6\).
\(5\).
\(7\).
Thống kê điểm kiểm tra \(15'\) môn Toán của một lớp 10 của trường THPT M.V. Lômônôxốp được ghi lại như sau:
Số trung vị của mẫu số liệu trên là
\(8\).
\(6\).
\(7\).
\(9\).
Cho bảng số liệu điểm bài kiểm tra môn toán của 20 học sinh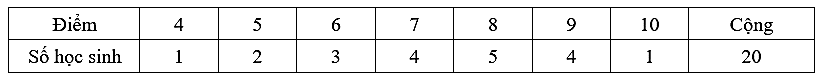
Tìm số trung vị của bảng số liệu trên.
\(8\).
\(7,5\).
\(7,3\).
\(7\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Thâm niên giảng dạy của một số giáo viên trường THPT được ghi lại ở bảng sau:
Thâm niên (Số năm) | \([1;5)\) | \([5;10)\) | \([10;15)\) | \([15;20)\) | \([20;25)\) |
Số giáo viên | 4 | 12 | 16 | 8 | 3 |
a)Cỡ mẫu của mẫu số liệu bằng \(50\).
b) Số trung bình của mẫu ghép nhóm là \(11,84\)
c) Nhóm chứa mốt của mẫu số liệu trên là nhóm \([10;15)\).
d) Mốt của mẫu số liệu ghép nhóm bằng \(11,74.{\rm{ }}\)
Số câu trả lời đúng một bài thi trắc nghiệm môn Sinh học gồm 50 câu của lớp \(11\;A\) ở một trường THPT như sau:
Số câu đúng | \([14;21)\) | \([21;28)\) | \([28;35)\) | \([35;42)\) | \([42;49)\) |
Số học sinh | 4 | 8 | 25 | 6 | 7 |
a) Giá trị đại diện của nhóm \([14;21)\) là: 17,5
b) Giá trị đại diện của nhóm \([21;28)\) là: 24,5
c) Giá trị đại diện của nhóm \([42;49)\) là: 45,5
d) Số câu đúng trung bình là \(32,26.\)
Giả sử kết quả khảo sát hai khu vực \(A\) và \(B\) về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:
Tuổi kết hôn | \([19;22)\) | \([22;25)\) | \([25;28)\) | \([28;31)\) | \([31;34)\) |
Số phụ nữ khu vực \(A\) | 10 | 27 | 31 | 25 | 7 |
Số phụ nữ khu vực \(B\) | 47 | 40 | 11 | 2 | 0 |
Các mệnh đề sau đúng hay sai?
a) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: \(15\) (tuổi)
b) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: \(12\)(tuổi)
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm ứng với khu vực A là: \(\frac{{61}}{3}\) (tuổi)
d) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn
Kết quả đo chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau:
Chiều cao \((m)\) | \([8,4;8,6)\) | \([8,6;8,8)\) | \([8,8;9,0)\) | \([9,0;9,2)\) | \([9,2;9,4)\) |
Số cây | 5 | 12 | 25 | 44 | 14 |
Các mệnh đề sau đúng hay sai?
a) Khoảng biên thiên của mẫu số liệu ghép nhóm: \(1(m)\)
b) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 10,5\)
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = 2,06\)
d) Trong 100 cây keo trên có 1 cây cao \(8,4\;m\). Thì chiều cao của cây keo này là giá trị ngoại lệ
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau:

Tìm mốt của mẫu số liệu. Giải thích ý nghĩa của giá trị nhận được.
Sau khi đã thu thập dữ liệu về lượng nước sinh hoạt trong một tháng của từng hộ gia đình ở hai khu vực dân cư, bác Vinh muốn đánh giá xem hộ gia đình ở khu vực nào dùng hết nhiều nước sinh hoạt hơn. Theo bạn bác Vinh nên làm thế nào?
Thời gian chạy 100 mét (đơn vị: giây) của các bạn học sinh ở hai nhóm và được ghi lại ở bảng sau:

Nhóm nào có thành tích chạy tốt hơn?
Chỉ số BMI (đo bằng \({\rm{w}}/{h^2}\), trong đó w là cân nặng đơn vị là kilôgam, h là chiều cao đơn vị là mét) của các học sinh trong một tổ được cho như sau:
Một người có chỉ số BMI nhỏ hơn 18,5 được xem là thiếu cân; từ 18,5 đến dưới 23 là có cân nặng lí tưởng so với chiều cao; từ 23 trở lên là thừa cân. Hãy lập mẫu số liệu ghép nhóm cho mẫu số liệu trên để biểu diễn tình trạng cân nặng so với chiều cao của các học sinh trong tổ.
Trong một cuộc đua Marathon được tổ chức ở thành phố A người ta thống kê lại được như sau

Hãy ước lượng số trung bình và tứ phân vị của mẫu số liệu ghép nhóm trên.
Số sản phẩm một công nhân làm được trong một ngày được cho như sau:
\[\begin{array}{*{20}{l}}\begin{array}{l}18 & 25 & 39 & 12 & 54 & 27 & 46 & 25 & 19 & 8 & 36 & 22\\20 & 19 & 17 & 44 & 5 & 18 & 23 & 28 & 25 & 34 & 46 & 27\end{array}\end{array}\]
Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sáu nhóm có độ dài bằng nhau.


