10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho hình hộp \[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Chọn đẳng thức sai?
\(\overrightarrow {BC} - \overrightarrow {{B_1}{C_1}} = \overrightarrow {{B_1}{A_1}} - \overrightarrow {BA} \).
\(\overrightarrow {AD} + \overrightarrow {{D_1}{C_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow {DC} \).
\(\overrightarrow {BC} + \overrightarrow {BA} + \overrightarrow {B{B_1}} = \overrightarrow {B{D_1}} \).
\(\overrightarrow {BA} + \overrightarrow {D{D_1}} + \overrightarrow {B{D_1}} = \overrightarrow {BC} \).
Cho hình hộp \(ABCD.A'B'C'D'\).
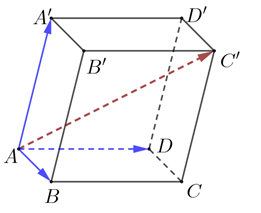
Vectơ \(\overrightarrow {AC'} \) là kết quả của phép tính tổng nào sau đây?
\(\overrightarrow {AA'} + \overrightarrow {AD} + \overrightarrow {CD} \).
\(\overrightarrow {AA'} + \overrightarrow {B'C'} \).
\(\overrightarrow {AA'} + \overrightarrow {AD} + \overrightarrow {AB} \).
\(\overrightarrow {AA'} + \overrightarrow {A'B} + \overrightarrow {B'C'} \).
Cho hình lập phương \(ABCD.A'B'C'D'\). Mệnh đề nào sau đây sai?
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\).
\(\overrightarrow {AB} = \overrightarrow {CD} \).
Cho tứ diện\(ABCD\), gọi \(I\), \(J\) lần lượt là trung điểm của \(AB\) và \(CD\). Đẳng thức nào sai?
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\].
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\].
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {AD} + \overrightarrow {BD} } \right)\].
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\].
Cho tứ diện \(ABCD\). Mệnh đề nào dưới đây là mệnh đề đúng?
\(\overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {DA} - \overrightarrow {DC} \).
\(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BD} - \overrightarrow {BC} \).
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {DB} - \overrightarrow {DC} \).
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CD} + \overrightarrow {BC} \).
Cho tứ diện \[ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[AB\] và \[CD\], \[G\] là trung điểm của \[IJ\]. Cho các đẳng thức sau, đẳng thức nào đúng?
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {{\rm{IJ}}} \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow {JI} \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = - 2\overrightarrow {JI} \].
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Góc giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {BD} \).
\(150^\circ \).
\(120^\circ \).
\[30^\circ \].
\[60^\circ \].
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và mặt bên SAB là tam giác đều. Tính góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {BS} \).
\(150^\circ \).
\(120^\circ \).
\[90^\circ \].
\[60^\circ \].
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Xác định góc \(\alpha \) giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\)
\(\alpha = {180^{\rm{o}}}\) .
\(\alpha = {0^{\rm{o}}}\) .
\(\alpha = {90^{\rm{o}}}\) .
\(\alpha = {45^{\rm{o}}}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Mặt bên ASB là tam giác vuông cân tại \(S\) và có cạnh \(AB = a\). Tính \(\overrightarrow {DC} .\overrightarrow {AS} \).
\(\frac{a}{{\sqrt 2 }}\) .
\({a^2}\) .
\(\frac{{{a^2}}}{2}\) .
\(\frac{{{a^2}}}{{\sqrt 2 }}\).
