10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Đồ thị được cho trong hình vẽ dưới đây là của hàm số nào?

\[y = {\rm{ }}{x^4} - 2{x^2}\].
\[y = {x^{\rm{3}}} - 3x - 1\].
\[y = - {x^{\rm{3}}} + 3x\].
\[y = {x^3} - 3x\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
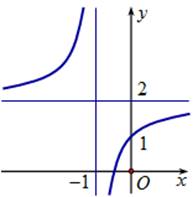
\(y = \frac{{2x - 1}}{{x + 1}}\).
\(y = \frac{{2x + 1}}{{x + 1}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{2x + 1}}{{x - 1}}\).
Bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó.

\(y = \frac{{2x - 3}}{{x + 1}}\).
\(y = \frac{{2x + 3}}{{x + 1}}\).
\(y = \frac{{ - 2x - 3}}{{x + 1}}\).
\(y = \frac{{ - x + 1}}{{x - 2}}\).
Đồ thị hàm số \(y = {x^3} - 3x + 2\) là hình nào trong 4 hình dưới đây?
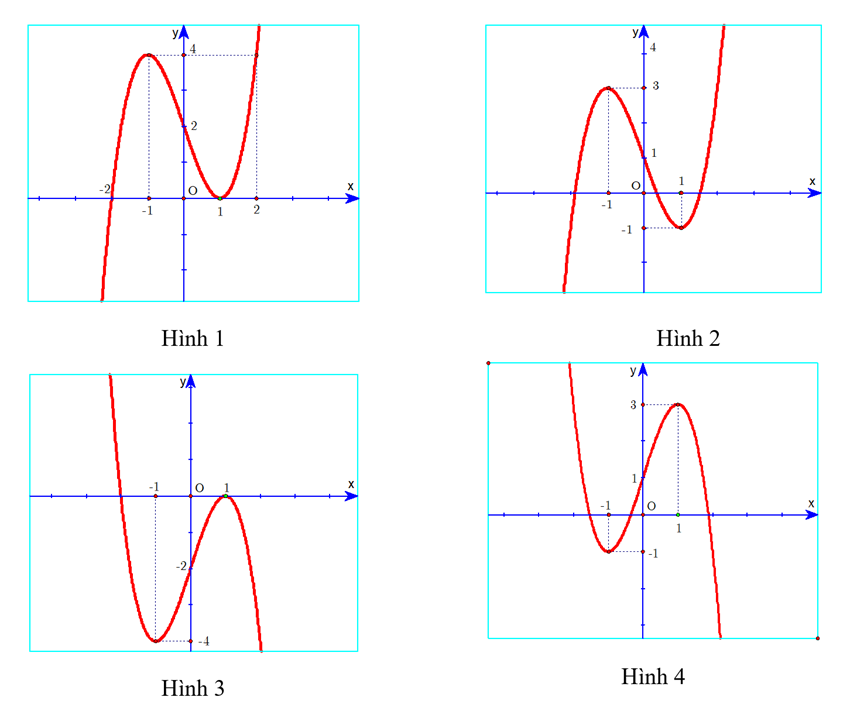
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\] có đồ thị như hình vẽ bên dưới.
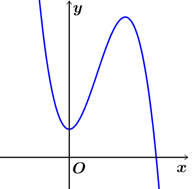
Mệnh đề nào dưới đây đúng?
\[a < 0,b > 0,c > 0,d > 0\].
\[a < 0,b < 0,c = 0,d > 0\].
\[a > 0,b < 0,c > 0,d > 0\].
\[a < 0,b > 0,c = 0,d > 0\].
Cho hàm số \(y = \frac{{x + b}}{{cx + d}}\) có đồ thị như hình vẽ bên
Xác định dấu của các hệ số \(b\), \(c\), \(d\).
\(b < 0,\,c > 0,\,d > 0\).
\(b < 0,\,c > 0,\,d < 0\).
\(b > 0,\,c < 0,\,d > 0\).
\(b > 0,\,c < 0,\,d < 0\).
Đường cong trong hình là đồ thị của hàm số nào dưới đây?

\(y = \frac{{ - {x^2} + 1}}{x}\).
\(y = \frac{{ - 2x + 1}}{{2x + 2}}\).
\(y = \frac{{{x^2} - x + 1}}{{x - 1}}\).
\(y = {x^3} - 3{x^2}\).
Bảng biến thiên sau là của một trong bốn hàm số sau.
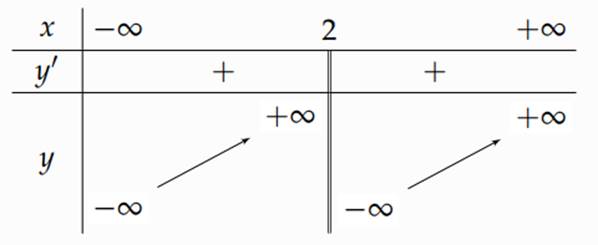
Hỏi đó là hàm số nào?
\(y = \frac{{{x^2} - 3}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\).
\(y = \frac{{{x^2} - x}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\).
Đườngcongtronghìnhbênlàđồthịcủahàmsố nào?

\(y = \frac{{{x^2} - x - 1}}{{x + 2}}\).
\(y = \frac{{{x^2} - x - 1}}{{x - 2}}\).
\(y = \frac{{{x^2} - 2x - 1}}{{x - 2}}\).
\(y = \frac{{{x^2} - x + 1}}{{x - 2}}\).
Đồ thị của hàm số nào dưới đây có dnagj như đường cong trong hình sau.

\(y = \frac{{2x + 1}}{{x + 1}}\).
\(y = {x^3} - 3x - 1\).
\(y = \frac{{2x - 1}}{{x + 1}}\).
\(y = \frac{{2{x^2} + 3x + 2}}{{x + 1}}\).
