10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Một chất điểm chuyển động theo quy luật \(s\left( t \right) = {t^2} - \frac{1}{6}{t^3}\left( {\rm{m}} \right).\) Tìm thời điểm \(t\) (giây) mà tại đó vận tốc \(v\left( {{\rm{m/s}}} \right)\) của chuyển động đạt giá trị lớn nhất.
\(t = 2\).
\(t = 0,5\).
\(t = 2,5\).
\(t = 1\).
Một vật chuyển động theo quy luật \(s = - 2{t^3} + 24{t^2} + 9t - 3\) với \(t\) là khoảng thời gian tính từ lúc bắt đầu chuyển động và \(s\) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
289 \(\left( {{\rm{m/s}}} \right)\).
105 \(\left( {{\rm{m/s}}} \right)\).
111 \(\left( {{\rm{m/s}}} \right)\).
487 \(\left( {{\rm{m/s}}} \right)\).
Một chất điểm chuyển động có phương trình \(S = {t^3} - 3{t^2} - 9t + 2\), trong đó t được tính bằng giây và S được tính bằng mét. Gia tốc tại thời điểm vận tốc bị triệt tiêu là:
\[ - 9{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[9{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[ - 12{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[12{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng \(10{\rm{ }}{{\rm{m}}^{\rm{3}}}\). Thùng tôn là hình hộp chữ nhật có chiều dài đáy bằng hai lần chiều rộng và không có nắp. Trên thị trường giá tôn làm đáy thùng là \(75000/{{\rm{m}}^{\rm{2}}}\) và giá tôn làm thành xung quanh thùng là \(55000/{{\rm{m}}^{\rm{2}}}\). Tính chi phí thấp nhất để làm thùng đựng gạo. (Làm tròn đến hàng đơn vị)
\(1418000\) đồng.
\(1403000\) đồng.
\(1402000\) đồng.
\(1417000\) đồng.
Một người dự định làm một bể chứa nước hình trụ bằng inox có nắp đậy với thể tích \(1\) (m3). Chi phí mỗi m2 đáy là \(600\) nghìn đồng, mỗi m2 nắp là \(200\) nghìn đồng và mỗi m2 mặt bên là \(400\) nghìn đồng. Hỏi người đó làm bán kính bể là bao nhiêu để chi phí làm bể ít nhất?
\(\sqrt[3]{{2\pi }}\).
\(\sqrt[3]{{\frac{1}{2}}}\).
\(\sqrt[3]{{\frac{1}{{2\pi }}}}\).
\(\sqrt[3]{{\frac{1}{\pi }}}\).
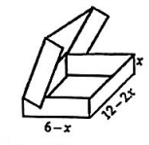
Một hộp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên của hộp được rải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi \(x = {x_0}\) là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị \({V_0}\) bằng
64 (đvtt).
\(\frac{{64}}{3}\,\)(đvtt).
\(16\,\)(đvtt).
48 (đvtt).
Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2000000 đồng mỗi tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ 100000 đồng mỗi tháng thì có thêm 2 căn hộ bị bỏ trống. Muốn có thu nhập cao nhất, công ty đó phải cho thuê với giá mỗi căn hộ là bao nhiêu?
2250000.
2350000.
2450000.
2550000.
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa được là 60 hành khách một chuyến. Nếu một chuyến chở được m hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận mỗi chuyến xe là lớn nhất.?
30.
40.
50.
60
Một loại vi khuẩn được tiêm một loại thuốc kích thích sự sinh sản. Sau t phút, số vi khuẩn được xác định theo công thức \[N(t) = 1000 + 30{t^2} - {t^3}\,(0 \le t \le 30)\]. Hỏi sau bao giây thì số vi khuẩn lớn nhất?
\(20\).
\(10\).
\(1200\).
\(1100\).
Sau khi phát hiện dịch bệnh, các chuyên gia y tế ước tính số người bị nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f\left( t \right) = 1 + 18{t^2} - \frac{1}{3}{t^3}\), \(t = \left( {0,1,2,...,30} \right)\). Nếu coi \(f\left( t \right)\) là hàm số xác định trên đoạn thì \(f'\left( t \right)\) được xem là tốc độ truyền bệnh tại thời điểm \(t\). Xác định ngày mà tốc độ truyền bệnh lớn nhất.
\(18\).
\(30\).
\(15\).
\(36\).
