Đề cương ôn tập cuối kì 1 Toán 8 Chân trời sáng tạo cấu trúc mới (Tự luận) có đáp án - Phần 2
4 câu hỏi
Cho hình chữ nhật \(ABCD\), kẻ \(AH,CK\) vuông góc với \(BD\) \(\left( {H,\,\,K \in BD} \right)\).
a) Chứng minh \(DH = BK\).
b) Chứng minh tứ giác \(AHCK\) là hình bình hành.
c) Gọi \(E\) là điểm đối xứng với \(A\) qua \(H\). Chứng minh \(DECB\) là hình thang cân.
Cho ba số thực \(x,y,z \ne 0\) và \(x + y + z = 0\). Tính giá trị của biểu thức
\(T = \frac{{xy}}{{{x^2} + {y^2} - {z^2}}} + \frac{{yz}}{{{y^2} + {z^2} - {x^2}}} + \frac{{xz}}{{{z^2} + {x^2} - {y^2}}}\).
Bác Bảy có một trang trại lớn để trồng rau và chăn nuôi gia cầm. Bác dự định mua một tấm lưới thép B40 để rào bao quanh khu vực nuôi gia cầm của trang trại với thiết kế có dạng hình chữ nhật \(ABCD\)(như hình mô tả ở bên). Biết rằng, bác Bảy không rào xung quanh khu vực nhà kho và vị trí nhà kho cố định. Với số tiền của mình, bác Bảy chỉ mua được tấm lưới có chiều dài \(500\,\,{\rm{m}}\). Hỏi bác Bảy sẽ dựng rào chắn như thế nào để diện tích khu nuôi gia cầm là lớn nhất?
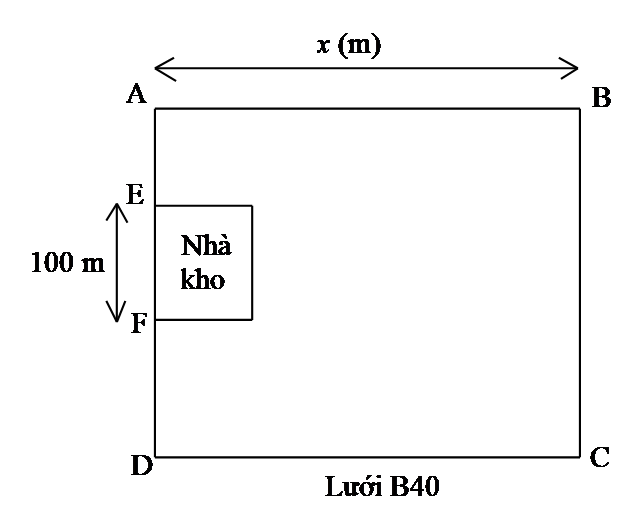
Một tấm bìa cứng hình chữ nhật có chiều dài là \({\rm{50 cm}}\) và chiều rộng là \({\rm{30 cm}}\). Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh \(x{\rm{\;(cm)}}\) và xếp phần còn lại thành một hình hộp không nắp. Tìm \(x\) để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.