Dạng 5. Phiếu bài tập tự luyện có đáp án

Cho $\Delta ABC$ cân tại A, có AMlà đường trung tuyến ứng với BC. CMR: cạnh AB đối xứng với AC qua AM.

Cho tam giác nhọn ABC, trực tâm H. Gọi K là điểm đối xứng với H qua BC. Tìm hệ thức liên hệ giữa số đo các góc BAC, BKC.

Cho $△$ABC, gọi m là đường trung trực của BC. Vẽ D đối xứng với A qua ma) Tìm các đoạn thẳng đối xứng với AB, AC qua m .

b) Tứ giác ABCD là hình gì?

Cho hình thang vuông $ABC\text{D }(\widehat{A}=\widehat{D}={90}^0)$. Gọi K là điểm đối xứng với C qua AD. CMR: $\widehat{AIB}=\widehat{CI\text{D}}$.

Cho $\Delta ABC$, gọi d là đường phân giác ngoài ở đỉnh A. Trên đường thẳng d lấy điểm $M (M\ne A)$. CMR: $BA+AC<BM+MC$.

Cho $\Delta ABC$ vuông tại A. Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng với M qua AB, AC. Chứng minh A là trung điểm của EF.

Cho tam giác ABC cân tại B

a) Tìm trục đối xứng của tam giác đó

b) Gọi trục đối xứng đó là d. Kể trên hình đối xứng qua d của: đỉnh A, đỉnh B, đỉnh C, cạnh AB, cạnh AC

Cho điểm A nằm trong góc nhọn xOy. Dựng điểm B thuộc tia Ox, điểm C  thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.

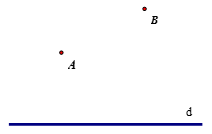
Cho đường thẳng d và hai điểm A, B (như hình vẽ). Tìm vị trí điểm C trên d để chu vi tam giác ABC nhỏ nhất.

Cho tam giác ABC có các đường phân giác BD, CE cắt nhau ở O. Qua A vẽ các đường vuông góc với BD và với CE, chúng cắt BC theo thứ tự ở N và M. Gọi H là chân đường vuông góc kẻ từ O đến BC. Chứng minh rằng:

a) M đối xứng với A qua CE, N đối xứng với A qua BD;

b) M đối xứng với N qua OH.

Cho tam giác ABC vuông ở A, lấy D là điểm bất kì thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, F là điểm đối xứng với D qua AC.

a) Chứng minh rằng A là trung điểm của EF.

b) Điểm D ở vị trí nào trên cạnh BC thì EF có độ dài ngắn nhất.

Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là điểm đối xứng của điểm H qua AB và AC. Chứng minh rằng:

a) A là trung điểm của đoạn DE

b) Tứ giác BDEC là hình thang vuông.

c) Cho BH = 2cm, CH = 8cm. Tính AH và chu vi hình thang BDEC.

Cho tam giác ABC có $=70°$, B và C là các góc nhọn. M là một điểm thuộc cạnh BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đỗi ứng với M qua AC. Gọi I, K là giao điểm của DE với AB, AC.

a) Tính các góc của tam giác ADE.

b) Chứng minh rằng MA là tia phân giác của góc IMK.

c) Điểm M ở vị trí nào trên cạnh BC thì DE có độ dài ngắn nhất?

Cho hai điểm A và B cùng nằm trên nửa mặt phẳng bờ là đường thẳng d. Tìm trên d một điểm C sao cho tổng độ dài CA + CB là ngắn nhất.