24 câu hỏi
Cho hàm số \(y = f(x)\) liên tục trên \([a;b](a,b \in \mathbb{R},a < b).\) Gọi \(S\) là diện tích của hình phẳng giới hạn bởi các đường \({\rm{y}} = {\rm{f}}({\rm{x}}),{\rm{y}} = 0,{\rm{x}} = {\rm{a}},{\rm{x}} = {\rm{b}}.\) Phát biểu nào sau đây là đúng?
\(S = \int_b^a f (x)dx.\)
\(S = \int_b^a | f(x)|dx.\)
\(S = \left| {\int_a^b f (x)dx} \right|.\)
\(S = \int_a^b | f(x)|dx.\)
Cho các hàm số \(y = f(x),y = g(x)\) liên tục trên \([a;b](a,b \in \mathbb{R},a < b).\) Gọi \(S\) là diện tích của hình phẳng giới hạn bởi các đường \(y = f(x),y = g(x),x = a\), \({\rm{x}} = {\rm{b}}.\) Phát biểu nào sau đây là đúng?
\(S = \left| {\int_a^b {(f(} x) - g(x))dx} \right|.\)
\(S = \int_b^a \mid (f(x) - g(x))dx.\)
\(S = \int_a^b \mid (f(x) - g(x))dx.\)
\(S = \int_b^a {(f(} x) - g(x))dx.\)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị cắt trục Ox tại đúng hai điểm phân biệt \({\rm{a}},{\rm{b}}.\) Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox. Nếu \(f(x) \ge 0\forall x \in [a;b]\) thì
\(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}}){\rm{dx}} = {\rm{S}}.\)
\(\int_a^b f (x)dx = (a - b)S.\)
\(\int_a^b f (x)dx = - S.\)
\(\int_a^b f (x)dx = (b - a)S.\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị cắt trục Ox tại đúng hai điểm phân biệt \({\rm{a}},{\rm{b}}.\) Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox. Nếu \({\rm{f}}({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{a}};{\rm{b}}]\) thì
\(\int_a^b f (x)dx = S.\)
\(\int_a^b f (x)dx = (a - b)S.\)
\(\int_a^b f (x)dx = - S.\)
\(\int_a^b f (x)dx = (b - a)S.\)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{c}};{\rm{b}}].\) Nếu \({\rm{f}}({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}],{\rm{f}}({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}}){\rm{dx}}\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({{\rm{S}}_1} - {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{c}};{\rm{b}}].\) Nếu \({\rm{f}}({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}],{\rm{f}}({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}})\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({{\rm{S}}_1} - {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{c}};{\rm{b}}].\) Nếu \({\rm{f}}({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}],{\rm{f}}({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}})\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({{\rm{S}}_1} - {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox tương ứng với \({\rm{x}} \in [{\rm{c}};{\rm{b}}].\) Nếu \({\rm{f}}({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}],{\rm{f}}({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}})\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({{\rm{S}}_1} - {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \(y = f(x)\) có đạo hàm là hàm liên tục trên \(\mathbb{R}\) và có đồ thị \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \(x \in [{\rm{c}};{\rm{b}}].\) Nếu \({{\rm{f}}^\prime }({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}]\), \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(f(b) - f(a)\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({S_1} - {S_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \(y = f(x)\) có đạo hàm là hàm liên tục trên \(\mathbb{R}\) và có đồ thị \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \({\rm{x}} \in [{\rm{c}};{\rm{b}}].\) Nếu \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{f}}^\prime }({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(f(b) - f(a)\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({{\rm{S}}_1} - {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \(y = f(x)\) có đạo hàm là hàm liên tục trên \(\mathbb{R}\) và có đồ thị \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \({\rm{x}} \in [{\rm{c}};{\rm{b}}].\) Nếu \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}]\), \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(f(b) - f(a)\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({{\rm{S}}_1} - {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \(y = f(x)\) có đạo hàm là hàm liên tục trên \(\mathbb{R}\) và có đồ thị \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) cắt trục Ox tại đúng ba điểm phân biệt \({\rm{a}},{\rm{b}},{\rm{c}}({\rm{a}} < {\rm{c}} < {\rm{b}}).\) Gọi \({{\rm{S}}_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{S}}_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \({{\rm{f}}^\prime }({\rm{x}})\) và trục Ox tương ứng với \({\rm{x}} \in [{\rm{c}};{\rm{b}}].\) Nếu \({{\rm{f}}^\prime }({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{a}};{\rm{c}}],{{\rm{f}}^\prime }({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{c}};{\rm{b}}]\) thì giá trị của \(f(b) - f(a)\) bằng
\({{\rm{S}}_1} + {{\rm{S}}_2}.\)
\({{\rm{S}}_1} - {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} + {{\rm{S}}_2}.\)
\( - {{\rm{S}}_1} - {{\rm{S}}_2}.\)
Cho hàm số \(y = f(x)\) thoả mãn hàm \(y = {f^\prime }(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị của biểu thức \({\rm{f}}(4) - {\rm{f}}( - 4)\) bằng
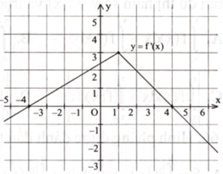
12.
3.
24.
6.
Cho hàm số \(y = f(x)\) thoả mãn hàm \(y = {f^\prime }(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị của biểu thức \({\rm{f}}(6) - {\rm{f}}(1)\) bằng
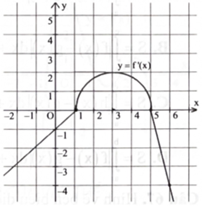
\(4\pi - 2.\)
\(2\pi + 2.\)
\(2\pi - 4.\)
\(2\pi - 2.\)
Hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = - {{\rm{x}}^2} + 2{\rm{x}}\) và trục Ox có diện tích là
\(\frac{4}{3}.\)
\(\frac{2}{3}.\)
\(\frac{8}{3}.\)
\(\frac{{20}}{3}.\)
Hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {{\rm{x}}^2}\) và đường thẳng \({\rm{y}} = 2{\rm{x}} + 3\) có diện tích là
\(\frac{{49}}{3}.\)
\(\frac{{29}}{3}.\)
\(\frac{{22}}{3}.\)
\(\frac{{32}}{3}.\)
Hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {{\rm{e}}^{\rm{x}}}\) và các đường thẳng \({\rm{y}} = 1,{\rm{x}} = - 1\) có diện tích là
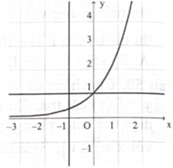
\(\frac{1}{{\rm{e}}}.\)
\(1 - \frac{1}{{\rm{e}}}.\)
\({\rm{e}} - 1.\)
e.
Hình vẽ bên biểu diễn trục hoành cắt đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) tại ba điểm có hoành độ \({{\rm{x}}_1},{{\rm{x}}_2},{{\rm{x}}_3}\)\(\left( {{x_1} < {x_2} < {x_3}} \right).\) Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\) và trục hoành là
![Hình vẽ bên biểu diễn trục hoành cắt đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) tại ba điểm có hoành độ \({{\rm{x}}_1},{{\rm{x}}_2},{{\rm{x}}_3}\) \(\left( {{x_1} < {x_2} < {x_3}} \right).\) Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\) và trục hoành là A. \(\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx.\) B. \(\int_{{x_1}}^{{x_2}} f (x)dx - \int_{{x_2}}^{{x_3}} f (x)dx.\) C. \[\left| {\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx} \right|.\] D. \(\left| {\int_{{{\rm{x}}_1}}^{{{\rm{x}}_3}} {\rm{f}} ({\rm{x}}){\rm{dx}}} \right|.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid3-1727016691.png)
\(\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx.\)
\(\int_{{x_1}}^{{x_2}} f (x)dx - \int_{{x_2}}^{{x_3}} f (x)dx.\)
\[\left| {\int_{{x_1}}^{{x_2}} f (x)dx + \int_{{x_2}}^{{x_3}} f (x)dx} \right|.\]
\(\left| {\int_{{{\rm{x}}_1}}^{{{\rm{x}}_3}} {\rm{f}} ({\rm{x}}){\rm{dx}}} \right|.\)
Hình phẳng được đánh dấu trong hình vẽ sau có diện tích là
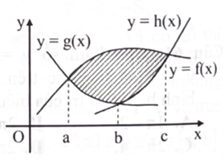
\(S = \int_a^b | h(x) - g(x)|dx + \int_b^c | h(x) - f(x)|dx.\)
\(S = \int_a^c | f(x) - g(x)|dx + \int_b^c | f(x) - h(x)|dx.\)
\(S = \int_a^c | h(x) - g(x)|dx + \int_b^c | h(x) - f(x)|dx.\)
\(S = \int_a^b | f(x) - g(x)|dx + \int_b^c | f(x) - h(x)|dx.\)
Hình vẽ bên biểu diễn đường thẳng\({\rm{y}} = {\rm{m}}\)cắt đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) tại ba điểm có hoành độ \({{\rm{x}}_1}\), \({{\rm{x}}_2},{{\rm{x}}_3}\left( {{{\rm{x}}_1} < {{\rm{x}}_2} < {{\rm{x}}_3}} \right).\) Diện tích phần hình phẳng giới hạn bởi hai đường trên là
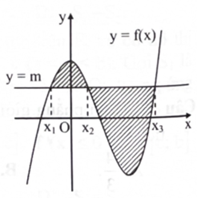
\(\int_{{x_1}}^{{x_2}} {(f(} x) - m)dx + \int_{{x_2}}^{{x_2}} {(f(} x) - m)dx.\)
\(\int_{{x_1}}^{{x_2}} {(f(} x) - m)dx - \int_{{x_2}}^{{x_2}} {(f(} x) - m)dx.\)
\(\int_{{x_1}}^{{x_2}} {(m - f(} x))dx + \int_{{x_2}}^{{x_2}} {(m - f(} x))dx.\)
\(\left| {\int_{{x_1}}^{{x_1}} {(f(} x) - m)dx} \right|.\)
Diện tích hình phẳng giới hạn bởi các đường \({\rm{y}} = \sqrt {\rm{x}} ,{\rm{y}} = 2 - {\rm{x}}\) và trục Ox được tính bởi công thức
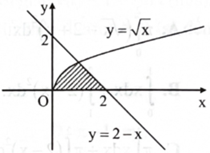
\(\int_0^2 {(\sqrt x - 2 + x)} dx.\)
\(\int_0^2 {(2 - x - \sqrt x )} dx.\)
\(\int_0^1 {\sqrt x } dx + \int_1^2 {(2 - x)} dx.\)
\(\int_0^2 {\sqrt x } dx + \int_0^2 {(2 - x)} dx.\)
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {2^{\rm{x}}}\) và các đường thẳng \({\rm{y}} = 2;{\rm{x}} = - 1;{\rm{x}} = 2\) có giá trị bằng
\(\int_1^2 {\left( {{2^x} - 2} \right)} dx.\)
\(\int_{ - 1}^2 {\left( {{2^x} - 2} \right)} dx.\)
\(\int_{ - 1}^2 {\left( {2 - {2^x}} \right)} dx.\)
\(\int_{ - 1}^1 {\left( {2 - {2^x}} \right)} dx + \int_1^2 {\left( {{2^x} - 2} \right)} dx.\)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) có đồ thị cắt trục Ox tại đúng 4 điểm phân biệt (hình bên). Biết rằng \(\int_{ - 1}^1 {\rm{f}} ({\rm{x}}){\rm{dx}} = 21\), \(\int_1^2 f (x)dx = - 2,\int_2^3 f (x)dx = 3.\) Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và trục Ox bằng
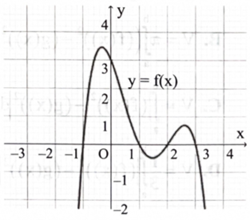
22.
20.
16.
26.
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) có đồ thị cắt trục Ox tại đúng 4 điểm phân biệt (hình bên). Biết rằng \(\int_{ - 1}^1 {\rm{f}} ({\rm{x}}){\rm{dx}} = 21\), \(\int_1^2 f (x)dx = - 2,\int_2^3 f (x)dx = 3.\) Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và trục Ox bằng
22.
20.
16.
26.
Gợi ý cho bạn
Xem tất cảCÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
CÂU TRẮC NGHIỆM ĐÚNG SAI
DẠNG 5. MỘT SỐ ỨNG DỤNG CỦA TÍCH PHÂN TRONG VẬT LÍ
DẠNG 2. KHÁI NIỆM TÍCH PHÂN, TÍNH CHẤT CỦA TÍCH PHÂN