11 câu hỏi
Cho \({\rm{a}},{\rm{b}} \in \mathbb{R}\), hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có một nguyên hàm là hàm số \({\rm{y}} = {\rm{F}}({\rm{x}}).\) Phát biểu nào sau đây là đúng?
\(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}}){\rm{dx}} = {\rm{F}}({\rm{b}}) - {\rm{F}}({\rm{a}}).\)
\(\int_a^b f (x)dx = F(a) - F(b).\)
\(\int_a^b f (x)dx = F(b) + F(a).\)
\(\int_{\rm{a}}^{\rm{b}} {\rm{f}} ({\rm{x}}){\rm{dx}} = {\rm{F}}({\rm{b}}){\rm{F}}({\rm{a}}).\)
Cho \({\rm{a}},{\rm{b}} \in \mathbb{R}\), các hàm số \({\rm{y}} = {\rm{f}}({\rm{x}}),{\rm{y}} = {\rm{g}}({\rm{x}})\) liên tục trên \(\mathbb{R}.\) Biểu thức \(\int_a^b {\left[ {f(x) + g(x)} \right]} dx\) bằng
\(\int_a^b f (x)dx - \int_a^b g (x)dx.\)
\(\int_a^b f (x)dx + \int_a^b g (x)dx.\)
\(\int_a^b f (x)dx + \int_b^a g (x)dx.\)
\(\int_a^b g (x)dx - \int_a^b f (x)dx.\)
Cho \(b \in [a;c];a,b,c \in \mathbb{R}\), hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}.\) Biểu thức \(\int_a^c f (x)dx\) bằng
\(\int_a^b f (x)dx + \int_c^b f (x)dx.\)
\(\int_a^b f (x)dx + \int_b^c f (x)dx.\)
\(\int_b^a f (x)dx + \int_b^c f (x)dx.\)
\(\int_b^c f (x)dx + \int_c^b f (x)dx.\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đạo hàm là hàm liên tục trên \(\mathbb{R}.\forall {\rm{a}},{\rm{b}} \in \mathbb{R}\), giá trị của biểu thức \(\int_a^b {{f^\prime }} (x)dx\) bằng
\(f(a) - f(b).\)
\(f(b) - f(a).\)
\(f(a) + f(b).\)
\(f(a) \cdot f(b).\)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R},\int_3^5 f (x)dx = 2.\) Biểu thức \(\int_5^3 f (x)dx\) bằng
2.
\(\frac{1}{2}.\)
-2.
\(\frac{{ - 1}}{2}.\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R},\int_6^7 {\rm{f}} ({\rm{x}}){\rm{dx}} = 4.\) Biểu thức \(\int_6^7 2 0{\rm{f}}({\rm{x}}){\rm{dx}}\) bằng
80.
24.
16.
5.
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R},\int_1^2 f (x)dx = 3,\int_1^3 f (x)dx = 5.\) Biểu thức \(\int_2^3 {\rm{f}} ({\rm{x}}){\rm{dx}}\) bằng
3.
8.
2.
15.
Nếu \(\int_3^{\rm{m}} {{x^2}} dx = 4\) thì
\({\rm{m}} = \sqrt {39} .\)
\({\rm{m}} = \pm \sqrt[3]{{39}}.\)
\({\rm{m}} = - \sqrt[3]{{39}}.\)
\({\rm{m}} = \sqrt[3]{{39}}.\)
Nếu \({\rm{b}} - {\rm{a}} = 3\) thì biểu thức \(\int_{\rm{a}}^{\rm{b}} {{{\rm{x}}^2}} {\rm{dx}}\) có giá trị bằng
\(3 - {\rm{ab}}.\)
\(9 - 3ab.\)
\(9 + 3ab.\)
\(3 + ab.\)
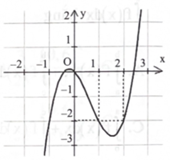
Cho hàm số \(y = f(x)\) có đồ thị như hình bên và đạo hàm \({{\rm{f}}^\prime }({\rm{x}})\) liên tục trên \(\mathbb{R}.\) Giá trị của biểu thức \(\int_1^2 {{{\rm{f}}^\prime }} ({\rm{x}}){\rm{dx}}\) bằng
2.
4.
1.
0.
Cho \(0 < {\rm{a}} < 1 < {\rm{b}}.\) Tích phân \(I = \int_{\rm{a}}^{\rm{b}} {\left| {{{\rm{x}}^2} - {\rm{x}}} \right|} d{\rm{x}}\) bằng
\( - \int_a^1 {\left( {{x^2} - x} \right)} dx + \int_1^b {\left( {{x^2} - x} \right)} dx.\)
\(\int_a^1 {\left( {{x^2} - x} \right)} dx - \int_1^b {\left( {{x^2} - x} \right)} dx.\)
\(\int_a^1 {\left( {{x^2} - x} \right)} dx + \int_1^b {\left( {{x^2} - x} \right)} dx.\)
\( - \int_a^1 {\left( {{x^2} - x} \right)} dx - \int_1^b {\left( {{x^2} - x} \right)} dx.\)
Gợi ý cho bạn
Xem tất cảCÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
CÂU TRẮC NGHIỆM ĐÚNG SAI
DẠNG 5. MỘT SỐ ỨNG DỤNG CỦA TÍCH PHÂN TRONG VẬT LÍ