Dạng 2: Tìm giới hạn của dãy số dựa vào các định lý và các giới hạn cơ bản có đáp án
84 câu hỏi
Cho dãy số (un) với 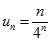 và
và 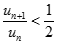 . Chọn giá trị đúng của
. Chọn giá trị đúng của 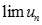 trong các số sau:
trong các số sau:
0
1
Kết quả đúng của 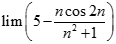 là:
là:
4
5
-4
Giá trị của 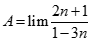 bằng:
bằng:
+∞
-∞
1
Giá trị của 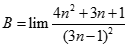 bằng:
bằng:
+∞
-∞
0
Kết quả đúng của 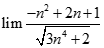 là
là
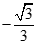
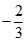
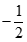
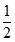
Giới hạn dãy số 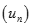 với
với 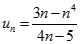 là:
là:
-∞
+∞
0
Chọn kết quả đúng của 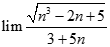 :
:
5
-∞
+∞
Giá trị của 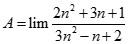 bằng:
bằng:
+∞
-∞
1
Giá trị của 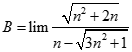 bằng:
bằng:
+∞
-∞
0
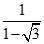
Giá trị của 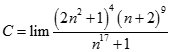 bằng:
bằng:
+∞
-∞
16
1
Giá trị của 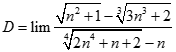 bằng:
bằng:
+∞
-∞
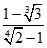
1
Giá trị của 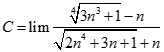 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 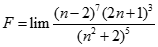 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 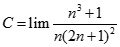 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 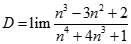 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 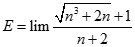 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 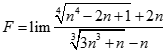 bằng:
bằng:
+∞
-∞
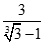
1
Cho dãy số 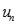 với
với 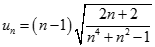 . Chọn kết quả đúng của
. Chọn kết quả đúng của 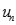 là:
là:
-∞
0
1
+∞
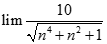 bằng:
bằng:
+∞
10
0
-∞
Tính giới hạn: 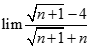
1
0
-1
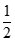
Tính giới hạn: 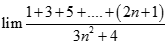
0
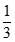
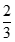
1
Chọn kết quả đúng của 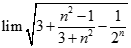 .
.
4
3
2
Giá trị của 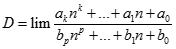 (Trong đó k, p là các số nguyên dương;
(Trong đó k, p là các số nguyên dương; 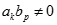 ).
).
+∞
-∞
Đáp án khác
1
Kết quả đúng của 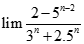 là:
là:
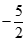
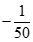
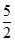
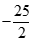
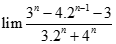 bằng:
bằng:
+∞
-∞
0
1
Giá trị của 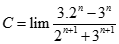 bằng:
bằng:
+∞
-∞
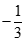
1
Giá trị đúng của 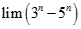 là:
là:
-∞
+∞
2
-2
Giá trị của 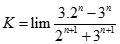 bằng:
bằng:
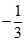
-∞
2
1
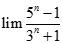 bằng:
bằng:
+∞
1
0
-∞
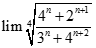 bằng:
bằng:
0
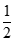
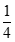
+∞
Giá trị của. 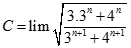 bằng:
bằng:
+∞
0
1
Cho các số thực a,b thỏa 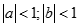 . Tìm giới hạn
. Tìm giới hạn 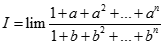 .
.
+∞
-∞
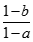
1
Tính giới hạn của dãy số 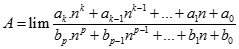 với
với 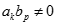 .
.
+∞
-∞
Đáp án khác
1
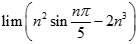 bằng:
bằng:
+∞
0
-2
-∞
Giá trị của. 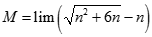 bằng:
bằng:
-∞
-∞
3
1
Giá trị của 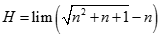 bằng:
bằng:
+∞
-∞
1
Giá trị của 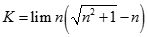 bằng:
bằng:
+∞
-∞
1
Giá trị đúng của 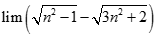 là:
là:
+∞
-∞
0
1
Giá trị của 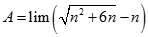 bằng:
bằng:
+∞
-∞
3
1
Giá trị của 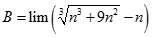 bằng:
bằng:
+∞
-∞
0
3
Giá trị của 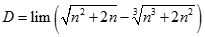 bằng:
bằng:
+∞
-∞
1
Giá trị của 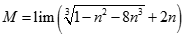 bằng:
bằng:
-∞
0
1
Giá trị của 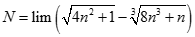 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 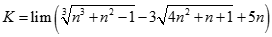 bằng:
bằng:
+∞
-∞
1
Giá trị của. 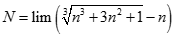 bằng:
bằng:
+∞
-∞
0
1
Giá trị đúng của ![Giá trị đúng của lim [ căn bậc hai n (căn bậc hai n + 1 - căn bậc hai n - 1)] là: A. -1 B. 0 C. 1 D. dương vô cùng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid25-1669818935.png) là:
là:
-1
0
1
+∞
Giá trị của 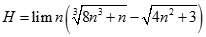 bằng:
bằng:
+∞
-∞
1
Giá trị của 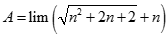 bằng:
bằng:
+∞
-∞
2
1
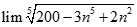 bằng:
bằng:
0
1
+∞
-∞
Giá trị của. 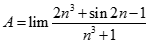 bằng:
bằng:
+∞
-∞
2
1
Giá trị của. 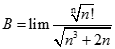 bằng:
bằng:
+∞
0
0
1
Giá trị của. 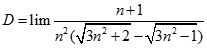 bằng:
bằng:
+∞
-∞
1
Giá trị của. 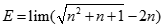 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 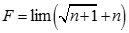 bằng:
bằng:
+∞
-∞
0
1
Giá trị của. 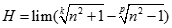 bằng:
bằng:
+∞
-∞
Đáp án khác
1
Tính giới hạn của dãy số 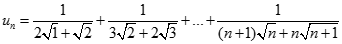 :
:
+∞
-∞
0
1
Tính giới hạn của dãy số 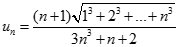 :
:
+∞
-∞
1
Tính giới hạn của dãy số 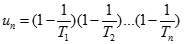 trong đó
trong đó 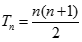
+∞
-∞
1
Tính giới hạn của dãy số 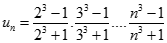
+∞
-∞
1
Tính giới hạn của dãy số 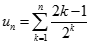
+∞
-∞
3
1
Tính giới hạn của dãy số 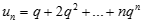 với
với 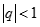
+∞
-∞
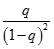
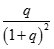
Tính giới hạn của dãy số 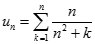
+∞
-∞
3
1
Tính giới hạn của dãy số 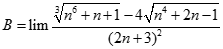
+∞
-∞
3
-
Tính giới hạn của dãy số 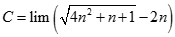
+∞
-∞
3
Tính giới hạn của dãy số 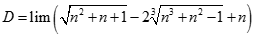
+∞
-∞
1
Cho dãy số 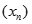 xác định bởi
xác định bởi 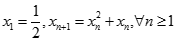
Đặt 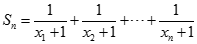 . Tính
. Tính 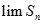
+∞
-∞
2
1
Cho dãy 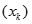 được xác định như sau:
được xác định như sau: 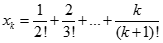
Tìm 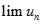 với
với 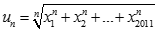 .
.
+∞
-∞
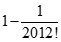
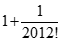
Cho dãy số 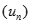 được xác định bởi:
được xác định bởi: 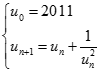 . Tìm
. Tìm 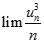 .
.
+∞
-∞
3
1
Cho dãy x > 0 xác định như sau: 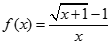 . Tìm
. Tìm  .
.
+∞
-∞
2010
1
Tìm 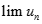 biết
biết 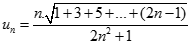
+∞
-∞
1
Tìm 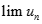 biết
biết 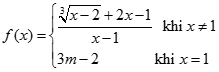
+∞
-∞
2
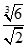
Tìm 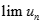 biết
biết 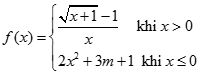
+∞
-∞
2
1
Tìm 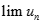 biết
biết 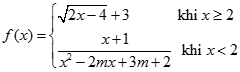 trong đó
trong đó 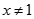 .
.
+∞
-∞
1
Tìm 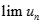 biết
biết 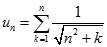
+∞
-∞
3
1
Tìm 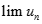 biết
biết 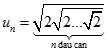
+∞
-∞
2
1
Cho dãy số 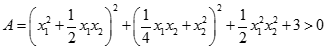 được xác định như sau
được xác định như sau 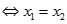 .
.
Đặt 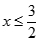 . Tìm
. Tìm 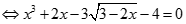 .
.
+∞
-∞
1
Cho 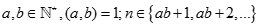 . Kí hiệu
. Kí hiệu 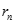 là số cặp số
là số cặp số 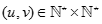
sao cho 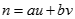 . Tìm
. Tìm 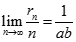
+∞
-∞
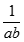
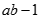
Cho dãy số có giới hạn (un) xác định bởi 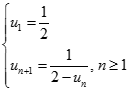 . Tìm kết quả đúng của
. Tìm kết quả đúng của 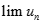 .
.
0
1
-1
Tìm giá trị đúng của 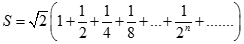
+ 1
2
Tính giới hạn: ![Tính giới hạn: lim [ 1/1.2 + 1/2.3 + ... + 1/n(n+ 1)] A. 0 B. 1 C. 3/2 D. không giới hạn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid3-1669825453.png)
0
1
Không có giới hạn.
Tính giới hạn: ![Tính giới hạn: lim [1/1.3 + 1/3.5 + ... + 1/n(2n+1)] A. 1 B. 0 C. 2/3 D. 2 . Chọn B Đặt A = 1/1.3 + 1/3.5 + ... + 1/n(2n+1) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid6-1669825586.png)
1
0
2
Tính giới hạn: ![Tính giới hạn: lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] A. 3/4 B. 1 C. 0 D. 2/3 Chọn A lim [1/1.3 + 1/2.4 + .... + 1/n(n+2)] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid9-1669825717.png)
1
0
Tính giới hạn: ![Tính giới hạn: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] A. 11/18 B.2 C. 1 D. 3/2 Chọn A Cách 1: lim [1/1.4 + 1/2.5 + ... + 1/n(n+3)] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid12-1669825838.png) .
.
2
1
Tính giới hạn: ![Tính giới hạn: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] A. 1 B. 1/2 C. 1/4 D. 3/2 Chọn B. Cách 1: lim [(1-1/2^2)( 1-1/3^2) ... (1 - 1/n^2)] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/11/blobid15-1669825983.png) .
.
1






