Bộ 7 Đề thi Toán 11 Học kì 2 có đáp án (Đề 6)
23 câu hỏi
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 5x + 1}}{{1 + 3x - {x^2}}}\)bằng:
+¥
2
−2
1
Đạo hàm của hàm số y = cosx là:
y' = sinx
y' = −cotx
y' = −sinx
y' = tanx
\(\mathop {\lim }\limits_{x \to 2} \left( { - 3{x^2} + 6x + 1} \right)\) bằng:
−¥
1
−3
3
Cho hàm số f(x) = 2x3 – 8. Giá trị f'(−2) bằng:
24
16
−24
4
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC) và SA = a. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
90°
60°
30°
45°
\(\mathop {\lim }\limits_{x \to + \infty } \left( { - {x^4} + 5{x^2} - 3} \right)\) bằng
+¥
−¥
−1
1
Hàm số y = \(\frac{{3x - 1}}{{x + 1}}\) có đạo hàm là y' = \(\frac{m}{{{{(x + 1)}^2}}}\), giá trị của P = 2m – 1 là:
7
4
−9
3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Trong các khẳng định sau, khẳng định nào sai?
SA ^ (ABC)
BC ^ (SAB)
BD ^ (SAC)
CD ^ (SBC)
Phương trình tiếp tuyến của đồ thị hàm số y = x4 – 3x2 + 1 tại điểm M(1;−1) là:
y = 2x – 3
y = -x + 1
y = -2x + 1
y = -2x + 3
\(\mathop {\lim }\limits_{x \to {{( - 2)}^ - }} \frac{{5 - 3x}}{{x + 2}}\) bằng:
+¥
11
5
−¥
Phát biểu nào sau đây là đúng?
(sin3x)' = 3.cos3x
(sin3x)' = −3.cos3x
(sin3x)' = 3.sin3x
(sin3x)' = cos3x
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và có SA = SC, SB = SD. Trong các khẳng định sau, khẳng định nào đúng?
SA ^ (ABCD)
SO ^ (ABCD)
SC ^ (ABCD)
SB ^ (ABCD)
Cho hàm số . Hàm số đã cho liên tục tại x = 2 khi a bằng:
\( - \frac{2}{3}\)
2
\( - \frac{4}{3}\)
\(\frac{2}{3}\)
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {4{x^2} - 4x + 7} - 2x} \right)\) bằng:
−¥
2
−1
+¥
Đường thẳng y = ax + b tiếp xúc với đồ thị hàm số y = x3 – 3x – 1 tại điểm có hoành độ bằng 2, giá trị của a + b bằng:
26
−8
−9
10
Cho chuyển động thẳng xác định bởi phương trình S = 2t4 – 9t2 + 3, trong đó t được tính bằng giây và S được tính bằng mét. Vận tốc của chuyển động tại thời điểm t = 2 (giây) là:
64 (m/s)
12(m/s)
100(m/s)
28(m/s)
Xét tính liên tục của hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\frac{{2{x^2} - x - 6}}{{x - 2}}\,\,khi\,x \ne 2}\\{5x - 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 2}\end{array}} \right.\) tại x0 = 2.
Chứng minh rằng phương trình 2x4 – 3x3 – 5 = 0 có ít nhất một nghiệm.
Cho hàm số y = f(x) = \(\frac{1}{3}\)x3 + 2x2 – \(\frac{2}{3}\) có đồ thị (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến song song với đường thẳng d: y = −4x + 2022.
Giải bất phương trình f'(x) > −1, biết rằng f(x) = (x2 – 2x)(x – 3).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với cạnh AB = \(a\sqrt 2 \), SA vuông góc với mặt phẳng đáy và SA = 3a.
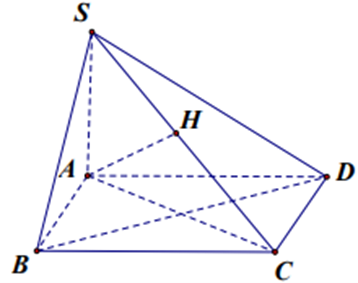
Chứng minh CD ^ (SAD).
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh , SA ⊥ (ABCD) và SA = 3a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Gọi H là hình chiếu vuông góc của A trên SC. Chứng minh AH ^ BD và tính độ dài đoạn AH.








