12 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Điều kiện xác định của phương trình \(\frac{1}{{x - 3}} - 3 = \frac{2}{{\left( {x - 3} \right)\left( {x + 4} \right)}}\) là
\[x \ne 4;{\rm{ }}x \ne - 3\].
\[x \ne 3;{\rm{ }}x \ne - 4\].
\[x \ne 3;{\rm{ }}x \ne 6\].
\[x \ne 0;{\rm{ }}x \ne - 3\].
Tổng các nghiệm của phương trình \(\left( {\frac{1}{3}x - 3} \right)\left( {x + 8} \right) = 0\) là
\(5\).
\(1\).
\( - 5\).
\( - 1\).
Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn?
\[2x - 3y = 5.\]
\[0x + 2y = 4.\]
\[2x - 0y = 3.\]
\[0x - 0y = 6.\]
Nghiệm tổng quát của phương trình \(3x + y = 6\) là
\(\left( {x;\,\, - 3x - 6} \right)\) với \(x \in \mathbb{R}\) tùy ý.
\(\left( { - 3y + 6;\,\,y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
\[\left( {x;\,\, - 3x + 6} \right)\] với \[x \in \mathbb{R}\] tùy ý.
\(\left( { - 3y - 6;\,\,y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9\end{array} \right.?\)
\(\left( {1;\,\,1} \right).\)
\(\left( {1;\,\, - 1} \right).\)
\(\left( { - 21;\,\,15} \right).\)
\(\left( {21;\,\, - 15} \right).\)
Cho hình vẽ dưới đây:
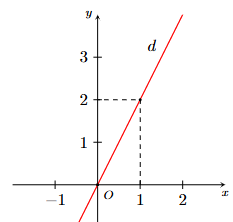
Đường thẳng \[d\] biểu diễn nghiệm của phương trình nào?
\[y = 2x.\]
\[y = - 2x.\]
\[y = 2x + 1.\]
\[y = - 2x + 1.\]
Bất đẳng thức \(m \le - 8\) có thể được phát biểu là
\(m\) lớn hơn âm 8.
\(m\) không nhỏ hơn âm 8.
\(m\) nhỏ hơn âm 8.
\(m\) không lớn hơn âm 8.
Với ba số \(a,b\) và \(c < 0\), các khẳng định sau khẳng định nào đúng?
Nếu \[a > b\] thì \(ac > bc.\)
Nếu \(a > b\) thì \(\frac{a}{c} > \frac{b}{c}.\)
Nếu \(a > b\) thì \(ac < bc.\)
Nếu \(a > b\) thì \(a + c < b + c.\)
Tam giác \[ABC\] vuông tại \[A\]. Khẳng định nào sau đây đúng?
\[AC = AB.\tan B.\]
\[AB = BC.\tan B.\]
\[AC = BC.\tan B.\]
\[AB = AC.\tan B.\]
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,\,\,AC = b,\,\,AB = c\). Hệ thức nào sau đây là sai?
\(b = a \cdot \sin B = a \cdot \cos C\).
\(a = c \cdot \tan B = c \cdot \cot C\).
\({a^2} = {b^2} + {c^2}.\)
\(c = a \cdot \sin C = a \cdot \cos B\).
Cho góc \(\alpha \) thỏa mãn \(0^\circ < \alpha < 90^\circ \). Biết \(\tan \alpha = \frac{4}{3}\). Giá trị của \(\cot \left( {90^\circ - \alpha } \right)\) bằng
\(\frac{3}{4}\).
\(\frac{4}{3}\).
\(\frac{5}{3}\).
\(\frac{5}{4}\).
Cho hình bình hành \[ABCD\]có \[AC \bot AD\] và \(AD = 3,5\,;\,\,\widehat D = 50^\circ \). Hỏi diện tích của hình bình hành là bao nhiêu? (Kết quả làm tròn đến hàng phần mười)
14.
\[14,6.\]
\[14,5.\]
\[14,9.\]
