12 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Điều kiện xác định của phương trình \(\frac{1}{{x + 2}} + 1 = \frac{2}{{x - 1}}\) là
\[x \ne 1;{\rm{ }}x \ne - 3\].
\[x \ne 2;{\rm{ }}x \ne 1\].
\[x \ne - 3;{\rm{ }}x \ne --2\].
\(x \ne - 2;{\rm{ }}x \ne 1.\)
Phương trình \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0\) có nghiệm là
\[x = - 9\,;\,\,x = 4\]
\[x = 4.\]
\[x = - 9.\]
\[x = 9\,;\,\,x = 4.\]
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
\[5x - 3z = 6\].
\(5x - 8y = 0.\)
\[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Phương trình \(0x + 7y = 14\) có nghiệm tổng quát là
\(\left( {x;\,\,2} \right)\) với \(x \in \mathbb{R}\).
\(\left( {2;\,\,y} \right)\) với \(y \in \mathbb{R}\).
\(\left( {x;\,\,0} \right)\) với \(x \in \mathbb{R}\).
\(\left( {0;\,\,y} \right)\) với \(y \in \mathbb{R}\).
Giá trị của \(a\) và \(b\) để cặp số \[\left( { - 2;\,\,3} \right)\] là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ax + y = 5}\\{3x + by = 0}\end{array}} \right.\) là
\(\left( {a;\,\,b} \right) = \left( { - 3;\,\,3} \right)\).
\(\left( {a;\,\,b} \right) = \left( { - 2;\,\,1} \right)\).
\(\left( {a;\,\,b} \right) = \left( {2;\,\, - 4} \right)\).
\(\left( {a;\,\,b} \right) = \left( { - 1;\,\,2} \right)\).
Hình nào dưới đây biểu diễn tất cả các nghiệm của phương trình \[2x + y = 3?\]
A. 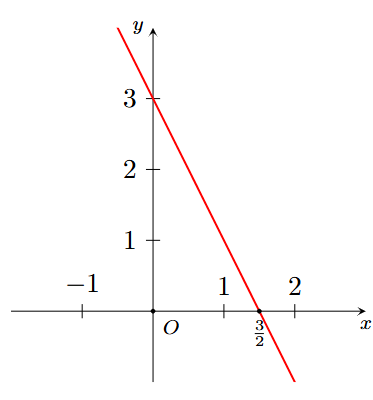
B. 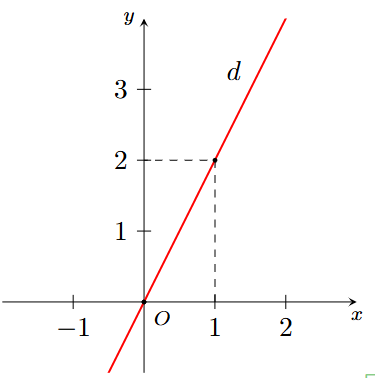
C. 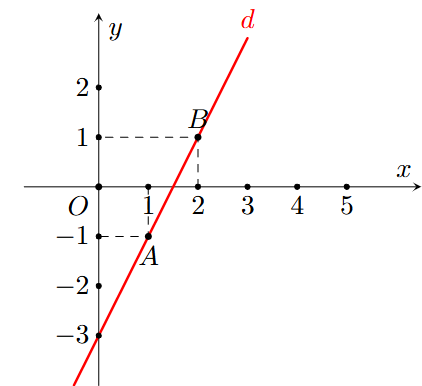
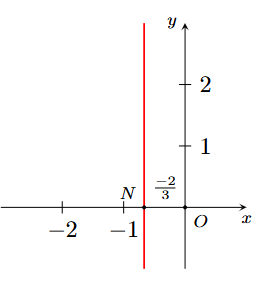
Phát biểu “\(a\) không nhỏ hơn \(b\)” được biểu diễn bằng bất đẳng thức nào dưới đây?
\(a < b.\)
\(a \ge b.\)
\(a \le b.\)
\(a > b.\)
Nghiệm \[x = 5\] thỏa mãn bất phương trình nào dưới đây?
\[5 + 7x \le 11.\]
\[2,5x - 6 > 9 + 4x.\]
\[5 + 7x \ge 15.\]
\[3 - 0,2x > 13.\]
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó, \(\sin \widehat {ABC}\) bằng:
\(\frac{{AC}}{{BC}}.\)
\(\frac{{BC}}{{AC}}.\)
\(\frac{{AB}}{{BC}}.\)
\(\frac{{AB}}{{AC}}.\)
Cho tam giác \(ABC\) vuông tại \(A\). Hệ thức nào sau đây là sai?
\(BC = \frac{{AC}}{{\sin B}}.\)
\(BC = \frac{{AB}}{{\sin C}}.\)
\(BC = \frac{{AC}}{{\cos C}}.\)
\(AB = \frac{{AC}}{{\tan C}}.\)
Cho \(\alpha \) và \(\beta \) là hai góc nhọn bất kì thỏa mãn \[\alpha + \beta = 90^\circ \] và \[\sin \alpha = 0,5.\] Khẳng định nào sau đây là đúng?
\[\sin \beta = 0,5.\]
\[\cos \beta = 0,5.\]
\[\tan \beta = 0,5.\]
\[\cot \beta = 0,5.\]
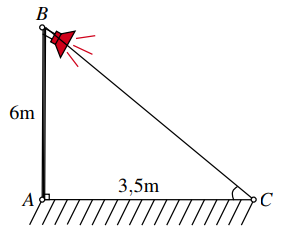
Một cột đèn \(AB\) cao 6 m có bóng in trên mặt đất là \(AC\) dài \(3,5\;{\rm{m}}\). Góc (làm tròn đến phút) mà tia sáng từ đèn \(B\) tạo với mặt đất là
\(58^\circ 45\prime \).
\(59^\circ 50\prime \).
\(59^\circ 45\prime \).
\(59^\circ 4\prime \).
