Bộ 5 đề thi giữa kì 1 Toán 6 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 2
21 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Phát biểu “\[a\] không thuộc \(A\)” được kí hiệu là
\[a \in A.\]
\[a \notin A.\]
\[A \in a.\]
\[A \notin a.\]
Số tự nhiên lớn nhất có bốn chữ số khác nhau là
\(9\;999\).
\(6\;789\).
\(9\;876\).
\(9\;087\).
Biểu thức nào sau đây sử dụng đúng dấu ngoặc?
\[200:\left( {2 \cdot \left[ {20 - \left\{ {\left. {10 + 5} \right\}} \right.} \right]} \right).\]
\(200:\left\{ {\left. {2 \cdot \left( {20 - \left[ {10 + 5} \right]} \right)} \right\}} \right..\)
\(200:\left\{ {\left. {2 \cdot \left[ {20 - \left( {10 + 5} \right)} \right]} \right\}} \right..\)
\(200:\left[ {2 \cdot \left\{ {\left. {20 - \left( {10 + 5} \right)} \right\}} \right.} \right].\)
Kết quả của phép tính \({a^m} \cdot {a^n}\) là
\({a^{m\,\, \cdot \,\,n}}.\)
\({a^{m + n}}.\)
\({a^{m - n}}.\)
\({\left( {{a^m}} \right)^n}.\)
Cho \(x\) là số tự nhiên thỏa mãn \({10^7} < x < {10^8}.\) Số \(x\) có
9 chữ số.
8 chữ số.
7 chữ số.
10 chữ số.
Cụm từ thích hợp điền vào chỗ trống trong phát biểu “Trong phép chia có dư, số dư bao giờ cũng … số chia” là
nhỏ hơn.
lớn hơn.
nhỏ hơn hoặc bằng.
lớn hơn hoặc bằng.
Các chữ số \(x;y\) thoả mãn \(\overline {1x2y} \) chia hết cho cả \(2;\,\,5\) và \(9\) là
\(x = 5;\,\,y = 1\).
\(x = 1;\,\,y = 5\).
\(x = 0;\,\,y = 6\).
\(x = 6;\,\,y = 0\).
Khẳng định nào dưới đây là sai?
Số \[2\] là số nguyên tố nhỏ nhất.
Các số chẵn khác \[2\] là hợp số.
Tổng của hainguyên tố lớn hơn \[2\] luôn là hợp số.
Tổng của hai hợp số luôn là một hợp số.
Cho các biển báo giao thông sau:

Khẳng định nào sau đây là sai?
Hình 1 là biển báo dừng lại có dạng hình lục giác đều.
Hình 2 là biển báo bắt đầu nơi đỗ xe có dạng hình vuông.
Hình 3 là biển báo nguy hiểm có dạng hình tam giác đều.
Hình 4 là biển báo cấm đi ngược chiều có dạng hình tròn.
Hình thoi không có tính chất nào dưới đây?
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Các cạnh đối song song.
Hai đường chéo bằng nhau.
Hai đường chéo vuông góc với nhau.
Cho hình lục giác đều \(MNPQRS\) có \(RS = 5\) cm; \(NR = 10\) cm. Độ dài cạnh \(MN\) là
\(5\) cm.
\(20\) cm.
\(10\) cm.
\(40\) cm.
Diện tích của hình bình hành \(ABCD\)trong hình dưới đây bằng bao nhiêu?
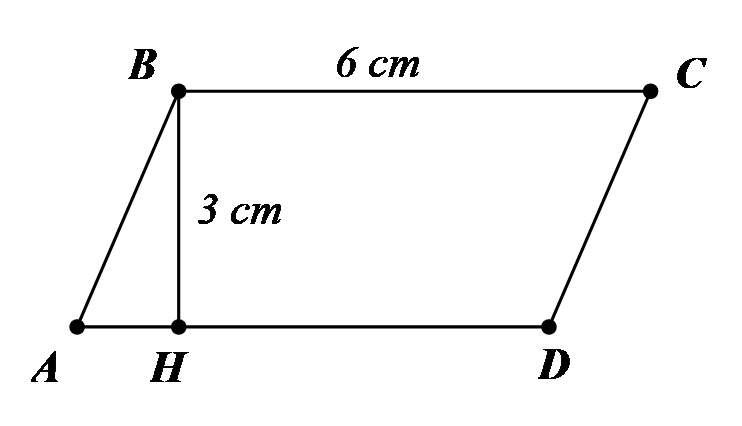
\(18\) cm.
\(18\) cm2.
\(9\) cm.
\(9\) cm2.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho số \(\overline {127x} .\)
a) Khi \(x \in \left\{ {0;\,\,2;\,\,4;\,6;\,\,8} \right\}\) thì số đã cho chia hết cho 2.
b) Khi \(x = 0\) thì số đã cho là bội của cả 2 và 5.
c) Khi \[x = 8\] thì số đã cho chỉ chia hết cho cả 3 và không chia hết cho 9.
d) Khi \[x = 8\] thì ta phân tích số này ra thừa số nguyên tố thì lũy thừa của số 2 có số mũ là 2.
Cho các hình sau: Hình tam giác đều, hình vuông, hình lục giác đều, hình chữ nhật, hình thoi, hình bình hành, hình thang cân.
a) Hình tam giác đều, hình vuông, hình lục giác đều có tất cả các cạnh bằng nhau.
b) Có 2 hình có hai đường chéo vuông góc với nhau.
c) Có 3 hình hai cạnh đối song song và các đường chéo bằng nhau.
d) Hình lục giác có độ dài đường chéo gấp đôi độ dài cạnh.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Cho tập hợp \(A = \left\{ {x \in \mathbb{N}*|50\,\, \vdots \,\,x,\,\,x < 30} \right\}.\) Tập hợp \(A\) có bao nhiêu phần tử?
Tìm số tự nhiên \(n\) thỏa mãn \(\left( {{2^3}:4} \right) \cdot {2^n} = 4.\)
Một trường Trung học cơ sở có 997 học sinh tham dự lễ tổng kết cuối năm. Ban tổ chức đã chuẩn bị những chiếc ghế băng 5 chỗ ngồi. Phải có ít nhất bao nhiêu ghế băng như vậy để tất cả học sinh đều có chỗ ngồi?
Nếu cạnh của một hình vuông tăng gấp 3 lần thì diện tích của nó tăng gấp bao nhiêu lần?
B. TỰ LUẬN (3,0 điểm)
(1,5 điểm)
1) Thực hiện phép tính (tính hợp lí nếu có thể):
a) \({6^2}:4 \cdot 6 + 2 \cdot {5^2} - {2^3}.\)b) \[26 \cdot 7 - 17 \cdot 9 + 13 \cdot 26 - 17 \cdot 11.\]
2) Tìm số tự nhiên \(x,\) biết: \({5^3} - 3\left( {x + 3} \right) = 65.\)
(1,0 điểm) Trên một mảnh đất hình chữ nhật có chiều dài \(40\) m, chiều rộng \(25\) m. Người ta làm một sân khấu hình thang cân có kích thước như hình bên dưới.
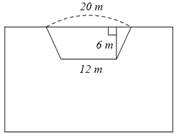
a) Tính diện tích mảnh đất và sân khấu.
b) Để trang trí sân khấu người ta phải trả cho mỗi mét vuông sân khấu là \(500 000\) đồng, còn khán đài phía dưới được trang trí bao quanh, mỗi mét bao quanh sân khấu chi phí là \(200 000\) đồng (phần trang trí khán đài sẽ không trang trí lên phần sân khấu). Tính tổng chi phí trang trí sân khấu và khán đài.
(0,5 điểm) Trên một bàn cờ vua, Minh muốn xếp gạo vào ô vuông theo quy luật sau: ô thứ nhất bỏ vào 1 hạt, ô thứ hai bỏ và 2 hạt, ô thứ ba bỏ vào 4 hạt, ô thứ tư bỏ vào 8 hạt và cứ như vậy, ở ô tiếp theo xếp số hạt gạo gấp đôi ô trước đó cho đến khi hết 64 ô trong bàn cờ. Hãy tính tổng số hạt gạo được Minh xếp lên bàn cờ vua và chứng minh rằng tổng số hạt gạo đó là một số chia hết cho 15.








