Bộ 10 đề thi giữa kì 1 Toán 6 Chân trời sáng tạo có đáp án - Đề 7
13 câu hỏi
Trong các tập hợp sau đây, tập hợp có một phần tử là
\(\left\{ {x;\,\,y} \right\}\)
\(\left\{ x \right\}\)
\(\left\{ {x;\,\,1} \right\}\)
\(\left\{ {1;\,\,y} \right\}\).
Trong các đồng hồ sau, đồng hồ chỉ \(8\) giờ đúng là đồng hồ nào trong hình?
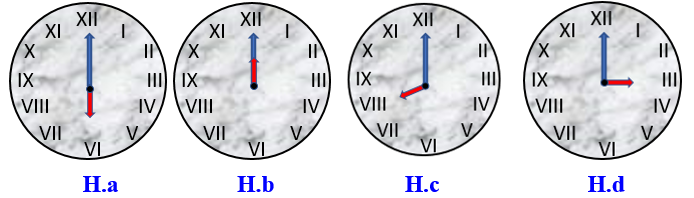
a
b
c
d.
Giá trị của \[x\] trong phép tính \[{2^{x + 1}}\,\,.\,\,{2^2} = 16\] là
4
3
1
4.
Nếu \[a\,\, \vdots \,\,5;\;\,\,b\,\, \vdots \,\,5;\;\,\,c\,\, \vdots \,{\rm{ }}5\] thì kết luận nào sau đây là đúng?
\[\left( {a + b + c} \right)\,\, \vdots \,\,2\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,5\]
\[\left( {a + b + c} \right)\,\,\cancel{ \vdots }\,\,5\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,25\].
Trong các khẳng định sau, khẳng định nào là đúng nhất?
Số nguyên tố là số chỉ có hai ước
Hợp số là số có hai ước
Hợp số là số tự nhiên lớn hơn \(1\) có ba ước
Hợp số là số tự nhiên lớn hơn \(1\), có nhiều hơn \(2\) ước.
Biển báo nào sau đây là hình vuông?

Hình 3
Hình 1
Hình 2
Hình 4.
Trong các khẳng định dưới đây, khẳng định nào là sai?
Cho hình thoi \[ABCD\]có
\[AB\] song song với \[CD\] và \[BC\] song song với \[AD\]
\[AB = BC = CD = AD\]
\[AC\] và \[BD\] vuông góc với nhau
Bốn góc đỉnh \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\] bằng nhau.
Một miếng gỗ hình thoi có kích thước hai đường chéo là \[5\,\,{\rm{cm}};\,\,8\,\,{\rm{cm}}\]. Diện tích của miếng gỗ là
\[20\,\,{\rm{c}}{{\rm{m}}^2}\]
\[12\,\,{\rm{c}}{{\rm{m}}^2}\]
\[24\,\,{\rm{c}}{{\rm{m}}^2}\]
\[10\,\,{\rm{c}}{{\rm{m}}^2}\].
(a) Viết tập hợp \(M\) các số tự nhiên lớn hơn \(12\) và không lớn hơn \(21\) bằng cách liệt kê phần tử.
(b) Vào đầu năm học mới, cô giáo chia tổ \(1\) gồm các thành viên trong tập hợp ID 10 NHOM PBT TRUNG BINH YEU TOAN 6 STT 60
\(T\) ={Lan; Minh; Hải; Tú; Kha; Vy; Châu} (lớp không có trường hợp nào trùng tên). Trong các thành viên Như, Tú, Kha; Hoàng, An, thành viên nào không thuộc tập hợp \(T\)?
Một trường THCS tổ chức cho học sinh đi trải nghiệm thực tế ở nhà máy thủy điện Hoà Bình. Sau khi học sinh đăng kí, ban tổ chức tính toán và thấy rằng nếu xếp mỗi xe 36 học sinh, 40 học sinh hay 45 học sinh đều vừa đủ. Tính số học sinh đi trải nghiệm biết rằng số học sinh tham gia trong khoảng 1 000 đến 1 100 học sinh.
Thực hiện phép tính (tính nhanh nếu có thể):
(a) \[237 + 86 + 63 + 214\]
(b) \[38\,\,.\,\,37 + 37\,\,.\,\,62\]
(c) \[{5^{12}}:{5^{10}} + 360:10 - {2024^0}\]
(d) \(321 - 21.\left[ {\left( {{{2.3}^3} + {4^4}:32} \right) - 52} \right]\).
Tìm \[x\], biết:
(a) \(5\left( {x + 1} \right) = 35\)
(b) \[2x - 138{\rm{ }} = {2^3}\,\,.\,\,{3^2}.\]
Chứng tỏ rằng: \(A = 1 + 4 + {4^2} + {4^3} + ... + {4^{2021}}\) chia hết cho 21.








