12 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như hình vẽ bên dưới.
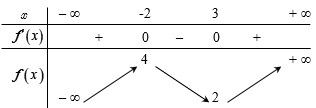
Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng nào dưới đây?
\[\left( {2;4} \right)\].
\[\left( { - \infty ;4} \right)\].
\[\left( {3; + \infty } \right)\].
\[\left( {2; + \infty } \right)\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên dưới.
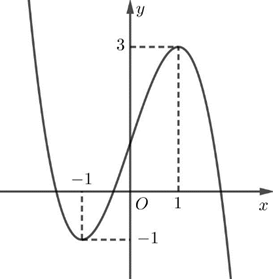
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
\(\left( {3;1} \right)\).
\(\left( { - 1; - 1} \right)\).
\(\left( {1;3} \right)\).
\(\left( {1;\, - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là sai?
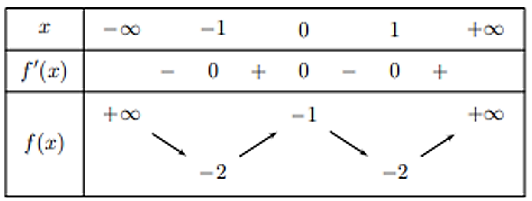
Hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng \( - 2\).
Hàm số \(y = f\left( x \right)\) không có giá trị lớn nhất.
Hàm số \(y = f\left( x \right)\) có giá trị lớn nhất bằng \[ - 1\].
Hàm số \(y = f\left( x \right)\) đạt giá trị nhỏ nhất tại \( \pm 1\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) là đường thẳng có phương trình
\(x = - 1.\)
\(y = - 1.\)
\(x = 2.\)
\(y = 2.\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên được cho dưới đây.
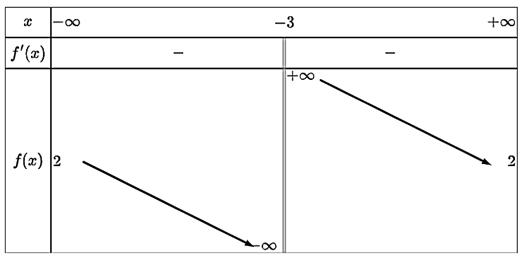
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) là
2
3.
0.
1.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình sau:
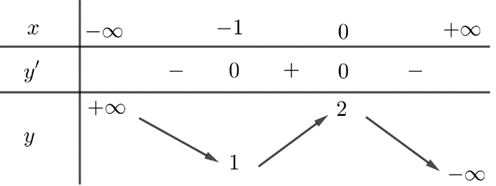
Số giao điểm của đồ thị hàm số đã cho với trục hoành là
0.
2
3
1.
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
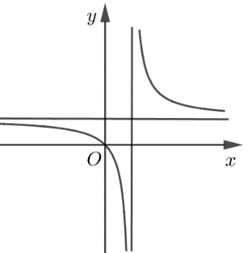
\(y = \frac{{x - 2}}{{x + 1}}\).
\(y = \frac{x}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = \frac{x}{{x + 1}}\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Chọn khẳng định đúng.
\[\overrightarrow {SB} = \overrightarrow {DA} + \overrightarrow {DC} - \overrightarrow {DS} \].
\[\overrightarrow {SB} = \overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DS} \].
\[\overrightarrow {SB} = \overrightarrow {DA} - \overrightarrow {DC} - \overrightarrow {DS} \].
\[\overrightarrow {SB} = \overrightarrow {DA} - \overrightarrow {DC} + \overrightarrow {DS} \].
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
\(\overrightarrow a \cdot \overrightarrow b = 0\).
\(\overrightarrow a \cdot \overrightarrow b = - 1\).
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
Cho hàm số \[y = f\left( x \right) = {x^3} + 3{x^2} - 1\]. Giá trị cực đại của hàm số đã cho là
-1.
0.
-2.
3.
Hàm số nào có bảng biến thiên như hình dưới đây?
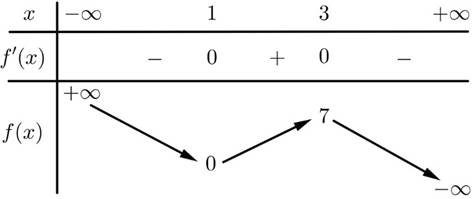
\[y = - \frac{7}{4}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x + 7\].
\[y = \frac{7}{4}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x + 7\].
\[y = - \frac{5}{3}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x\].
\[y = \frac{5}{3}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x\].
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(O,O'\) lần lượt là tâm của hình vuông \(ABCD\) và \(A'B'C'D'\). Độ dài vec tơ \(\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \) bằng
\(4a\).
\(6a\).
\(2a\).
\(a\).
