12 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\)có đồ thị như hình vẽ dưới đây.
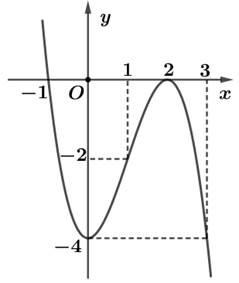
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào?
\(\left( {2; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\)
Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau:
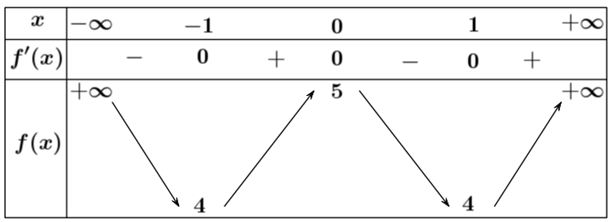
Giá trị cực đại của hàm số đã cho bằng
0.
5.
4.
-1.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình dưới đây.
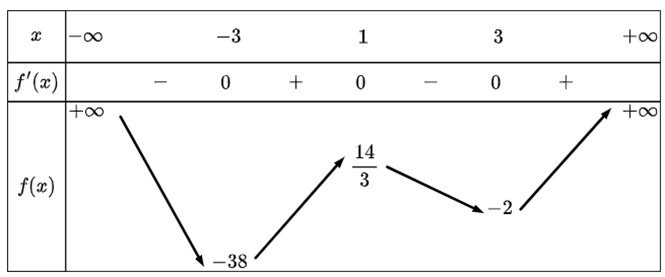
Khi đó giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 10;10} \right]\) bằng bao nhiêu?
\(\frac{{14}}{3}\).
\( - 38\).
\(\frac{{11}}{2}\).
\( - 2\).
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}(a,b,c,d \in \mathbb{R}\) có đồ thị là đường cong như hình dưới đây.

Đồ thị hàm số đã cho có đường tiệm cận đứng là
\(y = - 1\).
\(x = \frac{1}{3}\).
\(y = - \frac{1}{3}\).
\(x = - \frac{1}{3}\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2 - x}}{{2x + 1}}\) có phương trình là:
\(x = - \frac{1}{2}\).
\(y = 1\).
\(y = - \frac{1}{2}\).
\(x = 2\)
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình vẽ.
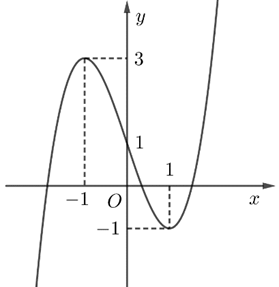
Đồ thị hàm số đã cho cắt trục tung tại điểm có tọa độ
\(\left( { - 1;\;3} \right)\).
\(\left( {1;\;0} \right)\).
\(\left( {1;\; - 1} \right)\).
\(\left( {0;\;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có bảng biến thiên như sau
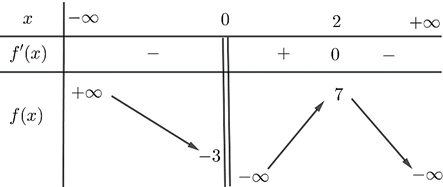
Số nghiệm của phương trình \(\frac{1}{3}f\left( x \right) + 1 = 0\) là
\(1.\)
\(3.\)
\(0.\)
\(2.\)
Cho tứ diện ABCD, gọi I là trung điểm của đoạn thẳng AB.
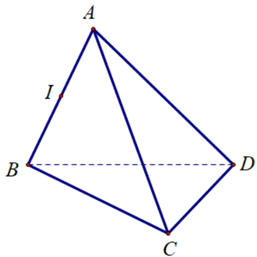
Vectơ \(\overrightarrow {AI} \) cùng hướng với vectơ nào sau đây?
\(\overrightarrow {CD} \).
\(\overrightarrow {AB} \).
\(\overrightarrow {CI} \).
\(\overrightarrow {BI} \).
Chohình lập phương\[ABCD.A'B'C'D'\].
![Title: 20241022132335314 - Description: \begin{tikzpicture}[scale=.7, font=\footnotesize, line join=round, line cap=round, >=stealth] \def\bc{4} % cạnh BC \def\ba{2} % cạnh BA \def\gocB{35} % góc B của đáy \coordinate[label=below left:$B$] (B) at (0,0); \coordinate[label=above left:$A$] (A) at (\gocB:\ba); \coordinate[label=below:$C$] (C) at (\bc,0); \coordinate[label=right:$D$] (D) at ($(C)-(B)+(A)$); \coordinate[label=above left:$A'$] (A') at ($(A)+(90:\bc)$); \coordinate[label=left:$B'$] (B') at ($(B)-(A)+(A')$); \coordinate[label=below right:$C'$] (C') at ($(C)-(A)+(A')$); \coordinate[label=right:$D'$] (D') at ($(D)-(A)+(A')$); \draw (B')--(B)--(C)--(D)--(D')--(A')--(B')--(C')--(D') (C)--(C'); \draw[dashed] (A')--(A)--(D) (A)--(B); \foreach \diem in {A,B,C,D,A',B',C',D'} \fill (\diem)circle(1.5pt); \end{tikzpicture}](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid58-1756388228.png)
Số đo góc \[\left( {\overrightarrow {BC} ,\overrightarrow {B'D'} } \right)\] bằng
\[45^\circ \].
\[90^\circ \].
\[60^\circ \].
\[135^\circ \]
Hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\)và có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right)\left( {{x^2} - 1} \right)\). Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng
\(\left( {1;2} \right)\).
\(\left( { - 2; - 1} \right)\).
\(\left( { - 1;0} \right)\).
\(\left( {0;1} \right)\).
Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\backslash \left\{ 1 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
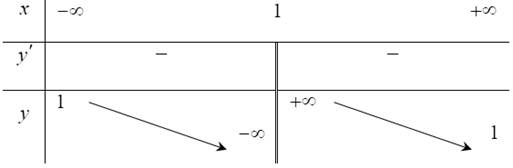
Bảng biến thiên trên của hàm số nào trong các hàm số sau?
\(y = \frac{{ - x + 2}}{{x - 1}}\).
\(y = \frac{{x + 2}}{{x - 1}}\).
\(y = \frac{{x + 2}}{{x + 1}}\).
\(y = \frac{{x - 3}}{{x - 1}}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh 2 (tham khảo hình vẽ dưới).
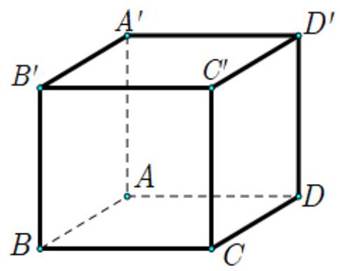
Độ dài vectơ \(\vec u = \overrightarrow {A'C'} - \overrightarrow {A'A} \) bằng
\(2\sqrt 2 \).
\(\sqrt 3 \).
\(2\sqrt 6 \).
\(2\sqrt 3 \).
