Bộ 3 đề KSCL đầu năm Toán 8 có đáp án - Đề 2
16 câu hỏi
Biểu thức nào sau đây không phải là biểu thức đại số?
\(5xy.\)
\[4x-2{y^3}.\]
\(\frac{{3x}}{0}.\)
\(5 \cdot \frac{1}{2} - 7.\)
Biểu thức nào sau đây là đa thức một biến?
\[x + 7xy.\]
\({x^5}-5y.\)
\[{x^2} + 9.\]
\(\frac{1}{x} + 13x - 5.\)
Tổng của hai đa thức \({y^2} + 2y\) và \(4y - {y^2}\) là
\(2{y^2} - 6y.\)
\(6y{\rm{.}}\)
\( - 2y{\rm{.}}\)
\(2y{\rm{.}}\)
Kết quả của phép tính \[3{x^2}:\;x\] là
\(3x.\)B. \(3{x^3}.\)C. \(x.\)D. \[3.\]
Cho tam giác \[ABC\] có số đo \(\widehat A,\,\,\widehat B,\,\,\widehat C\) theo thứ tự là \[80^\circ ;{\rm{ }}60^\circ ;{\rm{ }}40^\circ .\] Khẳng định nào sau đây là đúng?
\(BC > AC > AB.\)
\(BC < AC < AB.\)
</>
\[BC > AB > AC.\]
\(AB < BC < AC.\)
</>
Cho ba điểm \[A,{\rm{ }}B,{\rm{ }}C\] thẳng hàng và \[B\] nằm giữa \[A\] và \[C.\] Trên đường thẳng vuông góc với \[AC\] tại \[B\] ta lấy điểm \[H.\] Khi đó
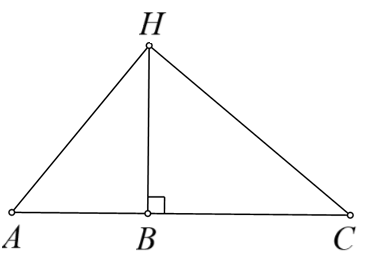
\(AH < BH.\)
</>
\(AH < AB.\)
</>
\[AH > BH.\]
\(AH = BH.\)
Gieo ngẫu nhiên xúc xắc một lần, kết quả có thể xảy ra đối với mặt xuất hiện là mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 4 chấm, mặt 5 chấm, mặt 6 chấm. Xét biến cố A: “Mặt xuất hiện của xúc xắc có số chấm là số lẻ” thì xác suất của biến cố này là
\(\frac{1}{3}\).
\(\frac{1}{6}\).
\(\frac{2}{3}\).
\(\frac{1}{2}\).
Tam giác \[ABC\] có độ dài cạnh đáy là \[a\,\,({\rm{cm}})\] và chiều cao tương ứng là \[h\,\,({\rm{cm}}).\] Biểu thức đại số tính diện tích tam giác \[ABC\] là
\[\frac{{a + h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
\[\frac{{a \cdot h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
\[a + h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
\[a \cdot h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Kết quả của phép tính \(2{x^2} \cdot \left( {3x + {x^2} - 5{x^3}} \right)\,\) là
\(6{x^3}\, + 2{x^4}\, - 10{x^5}.\)
\(5{x^3}\, + 2{x^4}\, - 10{x^5}.\)
\(6{x^3}\, + 2{x^4}\, - 10{x^6}.\)
\(6{x^3}\, - 2{x^4}\, - 10{x^5}.\)
Cho \(\Delta ABC\) có các đường trung tuyến \(AN\) và \(BM\) cắt nhau tại \(G\). Phát biểu nào sau là sai?
\(G\) là trọng tâm của \(\Delta ABC\).
\(CG\) đi qua trung điểm của \(AB\).
\(\frac{{GM}}{{AM}} = \frac{2}{3}\).
\[BG = 2GN\].
Hiệu của hai đa thức \[{x^2}--2x + 1\] và \[ - 2{x^2}--2x - 1\] là
\[3{x^2} + 2.\]
\[{x^2}.\]
\[3{x^2} - 2.\]
\[{x^2} - 2.\]
Bạn Nam xuất phát từ điểm \[M\] bên hồ bơi. Bạn ấy muốn bơi theo đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Nam phải bơi theo đường nào?
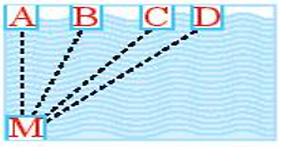
\[MA.\]
\[MB.\]
\[MC.\]
\[MD.\]
Phần II. Tự luận (7,0 điểm)
(1,5 điểm) Ngày 10 tháng 9 năm 2024 Liên đội trường THCS A phát động quyên góp sách vở đồ dùng học tập để ủng hộ học sinh vùng lũ. Lớp 8A có 41 học sinh mỗi học sinh ủng hộ \[x\] quyển vở, lớp 8B có 44 học sinh mỗi học sinh ủng hộ \[y\] quyển vở.
a) Nếu lớp 8A mỗi bạn ủng hộ 5 quyển vở thì tổng số vở lớp 8A quyên góp là bao nhiêu?
b) Viết biểu thức đại số biểu thị tổng số vở quyên góp của hai lớp 8A và 8B.
c) Tính tổng số vở quyên góp được của cả hai lớp nếu lớp 8A mỗi bạn ủng hộ 5 quyển và lớp 8B mỗi bạn ủng hộ được 4 quyển.
(2,5 điểm)
a) Tính giá trị của biểu thức \(3{x^2}y - 4xy + 1\) tại\(x = 1;\,\,y = - 2\).
b) Cho haiđa thức \[A(x) = 5{x^3} + 2{x^2} - 2x + 1\] và \(B(x) = - 5{x^3} - 2{x^2} - 3\).
Tính đa thức \(M(x) = A(x) + B(x)\)
c) Chứng tỏ rằng \[x = - 1\] nghiệm của đa thức \(M(x)\).
(2,5 điểm)Cho \(\Delta ABC\) vuông tại \[B\] có \[AD\] là tia phân giác của \[\widehat {BAC}\]\(\left( {D \in BC} \right)\). Kẻ \[DI \bot AC\,\,\left( {I \in AC} \right).\]
a) Chứng minh \(AB = AI\).
b) Từ \[C\] kẻ đường thẳng vuông góc với \[AD,\] cắt \[AD\] tại \[K.\] Hai đường thẳng \[CK\] và\[AB\] cắt nhau tại \[E.\] Chứng minh \[K\] là trung điểm của \[CE\] và \(\Delta AEC\) cân.
c) Chứng minh ba điểm \[E,{\rm{ }}D,{\rm{ }}I\] thẳng hàng.
(0,5 điểm) Ba nhà quyết định đào chung một cái giếng. Hỏi phải chọn vị trí giếng ở đâu để khoảng cách từ giếng đến các nhà bằng nhau?