Bộ 3 đề KSCL đầu năm Toán 7 có đáp án - Đề 2
18 câu hỏi
I. Phần trắc nghiệm (3,0 điểm)
Trong các cách viết sau đây, cách viết nào cho ta phân số?
\(\frac{1}{{6,8}}.\)
\(\frac{{ - 1,8}}{{ - 2}}.\)
\(\frac{7}{0}.\)
\(\frac{{ - 2}}{{15}}.\)
Viết số thập phân \(0,25\) dưới dạng phân số ta được là
\(\frac{5}{2}.\)
\(\frac{1}{4}.\)
\(\frac{3}{4}.\)
\(\frac{2}{5}.\)
Góc \(ABC\) có số đo bằng \(180^\circ \) thì góc \(ABC\) là
góc nhọn.
góc vuông.
góc bẹt.
góc tù.
Cho hình vẽ sau:

Khẳng định nào sau đây là sai?
Hai tia \(EF\) và tia \(ED\) đối nhau.
Hai tia \(Ea\) và tia \(Eb\) đối nhau.
Hai tia \(DF\) và tia \(Da\) trùng nhau.
Điểm \(F\) nằm giữa hai điểm \(E\) và \(D.\)
\(\frac{7}{{12}}\) của 84 bằng
35.
49.
84.
144.
Biểu đồ tranh dưới đây cho biết số lượt ô tô gửi tại một bãi đỗ xe vào các ngày trong tuần.
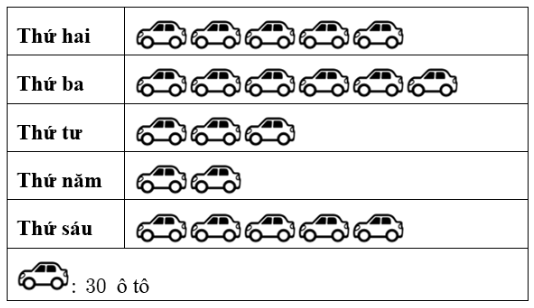
Số lượt ô tô đã gửi xe vào ngày thứ hai và thứ ba là
300.
630.
11.
330.
Làm tròn số \(56,087\) đến hàng phần trăm ta được
\(56,09.\)
\(56,08.\)
\(56.\)
\(56,1.\)
Tung đồ xu cân đối 50 lần, ta thu được kết quả như sau:
Sự kiện | Hai đồng sấp | Mật đồng sấp, một đồng ngửa | Hai đồng ngửa |
Số lần xuất hiện | 22 | 20 | 8 |
Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp” là
\(0,22.\)
\(0,4.\)
\(0,44.\)
\(0,16.\)
Cho điểm \(G\) nằm giữa hai điểm \(C\) và \(D\), biết \(CG = 3{\rm{ cm, }}CD = 8{\rm{ cm}}{\rm{.}}\) Khi đó, độ dài đoạn thẳng \(GD\) là
\(5{\rm{ cm}}{\rm{.}}\)
\(11{\rm{ cm}}{\rm{.}}\)
\(4{\rm{ cm}}{\rm{.}}\)
\(5{\rm{ dm}}{\rm{.}}\)
Cho phép thử gieo con xúc xắc 6 mặt. Sự kiện nào sau đây có thể xảy ra?
Số chấm lớn hơn 6.
Số chấm chia hết cho 7.
Số chấm lớn hơn 5.
Số chấm bằng 0.
Trong ngàu khai trương, cửa hàng đồ uống tại thị trấn Sơn Tây đã thống kê số cốc bán được của bốn loại nước như sau:
Tên đồ uống | Coco matcha | Matcha đá xay | Trà kombucha | Soda việt quất |
Số cốc bán được | 60 | 140 | 104 | 69 |
Số loại đồ uống cửa hàng bán được nhiều nhất trong ngày khai trương là
Coco matcha.
Matcha đá xay.
Trà kombucha.
Soda việt quất.
Quan sát hình vẽ bên và cho biết số đo \[\widehat {xOz}\] là
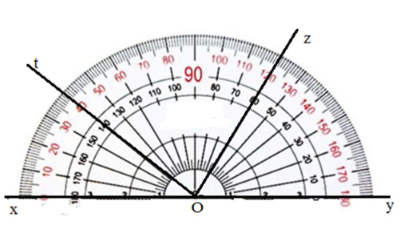
\(120^\circ .\)
\(60^\circ .\)
\(40^\circ .\)
\(140^\circ .\)
II. Phần tự luận (7,0 điểm)
(2,0 điểm)
1.1. Thực hiện phép tính (hợp lí nếu có thể):
a) \(\frac{{14}}{{23}} \cdot \left( { - \frac{8}{{11}}} \right) + \frac{{14}}{{23}} \cdot \left( { - \frac{3}{{11}}} \right)\).
b) \(9,51 \cdot \left( { - 14,75} \right) + 9,51 \cdot \left( { - 85,25} \right)\).
1.2. Tìm \(x,\) biết:
a) \(x - \frac{7}{4} = \frac{3}{{16}}.\)
b) \(\left( {5x - \frac{4}{9}} \right) \cdot \frac{8}{{27}} = \frac{8}{3}.\)
(1,5 điểm) Bạn An đọc một cuốn sách dày 360 trang trong ba ngày. Ngày thứ nhất, An đọc
được \(\frac{1}{4}\) tổng số trang sách. Ngày thứ hai An đọc được \(\frac{4}{9}\) số trang sách còn lại sau ngày thứ nhất.
a) Tính số trang sách bạn An đọc được trong ngày thứ nhất, ngày thứ hai và ngày thứ ba.
b) Số trang sách An đọc ngày thứ nhất chiếm bao nhiêu phần trăm tổng số trang sách của cuốn sách?
(1,0 điểm) Bạn Trang gieo 20 lần một con xúc xắc 6 mặt và ghi lại số chấm xuất hiện của mỗi lần gieo như nhau:
2 | 5 | 1 | 6 | 3 | 3 | 4 | 4 | 6 | 2 |
3 | 4 | 6 | 5 | 1 | 5 | 2 | 6 | 6 | 3 |
a) Hãy lập bảng thống kê theo mẫu sau:
Mặt ghi số chấm | 1 | 2 | 3 | 4 | 5 | 6 |
Số lần xuất hiện |
|
|
|
|
|
|
b) Tính xác suất thực nghiệm xuất hiện mặt có số chấm là số chẵn.
(1,5 điểm)Trên tia \(Bx\) lấy hai điểm \(E\) và \(F\) sao cho \(BE = 6{\rm{ cm, }}BF = 12{\rm{ cm}}{\rm{.}}\)
a) Tính độ dài đoạn thẳng \(EF.\)
b) Điểm \(E\) có là trung điểm của đoạn thẳng \(BF\) không? Vì sao?
c) Gọi \(I\) là trung điểm của \(EF\). Tính độ dài của đoạn thẳng \(BI.\)
(0,5 điểm)Tìm số tự nhiên biết \(n,\) biết: \(\frac{1}{{3 \cdot 5}} + \frac{1}{{5 \cdot 7}} + .... + \frac{1}{{n \cdot \left( {n + 2} \right)}} = \frac{1}{8}.\)


