Bộ 3 đề KSCL đầu năm Toán 12 có đáp án - Đề 3
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Đường cong ở hình sau là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
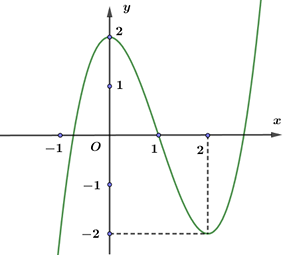
\(y = {x^3} - 3x + 2\).
\(y = {x^3} - 3{x^2} + 2\).
\(y = {x^3} - 6x + 2\).
\(y = - {x^3} + 3{x^2} + 2\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Đẳng thức nào sau đây là đẳng thức đúng?
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
\(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
\(\overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SA} + \overrightarrow {SD} \).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tích vô hướng của hai vec tơ \(\overrightarrow {BC'} \) và \(\overrightarrow {B'A} \) bằng
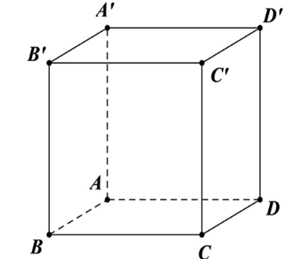
\({a^2}\).
\({a^2}\sqrt 2 \).
\( - {a^2}\).
\(\frac{{{a^2}\sqrt 2 }}{2}\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 2x + 4}}{{x - 3}}\) đi qua điểm nào sau đây?
\(M\left( {1;\,2} \right)\).
\(Q\left( {1;\, - 3} \right)\).
\(N\left( {3;\,1} \right)\).
\(P\left( {2;\,2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau:
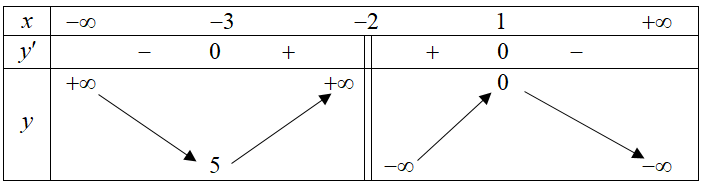
Giá trị cực đại của hàm số \(y = f\left( x \right)\) là:
\(0\).
\(1\).
\( - 3\).
\(5\).
Trong không gian \(Oxyz,\) cho \(\overrightarrow a = - 2\overrightarrow i + 4\overrightarrow j - 5\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là
\(\left( { - 2;4; - 5} \right)\).
\(\left( {2; - 4;5} \right)\).
\(\left( { - 5;4; - 2} \right)\).
\(\left( {5; - 4;2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến như sau:
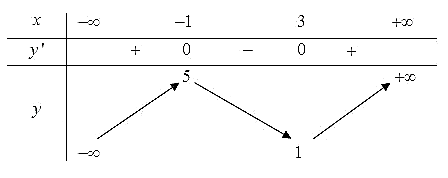
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( {1;5} \right)\).
\(\left( {3; + \infty } \right)\).
\(\left( { - 1;3} \right)\).
\(\left( {0;4} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;3} \right]\) như hình vẽ bên.
![Cho hàm số y = f( x ) liên tục và có bảng biến thiên trên đoạn [- 1;3] như hình vẽ bên.Khẳng định nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1754821452/1754821529-image5.png)
Khẳng định nào sau đây đúng?
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 0 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 3 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 2 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 1} \right)\) .
Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một nhóm học sinh thu được kết quả sau:
Thời gian (phút) | \(\left[ {0;4} \right)\) | \(\left[ {4;8} \right)\) | \(\left[ {8;12} \right)\) | \(\left[ {12;16} \right)\) | \(\left[ {16;20} \right)\) |
Số học sinh | 2 | 4 | 7 | 4 | 3 |
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
\(10,4\).
\(7\).
\(11,3\).
\(12,5\).
Cho mẫu số liệu với bộ ba tứ phân vị lần lượt là \({Q_1} = 11,5\); \({Q_2} = 14,5\); \({Q_3} = 21,3.\) Khi đó khoảng tứ phân vị của mẫu số liệu trên là
\(\Delta Q = 3,0\).
\(\Delta Q = 6,8\).
\(\Delta Q = 9,8\).
\(\Delta Q = 32,8\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(A\left( {1; - 2;3} \right);B\left( {2; - 3;4} \right)\).Tìm điểm \(M \in \left( {Oxy} \right)\) sao cho ba điểm \(A,B,M\) thẳng hàng.
\(M\left( {1;1;0} \right)\).
\(M\left( {3; - 4;5} \right)\).
\(M\left( { - 3;5;0} \right)\).
\(M\left( { - 2;1;0} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên dưới.
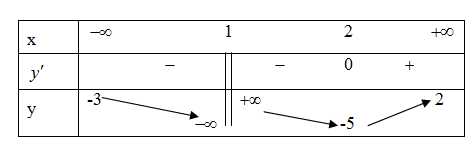
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và đường tiệm cận ngang?
\(1\).
\(2\).
\(3\).
\(4\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Cho hàm số \[y = f\left( x \right) = \frac{{a{x^2} + bx + 1}}{{cx + d}}\]đạt cực đại tại \[x = 0\]và có đồ thị như hình vẽ sau:
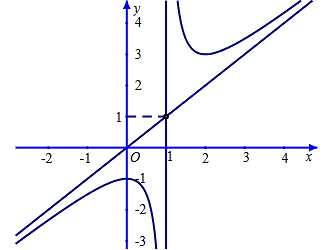
a) Giá trị của biểu thức \[a + b + c + d = 0.\]
b) Hàm số đồng biến trên \[\left( { - 1;0} \right).\]
c) Gọi \[A,B\]là các điểm cực trị của đồ thị hàm số; \[M\]là điểm di động trên trục \[Ox\] sao cho \[\widehat {AMB}\]không tù. Giá trị nhỏ nhất của hoành độ điểm \[M\]là 3.
d) Đường thẳng đi qua hai điểm cực trị của hàm số có phương trình: \[y = x - 1.\]
Cho hình chóp tứ giác đều \[S.ABCD\] có cạnh đáy bằng \[a\], \[O = AC \cap BD\] biết \[SO = \frac{{a\sqrt 3 }}{2}\]. Gọi \[M\]và \[N\] lần lượt là trung điểm của các cạnh \[AD\] và \[BC\].
a) \[\left( {SMN} \right) \bot \left( {ABCD} \right)\].
b) \[{V_{S.ABC}} = \frac{{\sqrt 3 {a^3}}}{{12}}\].
c) \[d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt 3 }}{3}\].
d) \[{\rm{cos}}\alpha = - \frac{1}{4}\] với \[\alpha \] là số đo góc nhị diện \[\left[ {B,SC,D} \right]\].
Có một chai, một vại to, một cốc, một chén và một vại nhỏ được xếp thành dãy theo thứ tự đó (tham khảo hình vẽ dưới đây), đựng các thứ nước khác nhau là: nước chè, cà phê, ca cao, sữa và bia. Nếu đem chiếc chén đặt vào giữa vật đựng chè và vật đựng sữa thì vật đựng chè và vật đựng ca cao sẽ cạnh nhau, vật đựng chè sẽ thay đổi thứ tự và vật đựng cà phê ở chính giữa.

a) Bia được đựng trong vại to.
b) Cà phê được đựng trong chén.
c) Chè được đựng trong vại nhỏ.
d) Sữa được đựng trong chai.
Phòng quản lí đào tạo trường Đại học Kinh tế quốc dân thống kê số giờ làm thêm của một nhóm sinh viên năm thứ tư của trường thu được kết quả như bảng sau:
Số giờ làm thêm (giờ/tuần) | \(\left[ {9;12} \right)\) | \(\left[ {12;15} \right)\) | \(\left[ {15;18} \right)\) | \(\left[ {18;21} \right)\) | \(\left[ {21;24} \right)\) |
Số sinh viên | \(6\) | \(12\) | \(4\) | \(2\) | \(1\) |
a) Giá trị đại diện của nhóm \(\left[ {9;12} \right)\) là \(10,5\).
b) Số giờ làm thêm trung bình của nhóm sinh viên trên trong một tuần là \(16,5\) giờ.
c) Nhóm chứa trung vị là \(\left[ {15;18} \right)\).
d) Tứ phân vị thứ ba là \(15,65\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc và có độ lớn lần lượt là \(25\)N và \(12\) N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(4\)N. Tính độ lớn của hợp lực của ba lực trên (làm tròn kết quả đến hàng phần chục theo đơn vị Newton).
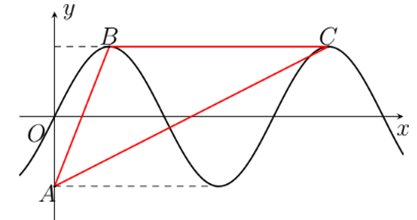
Cho đồ thị hàm số \(f\left( x \right) = 2\sin x\) như hình vẽ. Tính diện tích tam giác \(ABC\) (kết quả làm tròn đến hàng phần mười).
Một nhà xuất bản nhận in 4000 ấn phẩm. Nhà xuất bản có tất cả 14 máy in được cài đặt, hoạt động tự động và giám sát bởi 1 kĩ sư. Mỗi máy in có thể in được 30 ấn phẩm trong một giờ. Chi phí cài đặt máy in là 12 USD cho một máy, chi phí giám sát là 9 USD một giờ. Tính số máy in nhà xuất bản nên sử dụng để chi phí in là nhỏ nhất.
Năng lượng giải toả \(E\) của một trận động đất tại tâm chấn ở \(M\) độ Richter được xác định bởi công thức \(\log \left( E \right) = 11,4 + 1,5M\). Vào năm \(2024\), thành phố \(X\) xảy ra một trận động đất \(7,4\) độ Richter và năng lượng giải toả tại tâm chấn của động đất đó gấp \(11\) lần trận động đất xảy ra ở thành phố \(Y\) vào năm \(2023\). Hỏi khi đó, độ lớn của trận động đất tại thành phố \(Y\) là bao nhiêu độ Richter? (kết quả làm tròn đến hàng phần chục).
Phòng thí nghiệm \(B\) được giao làm hai thí nghiệm độc lập. Xác suất thành công trong từng thí nghiệm là 0,7. Phòng thành công ít nhất một thí nghiệm được coi là hoàn thành nhiệm vụ. Tính xác suất để phòng thí nghiệm \(B\) hoàn thành nhiệm vụ.


