Bộ 3 đề KSCL đầu năm Toán 12 có đáp án - Đề 1
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho cấp số cộng có số hạng đầu \[{u_1} = 2\], công sai \[d = - 4\]. Số hạng thứ năm của cấp số cộng là
\[512\].
\[ - 14\].
\[ - 512\].
\[ - 18\].
Thống kê số phút học bài ở nhà mỗi ngày của \[100\] học sinh ta có bảng phân bố tần số ghép nhóm như sau
Số phút | \[\left[ {30;60} \right)\] | \[\left[ {60;90} \right)\] | \[\left[ {90;120} \right)\] | \[\left[ {120;150} \right)\] |
Số học sinh | \[18\] | \[15\] | \[42\] | \[25\] |
Số học sinh có thời gian học ít hơn \[2\] tiếng trong số học sinh trên là
\[15\].
\[33\].
\[75\].
\[18\].
Trong không gian với hệ tọa độ \[Oxyz\], cho điểm \[A\left( {1;2; - 1} \right)\]. Tọa độ hình chiếu vuông góc của \[A\] trên mặt phẳng \[\left( {Oyz} \right)\] là
\[\left( {0;2; - 1} \right)\].
\[\left( {1;0;0} \right)\].
\[\left( {1;2;0} \right)\].
\[\left( {1;0; - 1} \right)\].
Gọi \[M,m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[f\left( x \right) = {x^4} - 2{x^2} - 1\] trên đoạn \[\left[ { - 1;2} \right]\]. Giá trị của biểu thức \[M + 2m\] bằng
\[3\].
\[5\].
\[6\].
\[4\].
Cho khối lăng trụ đều có diện tích đáy bằng \[2\,\,({{\rm{m}}^{\rm{2}}})\] và chiều cao bằng \[3\,\,{\rm{(m)}}\]. Thể tích khối lăng trụ đã cho bằng
\[\frac{{3\sqrt 3 }}{2}\,({{\rm{m}}^3})\].
\[2\,({{\rm{m}}^3})\].
\[\frac{{\sqrt 3 }}{2}({{\rm{m}}^3})\].
\[6\,({{\rm{m}}^3})\].
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau:
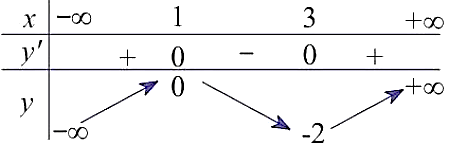
Hàm số đã cho nghịch biến trên khoảng
\[\left( { - 2;0} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( {3; + \infty } \right)\].
\[\left( {1;3} \right)\].
Đường tiệm cận xiên của đồ thị hàm số \[y = 2x - 1 + \frac{1}{x}\] có phương trình là:
\[y = 1 - 2x\].
\[y = 2x\].
\[y = 2x - 1\].
\[y = - 2x\].
Hàm số nào dưới đây có đồ thị như hình vẽ sau?
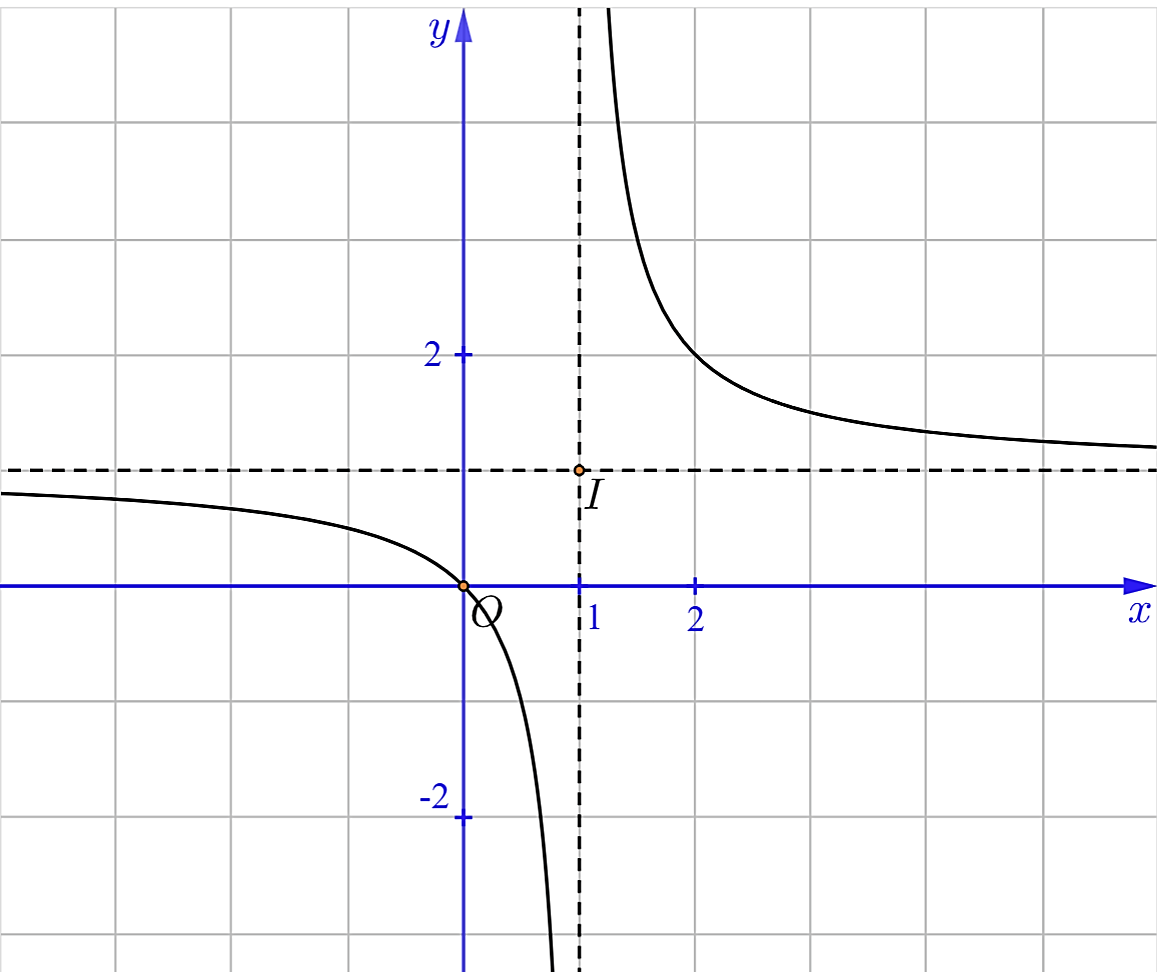
\[y = \frac{x}{{x + 1}}\].
\[y = - \frac{x}{{x - 1}}\].
\[y = - \frac{x}{{x + 1}}\].
\[y = \frac{x}{{x - 1}}\].
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây.
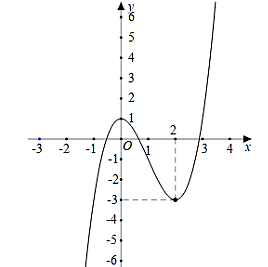
Giá trị cực tiểu của hàm số đã cho là
\( - 3\).
\(2\).
\(1\).
\(0\).
Tập nghiệm của bất phương trình \[{\log _{\frac{1}{3}}}\left( {x - 1} \right) > - 2\] là
\(\left( {10; + \infty } \right)\).
\(\left( {1;10} \right)\).
\(\left( {9; + \infty } \right)\).
\(\left( { - \infty ;10} \right)\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Đẳng thức nào sau đây là đẳng thức đúng?
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
\(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
\(\overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SA} + \overrightarrow {SD} \).
Cho \(A\) và \(B\) là hai biến cố độc lập. Biết xác suất của biến cố \(A\) là \(0,4\); xác suất của biến cố \(B\) là \(0,3\). Xác suất của biến cố \(A \cup B\) là
\(0,12\).
\(0,58\).
\(0,7\).
\(0,82\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Cho hàm số \(f\left( x \right) = 4\sin x + 2x\).
a) Đạo hàm của hàm số đã cho là \(f'\left( x \right) = - 4\cos x + 2\).
b) \(f\left( 0 \right) = 0\), \(f\left( \pi \right) = 2\pi \).
c) Nghiệm của phương trình \(f'\left( x \right) = 0\) trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{{2\pi }}{3}\).
d) Giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ {0;\pi } \right]\) là \(2\pi + 1\).
Hình minh họa sơ đồ một ngôi nhà trong hệ trục tọa độ\[Oxyz\], trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.
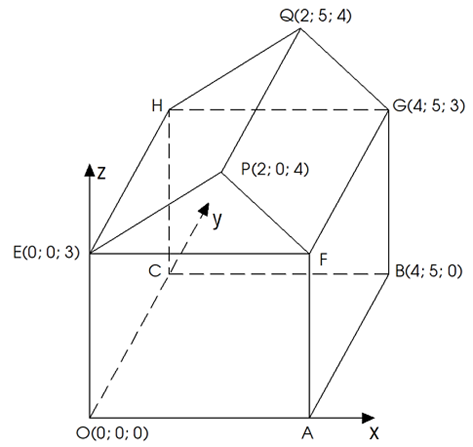
a) Tọa độ điểm \[A\] là \[\left( {4;0;0} \right).\]
b) \[\overrightarrow {OQ} = \left( {2;5;4} \right).\]
c) Tọa độ \[\overrightarrow {AH} = \left( {4;5;3} \right).\]
d) \[C\left( {0;5;0} \right).\]
Theo báo cáo của một cơ sở sản xuất nước tinh khiết, nếu mỗi ngày cơ sở này sản xuất \(x\,({{\rm{m}}^{\rm{3}}})\) nước tinh khiết thì phải trả chi phí các khoản sau: 3 triệu đồng chi phí cố định; \(0,15\) triệu đồng cho mỗi mét khối sản phẩm; \(0,0003{x^2}\) triệu đồng chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là \(200\,\,{{\rm{m}}^{\rm{3}}}\). Gọi \(C\left( x \right)\) là chi phí sản xuất \(x\,({{\rm{m}}^{\rm{3}}})\) sản phẩm mỗi ngày và \(\overline c \left( x \right)\) là chi phí trung bình mỗi mét khối sản phẩm.
a) \(\overline c \left( x \right) = 0,0003x + 0,15 + \frac{3}{x}\).
b) \(C\left( x \right) = 0,0003{x^2} + 0,15x + 5\).
c) Chi phí sản xuất \(100\,\,{{\rm{m}}^{\rm{3}}}\) nước tinh khiết là 20 triệu đồng.
d) Chi phí trung bình mỗi mét khối sản phẩm thấp nhất khi sản lượng nước tinh khiết trong ngày là \(100\,\,{{\rm{m}}^{\rm{3}}}\).
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình sau đây.
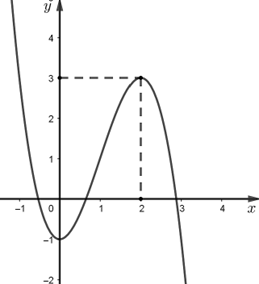
a) Giá trị cực tiểu của hàm số\(f\left( x \right)\)bằng \( - 1\).
b)Phương trình \({\log _3}\left( {f\left( x \right) + 6} \right) = 2\) có 2 nghiệm.
c)Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1;3} \right)\).
d) Tổng\(2025a + b + c + d = - 2023\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hàm số \(y = f\left( x \right) = \frac{{2{x^2} + 26x + 18}}{{x + 13}}\) có điểm cực tiểu \(x = {x_1}\) và điểm cực đại \(x = {x_2}\). Tính \(P = - 2{x_1} + {x_2}\).
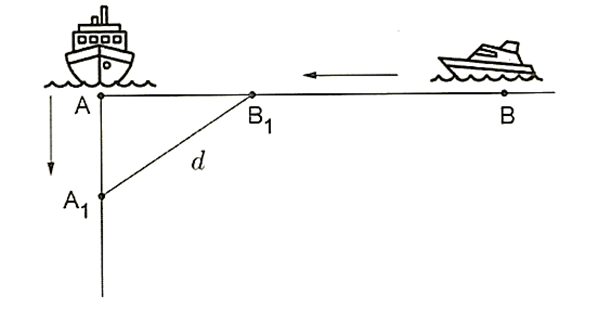
Hai con tàu \(A\) và \(B\) đang ở cùng một vĩ tuyến và cách nhau 6 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu \(A\) chạy về hướng Nam với vận tốc 5 hải lí/ giờ, còn tàu \(B\) chạy về vị trí hiện tại của tàu \(A\) với vận tốc 7 hải lí/ giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần trăm)?
Cho tứ diện \(SABC\) có \(G\) là trọng tâm tam giác \(ABC\) và \(I\) là trọng tâm tam giác \(GBC\). Biết \(\overrightarrow {SI} = x\overrightarrow {SA} + y\overrightarrow {SB} + z\overrightarrow {SC} \), tính giá trị biểu thức \(9\left( {x - y + z} \right)\).
Khảo sát thời gian tập thể dục của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau.
Thời gian (phút) | \(\left[ {0;20} \right)\) | \(\left[ {20;40} \right)\) | \(\left[ {40;60} \right)\) | \(\left[ {60;80} \right)\) | \(\left[ {80;100} \right)\) |
Số học sinh | \(5\) | \(9\) | \(12\) | \(10\) | \(6\) |
Trung bình mỗi học sinh tập bao nhiêu phút mỗi ngày? (kết quả làm tròn đến hàng phần mười).
Một nhóm gồm 3 học sinh lớp 10, 3 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngồi cùng vào một hàng có 9 ghế, mỗi học sinh ngồi 1 ghế. Tính xác suất để 3 học sinh lớp 10 không ngồi 3 ghế liền nhau (kết quả làm tròn đến hàng phần trăm).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng 2. Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Biết hai mặt phẳng \(\left( {SDM} \right)\) và \(\left( {SCN} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\), đồng thời khoảng cách giữa \(DM\) và \(SC\) bằng \(\frac{{12}}{7}\). Thể tích khối chóp \(S.ABCD\) bằng bao nhiêu?


