Bộ 3 đề KSCL đầu năm Toán 12 có đáp án - Đề 2
21 câu hỏi
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Nghiệm của phương trình \({\log _2}x = 3\) là
\(x = 3\).
\(x = 2\).
\(x = {3^2}\).
\(x = {2^3}\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 4} \right)\left( {x + 2} \right)\left( {x - 3} \right)\) và liên tục trên \(\mathbb{R}\). Số điểm cực trị của hàm số là
\(5\).
\(2\).
\(3\).
\(1\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới.
![Cho hàm số y = f( x ) có bảng biến thiên như hình dưới. Giá trị lớn nhất của hàm số đã cho trên đoạn [ - 2;4] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1754820316/1754820394-image1.png)
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 2;4} \right]\) bằng
\( - 1\).
\(10\).
\(1\).
\(8\).
Cho hàm số đa thức bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ.
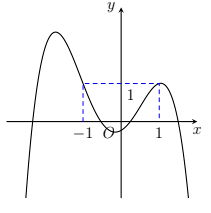
Phương trình \(f\left( x \right) - 1 = 0\) có bao nhiêu nghiệm thực phân biệt?
\(3\).
\(1\).
\(2\).
\(4\).
Đồ thị hàm số nào sau đây có hình dạng như hình vẽ?
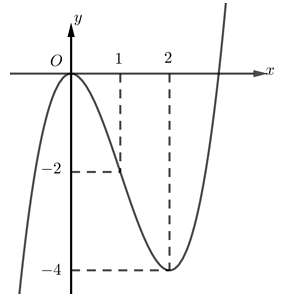
\(y = {x^3} + 3x\).
\(y = {x^3} - 3x\).
\(y = {x^3} - 3{x^2}\).
\(y = {x^3} + 3{x^2}\).
Tập nghiệm của bất phương trình \[{\left( {\frac{1}{2}} \right)^x} < \frac{1}{8}\] là
</>
\(\left( {3; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
\(\left[ {3; + \infty } \right)\).
\(\left( { - \infty ;3} \right]\).
Trong không gian \[Oxyz\], cho \[\overrightarrow a = 2\overrightarrow i - 3\overrightarrow j + \overrightarrow k \]. Toạ độ của \[\overrightarrow a \] là:
\[\left( { - 2;1;3} \right)\].
\[\left( {2; - 3;1} \right)\].
\[\left( {2;1;3} \right)\].
\[\left( {2;1; - 3} \right)\].
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội \(q = 5\). Số hạng \({u_3}\) của cấp số nhân đã cho là
\({u_3} = 50\).
\({u_3} = 12\).
\({u_3} = 10\).
\({u_3} = 7\).
Cho hình hộp \(ABCD.EFGH\).
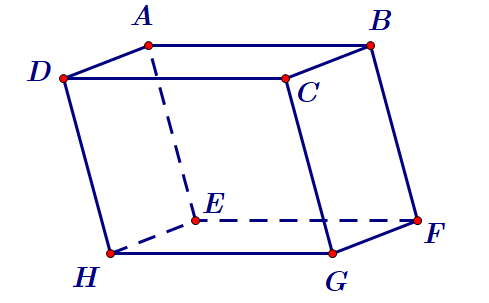
Vectơ nào sau đây bằng vectơ \(\overrightarrow {FH} \)?
\(\overrightarrow {BD} \).
\(\overrightarrow {DB} \).
\(\overrightarrow {BA} \).
\(\overrightarrow {AB} \).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, tam giác \[SAD\] đều. Góc giữa hai đường thẳng \[BC\] và \[SA\] bằng
\[60^\circ \].
\[30^\circ \].
\[90^\circ \].
\[45^\circ \].
Trong tuần lễ bảo vệ môi trường, các học sinh khối 12 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thông báo kết quả thu nhặt vỏ chai của học sinh khối 12 ở bảng sau:
Số vỏ chai nhựa | \[\left[ {10,5;15,5} \right)\] | \[\left[ {15,5;20,5} \right)\] | \[\left[ {20,5;25,5} \right)\] | \[\left[ {25,5;30,5} \right)\] | \[\left[ {30,5;35,5} \right)\] |
Số học sinh | \[53\] | \[82\] | \[48\] | \[39\] | \[18\] |
Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?
\[19,51\].
\[19,59\].
\[20,1\].
\[18,3\].
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x - 2}}{{x + 1}}\) là
\(y = - 2\).
\(y = 1\).
\(x = - 1\).
\(x = 2\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Quảng cáo là hình thức tuyên truyền được trả phí hoặc không để thực hiện việc giới thiệu thông tin về sản phẩm, dịch vụ, công ty hay ý tưởng, quảng cáo là hoạt động truyền thông phi trực tiếp giữa người với người mà trong đó người muốn truyền thông phải trả tiền cho các phương tiện truyền thông đại chúng để đưa thông tin đến thuyết phục hay tác động đến người nhận thông tin. Khảo sát tại một công ty A cho thấy nếu chi \(x\) triệu đồng để quảng cáo một loại sản phẩm thì số sản phẩm công ty A bán được là \(S\left( x \right) = - 2{x^3} + 27{x^2} + 216x + 150\) với \(x \in \left[ {0;15} \right].\)
a) \(S'\left( x \right) = - 6{x^2} + 54x + 216.\)
b) Nếu không chi cho quảng cáo thì số lượng sản phẩm công ty A bán được là 391 sản phẩm.
c) Nếu công ty A chi 11 triệu đồng đến 12 triệu đồng cho quảng cáo loại sản phẩm này thì số lượng sản phẩm công ty A bán được đạt tối đa bằng 3131 triệu đồng.
d) Nếu công ty A chi từ 11 triệu đồng đến 12 triệu đồng cho quảng cáo loại sản phẩm này thì số lượng sản phẩm bán được sẽ tăng.
Anh \(X\) nhận hợp đồng làm việc cho một công ty \(Y\) với lương tháng đầu là \(6\) triệu. Trong điều khoản về lương, nếu anh \(X\) hoàn thành nhiệm vụ thì cứ sau \(6\) tháng được tăng \(15\% \) so với mức lương trước đó. Trong suốt quá trình làm việc, anh \(X\) đều hoàn thành nhiệm vụ của mình và được tăng lương đúng kỳ hạn.
a) Mức lương của anh \(X\) ở tháng thứ \(11\) kể từ khi ký hợp đồng lao động là \(6,9\) triệu đồng.
b) Coi mỗi \(6\) tháng anh \(X\) nhận lương như nhau là một kỳ và \({u_n}\) là lương mỗi tháng của kỳ thứ \(n\), khi đó \(\left( {{u_n}} \right)\) là một cấp số cộng với công sai \(d = 1,15\).
c) Tổng số tiền anh \(X\) nhận được từ tiền lương của công ty \(Y\) sau \(4\) năm kể từ ngày ký hợp đồng (làm tròn đến hàng phần trăm) là \(494,17\) triệu đồng.
d) Khi nhận lương hàng tháng, nếu anh \(X\) phải đóng bảo hiểm thất nghiệp \(1,5\% \) số tiền lương được nhận thì sau \(10\) năm kể từ ngày ký hợp đồng anh \(X\) đã đóng số tiền bảo hiểm thất nghiệp (làm tròn đến hàng phần trăm) là \(55,32\) triệu đồng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một vật chuyển động. Quãng đường \(s\left( t \right)\) (tính theo mét) vật đi được sau khoảng thời gian \(t\) (tính theo giây), \(t \ge 0\), được mô tả là một hàm số bậc ba có đồ thị như hình vẽ dưới đây.
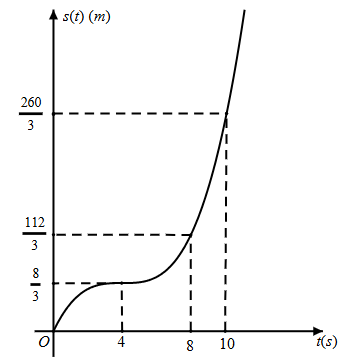
Hỏi trong \(10\) giây đầu tiên, khoảng thời gian vật chuyển động nhanh dần kéo dài bao nhiêu giây?
Cho hình chóp đều \(S.ABC\) có cạnh đáy bằng \(1\). Góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) (kết quả viết dưới dạng số thập phân).
Bạn Tiến làm một bài kiểm tra gồm \[20\]câu hỏi trắc nghiệm nhiều lựa chọn. Mỗi câu hỏi có \[4\]phương án trả lời và chỉ có một phương án đúng, trả lời đúng mỗi câu được \[0,5\]điểm. Bạn ấy đã làm đúng \[12\]câu, trong những câu còn lại có \[2\]câu bạn ấy đã loại được một phương án sai. Do quá sát giờ nộp bài nên bạn ấy đã trả lời bằng cách chọn ngẫu nhiên. Gọi \[P\]là xác suất để bạn Tiến được \[9\]điểm. Tính \[1000P\](làm tròn kết quả đến hàng phần trăm).
Lúc \(12\) giờ, kim giờ và kim phút của một chiếc đồng hồ trùng nhau. Hỏi từ lúc đó đến khi hai kim trùng nhau lần đầu tiên, kim phút quay được một góc lượng giác bao nhiêu radian (làm tròn đến kết quả đến hàng phần chục)?
B. TỰ LUẬN
Cho khối lăng trụ \[ABC.A'B'C'\]có đáy là tam giác đều cạnh bằng 5. Hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \[\left( {ABC} \right)\] trùng với trọng tâm \[G\] của tam giác \[ABC\]. Biết khoảng cách giữa hai đường thẳng \[AA'\] và \[BC\]bằng \(\frac{{5\sqrt 3 }}{4}\). Tính thể tích của khối lăng trụ đã cho.
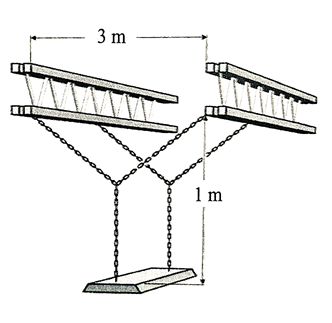
Trong một cửa hàng, nhà quản lý dự định treo một đồ trang trí trên cao. Vật trang trí được đặt trên giá đỡ nằm dưới thanh treo 1 m. Biết khoảng cách giữa hai thanh treo là 3 m. Xác định tổng độ dài nhỏ nhất của các đoạn dây xích.
Trong không gian \(Oxyz\), một chiếc máy quay phim được đặt trên một giá đỡ ba chân với điểm đặt \(S\left( {0;0;5} \right)\) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \(A\left( {0;1;0} \right),\,\,B\left( { - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0} \right),\)\(C\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0} \right)\) (hình vẽ). Biết lực tác dụng của máy quay phim lên các giá đỡ \(SA,\,\,SB,\,\,SC\) lần lượt là \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) và trọng lượng của chiếc máy là \(60\,{\rm{N}}\), giá trị của \(\left| {\overrightarrow {{F_1}} } \right| + \left| {\overrightarrow {{F_2}} } \right| + \left| {\overrightarrow {{F_3}} } \right|\) bằng bao nhiêu Newton?