12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Đường cong ở hình sau là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
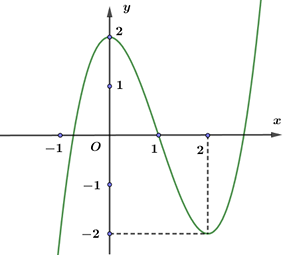
\(y = {x^3} - 3x + 2\).
\(y = {x^3} - 3{x^2} + 2\).
\(y = {x^3} - 6x + 2\).
\(y = - {x^3} + 3{x^2} + 2\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Đẳng thức nào sau đây là đẳng thức đúng?
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
\(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
\(\overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SA} + \overrightarrow {SD} \).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tích vô hướng của hai vec tơ \(\overrightarrow {BC'} \) và \(\overrightarrow {B'A} \) bằng
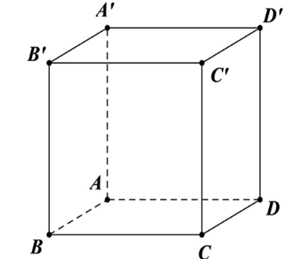
\({a^2}\).
\({a^2}\sqrt 2 \).
\( - {a^2}\).
\(\frac{{{a^2}\sqrt 2 }}{2}\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 2x + 4}}{{x - 3}}\) đi qua điểm nào sau đây?
\(M\left( {1;\,2} \right)\).
\(Q\left( {1;\, - 3} \right)\).
\(N\left( {3;\,1} \right)\).
\(P\left( {2;\,2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau:
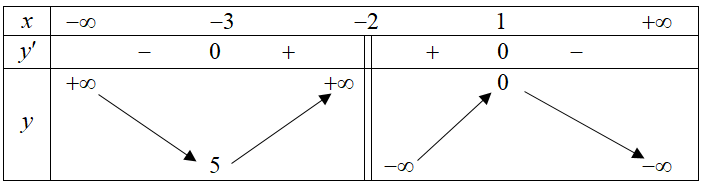
Giá trị cực đại của hàm số \(y = f\left( x \right)\) là:
\(0\).
\(1\).
\( - 3\).
\(5\).
Trong không gian \(Oxyz,\) cho \(\overrightarrow a = - 2\overrightarrow i + 4\overrightarrow j - 5\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là
\(\left( { - 2;4; - 5} \right)\).
\(\left( {2; - 4;5} \right)\).
\(\left( { - 5;4; - 2} \right)\).
\(\left( {5; - 4;2} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến như sau:
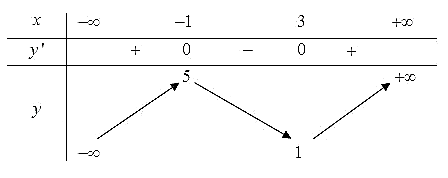
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( {1;5} \right)\).
\(\left( {3; + \infty } \right)\).
\(\left( { - 1;3} \right)\).
\(\left( {0;4} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;3} \right]\) như hình vẽ bên.
![Cho hàm số y = f( x ) liên tục và có bảng biến thiên trên đoạn [- 1;3] như hình vẽ bên.Khẳng định nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1754821452/1754821529-image5.png)
Khẳng định nào sau đây đúng?
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 0 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 3 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 2 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 1} \right)\) .
Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một nhóm học sinh thu được kết quả sau:
|
Thời gian (phút) |
\(\left[ {0;4} \right)\) |
\(\left[ {4;8} \right)\) |
\(\left[ {8;12} \right)\) |
\(\left[ {12;16} \right)\) |
\(\left[ {16;20} \right)\) |
|
Số học sinh |
2 |
4 |
7 |
4 |
3 |
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
\(10,4\).
\(7\).
\(11,3\).
\(12,5\).
Cho mẫu số liệu với bộ ba tứ phân vị lần lượt là \({Q_1} = 11,5\); \({Q_2} = 14,5\); \({Q_3} = 21,3.\) Khi đó khoảng tứ phân vị của mẫu số liệu trên là
\(\Delta Q = 3,0\).
\(\Delta Q = 6,8\).
\(\Delta Q = 9,8\).
\(\Delta Q = 32,8\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(A\left( {1; - 2;3} \right);B\left( {2; - 3;4} \right)\).Tìm điểm \(M \in \left( {Oxy} \right)\) sao cho ba điểm \(A,B,M\) thẳng hàng.
\(M\left( {1;1;0} \right)\).
\(M\left( {3; - 4;5} \right)\).
\(M\left( { - 3;5;0} \right)\).
\(M\left( { - 2;1;0} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên dưới.
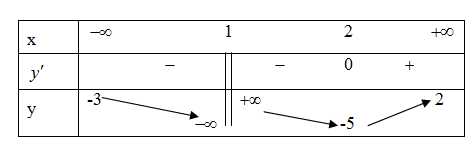
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và đường tiệm cận ngang?
\(1\).
\(2\).
\(3\).
\(4\).
