12 câu hỏi
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Nghiệm của phương trình \({\log _2}x = 3\) là
\(x = 3\).
\(x = 2\).
\(x = {3^2}\).
\(x = {2^3}\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 4} \right)\left( {x + 2} \right)\left( {x - 3} \right)\) và liên tục trên \(\mathbb{R}\). Số điểm cực trị của hàm số là
\(5\).
\(2\).
\(3\).
\(1\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới.
![Cho hàm số y = f( x ) có bảng biến thiên như hình dưới. Giá trị lớn nhất của hàm số đã cho trên đoạn [ - 2;4] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1754820316/1754820394-image1.png)
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 2;4} \right]\) bằng
\( - 1\).
\(10\).
\(1\).
\(8\).
Cho hàm số đa thức bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ.
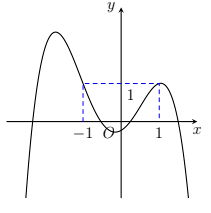
Phương trình \(f\left( x \right) - 1 = 0\) có bao nhiêu nghiệm thực phân biệt?
\(3\).
\(1\).
\(2\).
\(4\).
Đồ thị hàm số nào sau đây có hình dạng như hình vẽ?
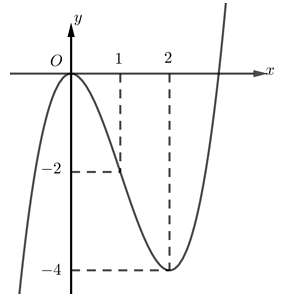
\(y = {x^3} + 3x\).
\(y = {x^3} - 3x\).
\(y = {x^3} - 3{x^2}\).
\(y = {x^3} + 3{x^2}\).
Tập nghiệm của bất phương trình \[{\left( {\frac{1}{2}} \right)^x} < \frac{1}{8}\] là
</>
\(\left( {3; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
\(\left[ {3; + \infty } \right)\).
\(\left( { - \infty ;3} \right]\).
Trong không gian \[Oxyz\], cho \[\overrightarrow a = 2\overrightarrow i - 3\overrightarrow j + \overrightarrow k \]. Toạ độ của \[\overrightarrow a \] là:
\[\left( { - 2;1;3} \right)\].
\[\left( {2; - 3;1} \right)\].
\[\left( {2;1;3} \right)\].
\[\left( {2;1; - 3} \right)\].
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội \(q = 5\). Số hạng \({u_3}\) của cấp số nhân đã cho là
\({u_3} = 50\).
\({u_3} = 12\).
\({u_3} = 10\).
\({u_3} = 7\).
Cho hình hộp \(ABCD.EFGH\).
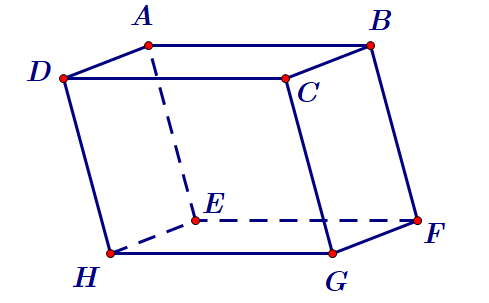
Vectơ nào sau đây bằng vectơ \(\overrightarrow {FH} \)?
\(\overrightarrow {BD} \).
\(\overrightarrow {DB} \).
\(\overrightarrow {BA} \).
\(\overrightarrow {AB} \).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, tam giác \[SAD\] đều. Góc giữa hai đường thẳng \[BC\] và \[SA\] bằng
\[60^\circ \].
\[30^\circ \].
\[90^\circ \].
\[45^\circ \].
Trong tuần lễ bảo vệ môi trường, các học sinh khối 12 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thông báo kết quả thu nhặt vỏ chai của học sinh khối 12 ở bảng sau:
|
Số vỏ chai nhựa |
\[\left[ {10,5;15,5} \right)\] |
\[\left[ {15,5;20,5} \right)\] |
\[\left[ {20,5;25,5} \right)\] |
\[\left[ {25,5;30,5} \right)\] |
\[\left[ {30,5;35,5} \right)\] |
|
Số học sinh |
\[53\] |
\[82\] |
\[48\] |
\[39\] |
\[18\] |
Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?
\[19,51\].
\[19,59\].
\[20,1\].
\[18,3\].
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x - 2}}{{x + 1}}\) là
\(y = - 2\).
\(y = 1\).
\(x = - 1\).
\(x = 2\).
